NLP-Tokenization

本章主要讲述了 NLP 的令牌化

基准：按空白字符分割

对于许多书写系统，按空白字符分割文本是一个有用的基准：

‘This isn’t an easy sentence to tokenize!’ $\Rightarrow$
[‘This’, "isn’t", ‘an’, ‘easy’, ‘sentence’, ‘to’, ‘tokenize!’]

问题：

• 我们通常希望将标点符号视为单独的标记（但仅当它们确实是标点符号时，例如 ‘U.K.’ 或 ‘10,000.00$‘）；
• 这种解决方案无法分隔没有空白字符的标记对，例如带有附加成分的表达式，如 "isn’t"。

正则表达式和语言

正则表达式

我们需要引入更复杂的模式来以上下文相关的方式描述标记边界。一种流行的解决方案是使用正则表达式（简称 regex）。

给定一个有限的 $\Sigma$ 符号字母表，$\Sigma$ 上的正则表达式及其在 $\Sigma^*$ 中的匹配通过同时递归定义如下：

1. 空字符串和 $\Sigma$ 中的任何单个符号都是 $\Sigma$ 上的正则表达式，并匹配其自身。

2. 如果 $r_1$ 和 $r_2$ 是 $\Sigma$ 上的正则表达式，那么

   1. 它们的 连接，$r_1 r_2$ 也是 $\Sigma$ 上的正则表达式，并且匹配那些恰好是匹配 $r_1$ 的字符串和匹配 $r_2$ 的字符串连接起来的字符串，且

   2. 它们的 交替，$r_1 \vert r_2$ 也是 $\Sigma$ 上的正则表达式，并且匹配那些恰好匹配 $r_1$ 或 $r_2$ 的字符串。

3. 如果 $r$ 是 $\Sigma$ 上的正则表达式，那么对 $r$ 应用 Kleene 星号 运算符，我们可以形成一个新的正则表达式 $r^*$，它恰好匹配那些由 0 个或多个匹配 $r$ 的字符串连接起来的字符串。

形式语言

给定一个有限的字母表 $\Sigma$，一个 形式语言 $\mathcal L$ 是 $\Sigma$ 上字符串的任意集合。这些字符串通常通过 语法 定义。

根据语法的复杂性，语言可以分为不同的 类型。最著名的是乔姆斯基层次结构：

• 正则语言：可以描述线性结构

  • 编程：状态机
  • 语言：单词，名词短语

• 上下文无关语言：可以描述树结构

  • 编程：XML DOM，解析树
  • 语言：短语结构语法（句子）

• 上下文相关语言：大多数人类语言是轻度上下文相关的

• 递归可枚举语言：所有可以通过算法解决的问题

回到正则表达式

一个形式语言 $\mathcal L$ 当且仅当存在一个正则表达式恰好匹配 $\mathcal L$ 的元素时，才是 正则的。

有一些简单的形式语言不是正则的，例如“孪生语言” ${ww \vert w \in {a, b}^* }$。

尽管如此，正则表达式对于许多实际任务来说已经足够灵活，并且存在高效的算法来决定字符串 $s$ 是否匹配正则表达式（时间复杂度为 $\mathcal O(\mathrm{length}(s))$）。

有限状态接受器与正则语言

有限状态接受器是消耗字符输入序列并可以“接受”或“拒绝”输入的有限状态机。它们与最简单的 FSA (有限状态自动机) 不同之处在于：

• 有一个明确的 开始状态，

• 一组指定的 接受状态，以及

• 它们的转换由有限字母表中的符号或空字符串标记。

当且仅当有限状态接受器具有从开始状态开始、在接受状态结束的转换序列，并且转换标签的连接是所讨论的输入时，它才 接受 输入。

接受单词“car”、“cars”、“cat”和“cats”的接受器：

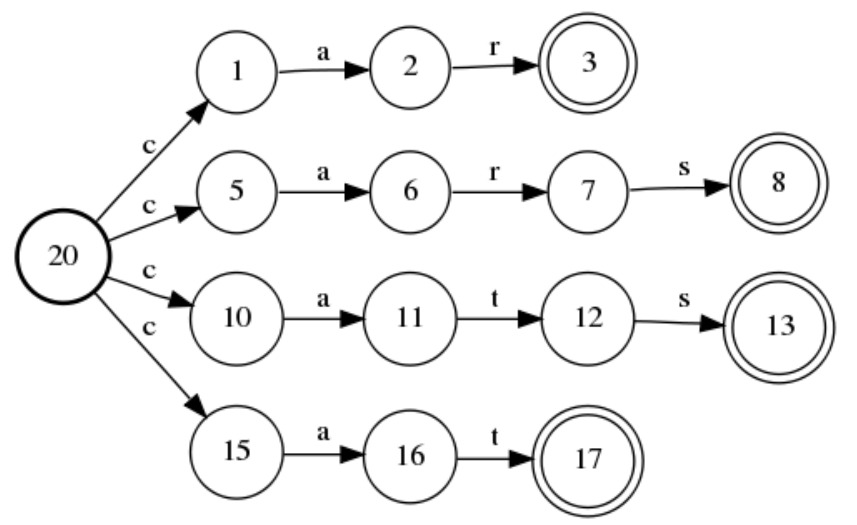
可以简化为：

有限状态接受器与 正则语言/表达式 之间的联系由 Kleene 的 等价定理 建立：

• 当且仅当存在一个 FSA 接受器恰好接受其元素时，一个语言是正则的。

这种等价性在理论和实践中都很重要：有非常高效的算法可以 简化/最小化 有限状态接受器，并决定它们是否接受一个字符串。

正则表达式：扩展

便利扩展 不增加表达能力，只是添加了一些有用的快捷方式，例如：

• 字符类匹配集合中的任何单个符号，例如 [0-9]；
• 补充字符类匹配 不在 补充集合中的任何字符，例如 [^ab]；
• 用于指定模式重复次数的运算符，例如，$r{m,n}$ 匹配 $s$ 如果 $s$ 重复 $r$ 模式 $k$ 次，其中 $m\leq k \leq n$。
• 可选匹配：$r? = r{0,1}$
• Kleene plus：$r+ \approx r{1,\infty}$

正则表达式：反向引用

所谓的 反向引用 结构，允许命名和引用与正则表达式的早期部分相对应的匹配项，从而增加了表达能力。

例如，大多数当前的正则表达式库允许类似于以下的正则表达式：

(?P<a>[ab]*)(?P=a)

它使用反向引用来定义前面提到的非正则“孪生语言”。

基于正则表达式的查找和替换

除了将整个字符串与正则表达式匹配之外，还有两个基于正则表达式的常见任务：

• 查找与正则表达式匹配的字符串子串，

• 基于正则表达式的查找和替换：在其最简单的形式中，这是用给定的字符串替换匹配的子串，但现代正则表达式库提供了两个显著的额外功能：

  • 正则表达式可以有前瞻和后顾部分，这些部分在查找匹配时使用，但不计入被替换的部分；
  • 替换不必是固定的—它们可以包含对匹配部分的反向引用。

基于规则的分词

基于正则表达式级联的分词

核心思想：对输入执行基于正则表达式的替换，最终只需按空白字符分割即可。

Penn Tree Bank 附带的 分词器 sed 脚本 是一个很好的例子。几个具有代表性的规则（\& 指代完整匹配，\n 指代第 $n$ 个组）：

• ‘...’ $\Rightarrow$ ‘ ... ‘（分隔省略号）
• [,;:#$%&] $\Rightarrow$ ‘ \& ‘（分隔各种符号）
• ([^.])([.])([])}"‘]*)[]*\ $\Rightarrow$ ‘\1 \2\3’（假设句子输入并仅分隔最终句号）
• "‘ll" $\Rightarrow$ " ‘ll"（分隔缩略词 ‘ll）

主要问题是如何正确处理例外情况：例如，单词结尾的句号应被分割，除了缩写。

标准解决方案是在执行相关替换之前，将有问题的表达式替换为无问题的占位符，例如：

(etc\. $\vert$ i\.e\. $\vert$ e\.g\.) $\Rightarrow$ <abbrev>

此解决方案需要跟踪占位符替换，并在执行有问题的规则后恢复原始内容。

基于词法分析器的解决方案

它们使用现成的“词法分析器”（lexical analyzers），最初是为计算机程序的 令牌化/词法分析 而开发的。

一个典型的词法分析器将字符流作为输入，并从中生成分类的标记流：

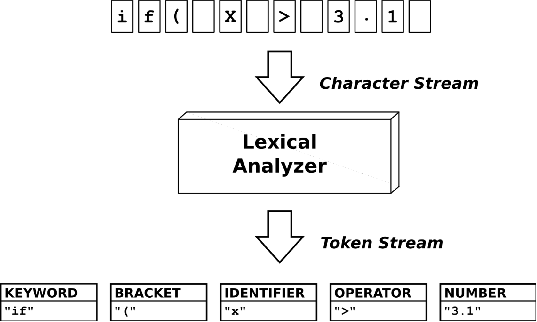
大多数词法分析器实际上是词法分析器生成器。它们的输入是标记类（类型）、正则表达式模式和

[RegexPattern] $\Rightarrow$ [Action]

规则（其中最重要的操作是将实际匹配分类为给定类型的标记），并生成一个具体的、优化的词法分析器来执行给定的规则，例如通过生成分析器的 C 源代码。

SpaCy 的基于规则的分词器

1. 输入文本按空白字符分割。

2. 然后，分词器从左到右处理文本。对于每个子字符串，它执行两个检查：

   1. 子字符串是否匹配分词器异常规则？例如，“don’t”不包含空白字符，但应被分割。

   2. 前缀、后缀或中缀是否可以被分割？例如，逗号、句号等标点符号。

      如果有匹配，则应用规则，分词器继续循环，从新分割的子字符串开始。

一个简单的例子：对 “Let’s go to N.Y.!” 进行分词

编辑距离

除了将输入分割成单元外，分词还涉及将标记分类为类型，例如决定哪些类型

‘Apple’, ‘apple’, ‘appple’

属于。在许多情况下，这些决策需要字符串之间的相似性度量。

在这个领域中，最重要的度量家族之一是所谓的 编辑距离 家族，它通过将两个字符串相互转换所需的最少编辑操作次数来衡量它们之间的距离。

给定

• 一组 编辑操作（例如，从字符串中删除或插入一个字符），以及
• 一个 权重函数，它为每个操作分配一个权重，

两个字符串之间的 编辑距离（一个源字符串和一个目标字符串）是将源字符串转换为目标字符串所需的最小总权重。

Levenshtein 距离

最重要的变体之一是所谓的 Levenshtein 距离，其中操作是

• 删除，
• 插入，和
• 替换字符

且所有操作的权重均为 1.0。

子词分词

分词 与 子词分词

经典的分词旨在将输入字符流精确地分割成语言学上有意义的单元：单词和标点符号。

这种类型的分词对于人类语言分析很有用，但对于构建大型语言模型却不适用，因为它

• 相当具有挑战性，因为存在各种书写系统和语言，它们都需要（有时是根本不同的）规则/模型

• 在较大的语料库上会生成巨大的词汇表，并且仍然会导致词汇外单词的问题

一种最近开发的替代方法是 subword tokenization。许多现代的深度端到端 NLP 架构使用子词分词而不是经典分词来分割输入。其主要优点是：

• 需要很少或几乎不需要预分词
• 统计和数据驱动：从语料库中学习分割模型（无需手动编写规则）
• 词汇表大小可以自由选择；它将包含最常见的单词和子词单元
• 与书写和语言无关

这对文本意味着：

• 输入文本将被分割成最常见的单词和子词
• 分割质量取决于词汇表大小
  • 对于单一语言，30,000 个类型就足够了
  • 一个常规的词汇表通常有几十万甚至几百万个类型
• 没有词汇外单词（在正确设置下！）
• 子词片段通常是有信息量的，边界经常接近形态学（morphological）边界

字节对编码 (BPE)

Byte Pair Encoding 最初是一种用于字节序列的简单压缩技术，但可以推广到由有限字母表中的符号组成的任何序列。为了生成字母表上的序列的 编码/压缩 版本，

1. 用字母表中的符号初始化符号列表，并且

2. 反复计算所有符号对，并用新的 ‘AB’ 元素替换每个最频繁对 (‘A’, ‘B’) 的出现，并将 ‘AB’ 添加到符号列表中

这种技术如何用于文本的子词分词？诀窍是通过对文本应用 BPE，从训练语料库中学习用于分割的词汇。修改如下：

• 从粗略的预分词开始（通常非常简单，例如按空白字符分割）
• 不允许 BPE 合并跨越单词边界。

在实践中，这些修改通常通过向字母表中添加一个新的 ‘_‘ 单词起始（或单词结束）符号来实现，并规定 ‘_‘ 只能结束（或开始）合并项。

一个简单的例子：在不同数量的合并操作后，句子的 BPE 编码版本。

随着合并次数的增加，越来越多的符号变成完整的单词。

贪婪 BPE 子词分词

使用 BPE 处理语料库会产生

• 一个包含所有字符及其合并结果的 词汇表
• 以及按执行顺序排列的 合并列表

然后，通过按照合并列表中的顺序执行所有适用的合并，对新的预分词输入进行子词分词。

WordPiece

WordPiece 是一种子词分词方法，与 BPE 只有略微不同。不同之处在于：

• 合并 AB 对是那些具有最高值的对 $\frac{freq(AB)}{freq(A) \times freq(B)}$，其中 $freq(\cdot)$ 是训练语料库中类型的频率
• 使用生成的词汇进行分词时，使用 MaxMatch 算法：

子词采样

BPE 和 WordPiece 的默认子词分词策略会确定性地生成单词的贪婪匹配分解，即使存在有信息的替代分割：

unrelated = unrelate + d

unrelated = un + related

为了解决这个问题，开发了从可能的替代分解中概率采样的解决方案。

• BPE dropout 在分词过程中随机丢弃一些 BPE 合并规则，而
• Unigram 语言模型 基于一种新颖的概率子词分词方法，该方法从启发式估计的最优词汇表的超集开始，并递归地删除对构建训练语料库的简单（单项）概率语言模型最不有用的条目。

与 BPE 相比，递归 Unigram 语言模型词汇构建步骤的概率性质使得可以为替代分割分配合理的概率，并从中进行采样。

SentencePiece

在其原始形式中，BPE 和 WordPiece 需要（粗略的）预分词作为预处理步骤。与此相反，SentencePiece 分词器库能够以相同的方式处理每个字符，甚至包括空格，并且可以将 BPE 或单项语言模型方法应用于原始句子甚至段落，从而消除了预分词的需要。

因此，SentencePiece 是从原始文本生成深度端到端模型输入的最流行解决方案之一。