NLP-NGram-LM
基于 N-gram 的语言模型
语言模型
什么是语言模型?
回想一下,在形式语言理论中,语言 $\mathcal L$ 只是某个字母表 $\Sigma$ 的子集 $\Sigma^*$。
相反,统计语言模型切换到语言生成的概率视图,并为来自词汇 $V$ 的任意序列 $\langle w_1,\dots, w_n\rangle \in V^*$ 分配一个概率
$$P(\langle w_1,\dots, w_n\rangle)$$
使得
$$\sum_{\mathbf{w}\in V^*} P(\mathbf{w}) = 1$$
词汇表
传统上,语言模型的词汇表由完整的单词组成,例如,
$V$ = {the, be, to, of, $\dots$}
但最近基于子词和字符的语言模型也被广泛使用,词汇表如
{ _don’, t, _un, related, $\dots$} 或 {a, b, c, d, e, f, $\dots$}
本章讨论基于单词的语言建模技术 — 字符和子词级别建模技术将是第 9 和第 11 讲的主题。
为什么语言模型有用?
概率语言模型对于大量的自然语言处理应用非常重要,其目标是生成合理的词序列作为输出,其中包括
拼写和语法检查
预测输入
语音转文字
聊天机器人
机器翻译
摘要生成
使用连续概率建模
使用链式法则,令token序列 $\mathbf{w} = \langle w_1,\dots, w_n\rangle$ 的概率可以重写为
$$P(\mathbf w)= P(w_1)\cdot P(w_2 \vert w_1 )\dots \cdot P(w_n\vert w_1,\dots, w_{n-1})$$
也就是说,对于一个完整的语言模型,只需指定
- 对于任何 $w\in V$ 单词,概率 $P(w)$ 表示它将是序列中的第一个单词,以及
- 对于任何 $w\in V$ 和 $\langle w_1,\dots,w_n\rangle$ 部分序列,单词 $w$ 的连续概率,即
$$P(w ~\vert ~ w_1,\dots,w_n)$$
起始和结束符号
基于链式法则的序列概率公式
需要一个单独的、无条件的子句来表示起始概率,并且
没有解决在某个点结束序列的概率。
这两个问题都可以通过在词汇表中添加显式的 $\langle start \rangle$ 和 $\langle end \rangle$ 符号来解决,并假设语言的所有序列都以这些符号 开始/结束。通过这个技巧,起始/结束 概率可以重写为条件形式 $P(w \vert \langle start \rangle)$ 和 $P(\langle end \rangle \vert \mathbf{w})$
语言模型树结构
使用 起始/结束 符号,语言模型分配的词序列及其连续概率可以排列成树结构:
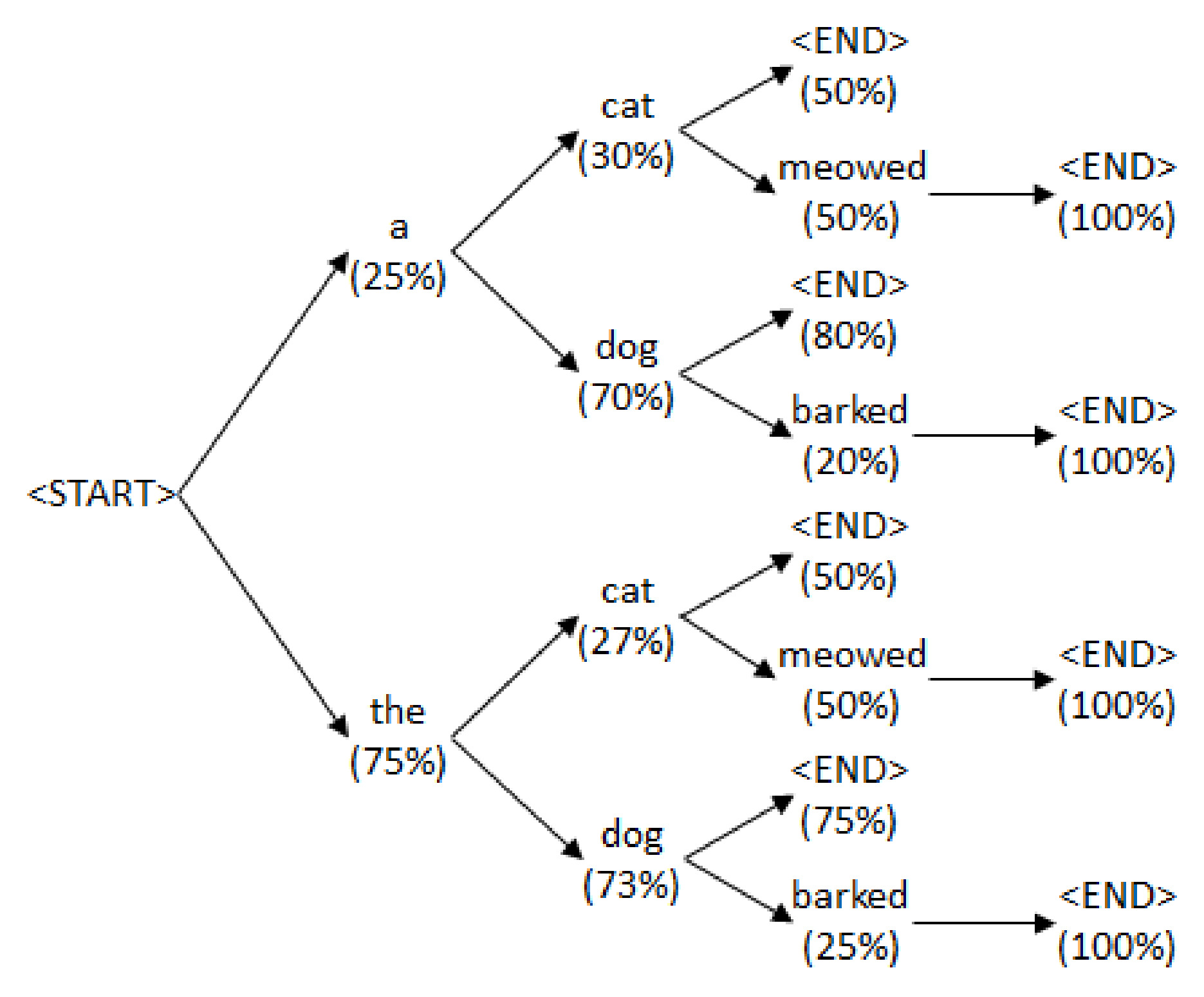
文本生成
使用语言模型,可以基于模型的生成概率分布生成新的文本。
在前一张幻灯片所示的树结构中,我们寻找权重(对数概率)之和较大的分支。穷举搜索是不可行的,众所周知的策略包括
贪婪搜索
集束(beam)搜索
随机集束搜索
一个简单的集束搜索示例,$K=5$:
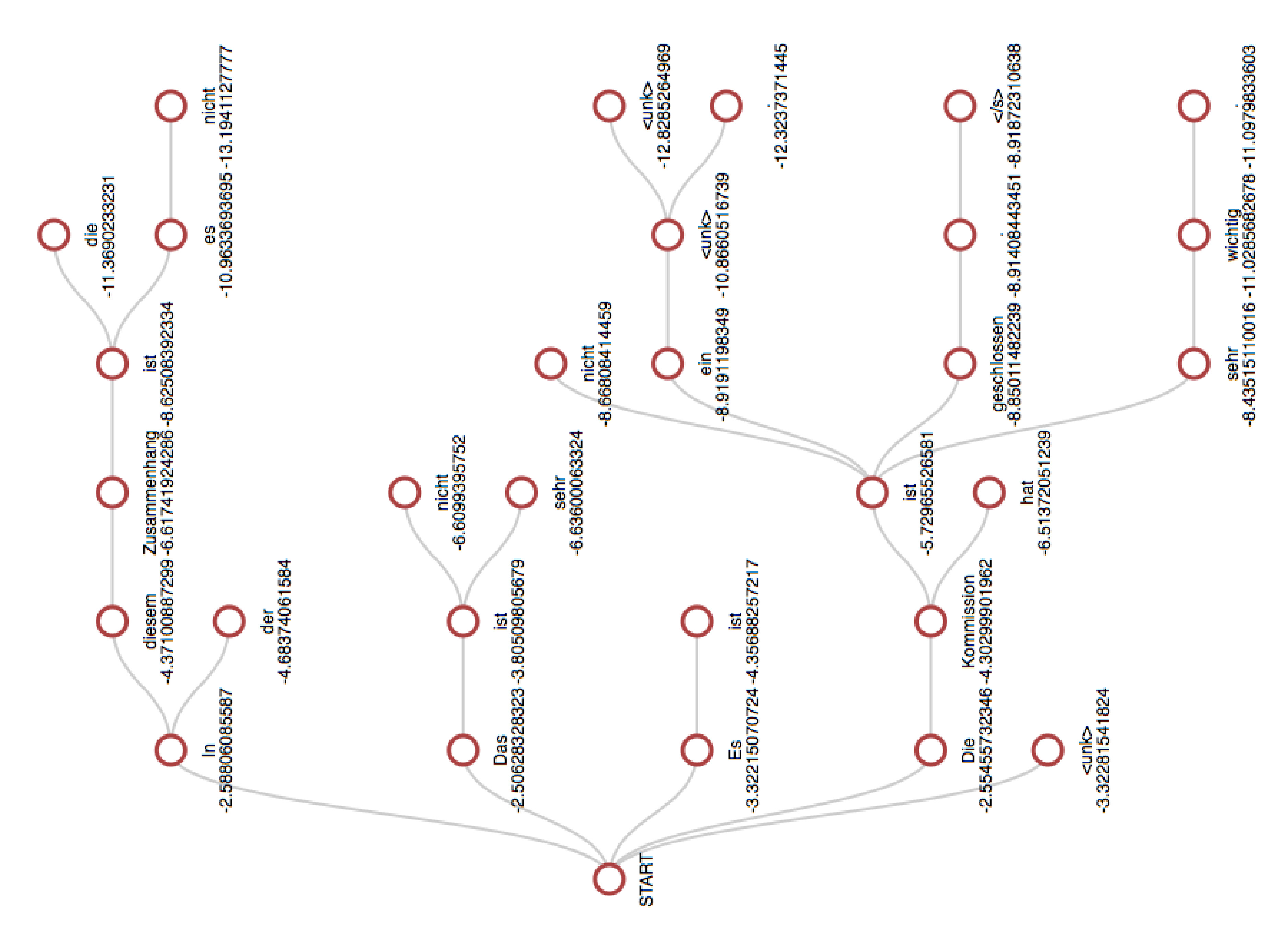
评估
语言模型的评估可以是
外在的: extrinsic,模型在拼写检查、语音转文字系统等组件中的表现如何,或者
内在的: intrinsic,分配的概率与测试语料库中的文本对应得有多好?
最广泛使用的内在评估指标是语料库的 困惑度。
语言模型 $\mathcal M$ 在序列 $\mathbf w = \langle w_1,\dots, w_n\rangle$ 上的困惑度为
使用链式法则,困惑度可以重写为
$${\sqrt[n]{\frac{1}{P_{\mathcal M}(w_1)}\cdot \frac{1}{P_{\mathcal M}(w_2 \vert w_1 )}\dots\cdot \frac{1}{P_{\mathcal M}(w_n\vert w_1,\dots, w_{n-1})}}}$$
这正是语料库中所有单词条件概率倒数的几何平均值。
换句话说,困惑度衡量的是,对于语言模型来说,语料库中的单词(续词)平均而言有多“出乎意料”。
取困惑度的对数,通过一些简单的代数运算可以得到结果
$$-\frac{1}{n} \left(\log P_{\mathcal M}(w_1) + \sum_{i=2}^n\log P_{\mathcal M}(w_i \vert w_1,\dots, w_{i-1})\right)$$
这就是每个单词的平均交叉熵和负对数似然。
一个简单的推论是:通过最小化平均交叉熵(cross-entropy)或最大化平均对数似然(log-likelihood),也可以最小化模型在训练数据上的困惑度(perplexity)。
基于 N-gram 的建模
概率估计
我们如何从文本语料库中估计所需的 $P(\mathbf{w})$ 概率?我们可以尝试使用出现次数来获得最大似然估计:
$$P(\mathbf{w}) \approx \frac{C(\mathbf{w})}{C(\mathrm{all \space texts \space in \space corpus})}$$
但在任何现实的语料库中,大多数文本只出现一次,许多可能的文本根本没有出现。一个选项是切换到连续概率:
$$P(w_{i} \vert w_1,\dots,w_{i-1})$$
使用基于计数的估计,我们可以得到
$$P(w_{i} \vert w_1,\dots,w_{i-1}) \approx \frac{C(\langle w_1,\dots,w_{i} \rangle)}{C(\langle w_1,\dots,w_{i-1} \rangle)}$$
但同样会遇到数据稀疏性问题。缓解这一问题的一种方法是使用
$$P(w_{i} \vert w_1,\dots,w_{i-1}) \approx P(w_{i} \vert w_{i-k},\dots,w_{i-1})$$
的近似,对于某个 $k$,假设续词概率(近似)由序列中前 $k$ 个 token 决定。
N-gram 语言模型
使用这种近似,$\langle w_1,\dots,w_n \rangle$ 序列的概率可以计算为
$$P(w_1) \prod_{i=2}^k P(w_{i} \vert w_{1},\dots,w_{i-1}) \prod_{i=k+1}^n P(w_{i} \vert w_{i-k},\dots,w_{i-1})$$
其主要优点是
$$P(w_{i} \vert w_{i-k},\dots,w_{i-1}) \approx
\frac{C(\langle w_{i-k},\dots,w_{i}\rangle)}{C(\langle w_{i-k},\dots,w_{i-1} \rangle)}$$
的估计可以仅基于语料库中最长为 $k+1$ 的子序列计数,即所谓的 N-gram $(N=1, 2, 3,\dots)$
一元模型
最简单的 $N$-gram 语言模型是*一元(Unigram)*模型,它为序列 $\langle w_1,\dots,w_n \rangle$ 分配概率
$$P(w_1)\cdot P(w_2)\cdot \dots \cdot P(w_{n-1})\cdot P(w_n)$$
其中单词概率可以简单地估计为
$$P(w) \approx \frac{C(w)}{\sum_{w’ \in V}C(w’)}$$
一元模型忽略了单词的顺序,最可能的序列只是完全由最频繁的单词组成的序列。
二元模型
自然地,基于更长子序列的 $N$-gram 模型更加细致,甚至所谓的*二元(Bigram)*模型($N=2$)计算序列概率简单为
$$P(\langle w_1,\dots,w_n \rangle) = P(w_1)\prod_{i=2}^n P(w_i \vert w_{i-1})$$
其中
$$P(w_2 \vert w_1) \approx \frac{C(\langle w_1,w_2\rangle)}{C(w_1)}$$
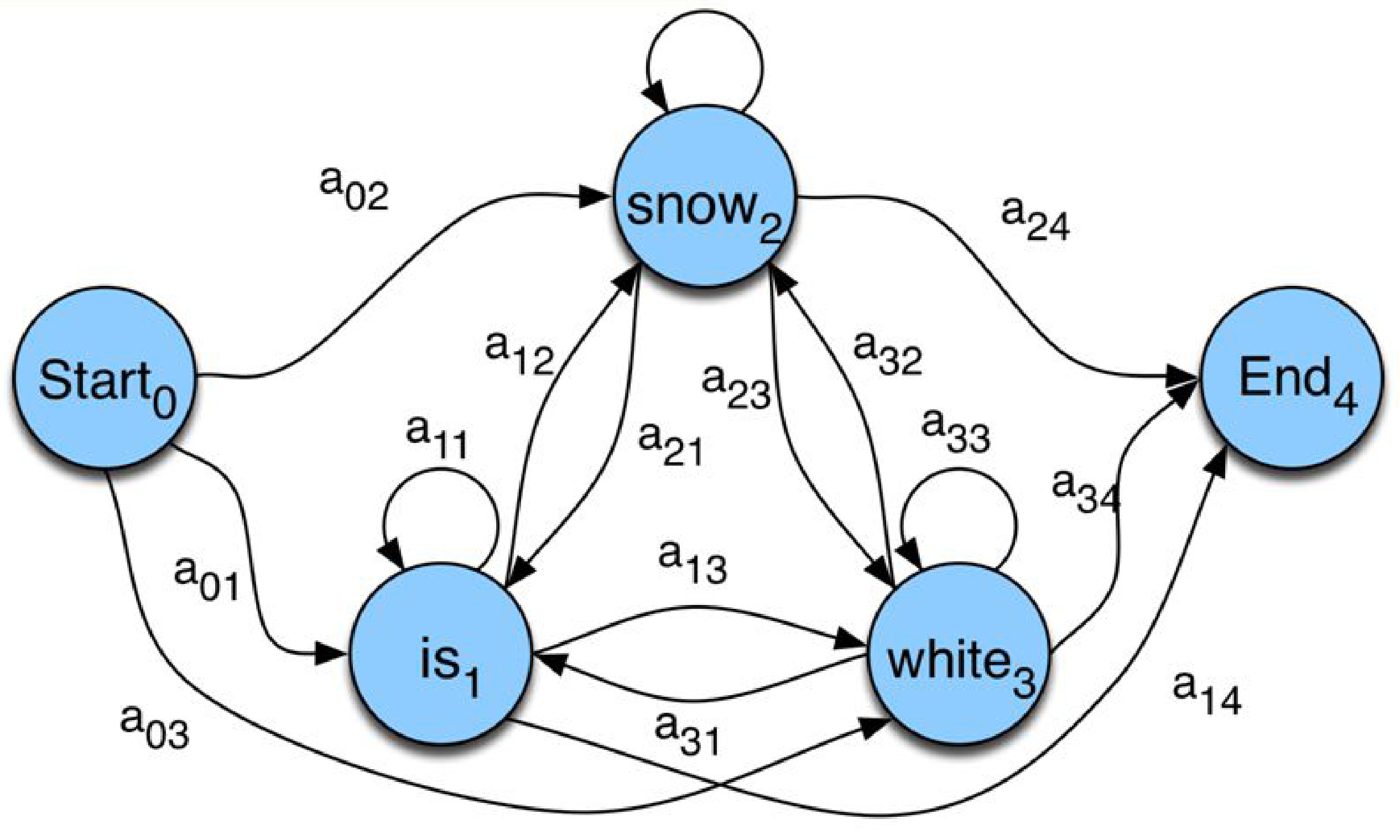
马尔可夫语言模型
$N$-gram 模型实际上是用概率有限状态机(Markov)来建模语言,其中状态对应于 $N-1$-gram。
例如,在 $\mathcal M$ 二元模型的情况下,状态对应于词汇表加上一个开始和结束状态,状态 $w_1$ 和 $w_2$ 之间的转移概率只是 $P(w_2 \vert w_1)$ 的续词概率。
很容易看出,token 序列 $\mathbf{w}=\langle w_1,\dots,w_n \rangle$ 的 $P_\mathcal{M}(\mathbf{w})$ 概率正是马尔可夫模型经过状态 $\langle start \rangle,w_1,\dots,w_n,\langle end \rangle$ 的概率。
一个简单的马尔可夫语言模型:
增加 N 值
由于实际上人类语言过于复杂,无法满足低阶马尔可夫假设,因此具有更高 N 值(如 N=3,4 甚至 5)的 N-gram 模型通常具有更好的内在和外在性能。不幸的是,随着 N 的增加,语言学上可能的 N-gram 数量急剧增加。例如,在谷歌的 1,024,908,267,229 token 的 N-gram 语料库 中,N-gram 计数为:
- 一元模型:13,588,391
- 二元模型:314,843,401
- 三元模型:977,069,902
- 四元模型:1,313,818,354
- 五元模型:1,176,470,663
对于较高 $N$ 值,语言学上可能的 $N$-gram 数量极高,这带来了两个重要问题:
数据稀疏性: 即使在大型文本语料库中,许多可能的组合也不会出现,或者只会很少出现,因此很难估计它们的概率;
模型大小: 即使估计是正确的,模型的大小也会非常庞大。
平滑
加法平滑
Additive smoothing。我们如何解决在语料库中从未或很少出现的 $N$-gram 的问题?一个简单的解决方案是通过某个数值过度计数每个 $N$-gram,并使用
$$P(w_{i} \vert w_{i-k},\dots,w_{i-1}) \approx \frac{C(\langle w_{i-k},\dots,w_{i}\rangle)+\delta}{C(\langle w_{i-k},\dots,w_{i-1} \rangle) + \delta|V|}$$
$|V|$ 乘数来自于这样一个事实:对于每个 $N-1$-gram,恰好有 $|V|$ 个 $N$-gram 是它的延续。
$\delta$ 的一个广泛选择是 1。
一个重要的问题是:
如果 $C(\langle w_1,w_2\rangle)=0$ 和 $C(\langle w_1,w_3\rangle)=0$,那么在加法平滑下我们有
$$p(w_1,w_2)=p(w_1,w_3)$$
假设现在 $w_2$ 比 $w_3$ 常见得多。那么,直观上,我们应该有
$$p(w_1,w_2)>p(w_1,w_3)$$
而不是上述的相等关系,因此加法平滑的结果似乎是错误的—我们应该以某种方式在一元和二元计数之间进行插值。
插值
Interpolation,在二元模型的情况下,我们通过一定的权重添加来自一元模型频率的概率:
$$P(w_2 \vert w_1) \approx \lambda_1\frac{C(\langle w_1, w_2 \rangle)}{C(w_1)} + (1 - \lambda_1)\frac{C(w_2)}{\sum_{w\in V}C(w)}$$
对于任意 $k$ 的递归解决方案:
$$P(w_{k+1} \vert w_1.. w_k) \approx \lambda_k\frac{c(\langle w_1 .. w_{k+1} \rangle)}{c(\langle w_1 .. w_k\rangle)} + (1-\lambda_k)P(w_{k+1} \vert w_2 .. w_{k})$$
$\lambda_k$ 是基于语料库经验设置的,通常使用期望最大化(Expectation Maximization)方法。
NLP-NGram-LM