NLP-Classification-SequenceTagging

分类和序列标注

文本分类

文本分类任务

文本分类任务是从给定的 $C={c_1,\dots,c_n}$ 类别/分类标签集中为 $d$ 文本/文档 分配适当的标签。

代表性的例子包括

• 情感分析：根据文档表达的情感进行分类。标签集示例：

  • { positive, negative, ambigous }
  • { admiration, amusement, annoyance, approval, …, sadness, surprise }

• 垃圾邮件检测：SPAM，二分类决定消息是否为未经请求的邮件

• 作者身份检测：从指定的作者集中确定谁写了文本

• 作者特征检测：作者是男性还是女性，他们的年龄等

• 主题/话题检测：文档属于预定义列表中的哪个 主题/话题，例如，在国会图书馆分类系统中 { 医学, 农业, 科学, 美术, … }

• 体裁检测：Genre，确定文本的体裁，例如，从集合 { 科幻, 冒险, 爱情故事, 悬疑, 历史, 西部 } 中分配标签

方法

• 手工设计的基于规则的系统：例如，使用精心设计的与类别正相关或负相关的词列表。

这些系统可以达到良好的性能，但需要大量的手工工作，并且难以维护和适应。

• 机器学习方法：在包含标记文档的监督数据集上学习的模型：
  ${\langle d_i, c_i \rangle}_{i\in {1, \dots, N}}$

  方法范围从线性机器学习方法如逻辑回归（logistic regression）到深度神经网络。

词袋表示法

Bag of words

许多基于机器学习的分类方法需要将输入表示为固定长度的数值向量。对于长度不一的文本，一个常见的方法是使用词袋表示法：

• 使用词汇表 $V={w_1,\dots,w_N}$ 对输入文本进行分词
• 并将它们表示为 $|V|=N$ 维的词频向量，即，对于一个文档 $d$，$BOW_V(d)=\langle c_{1,d}, \dots, c_{N,d}\rangle$，其中每个 $c_{i,d}$ 是 $w_i$ 在 $d$ 中的出现次数

一个简单的例子：

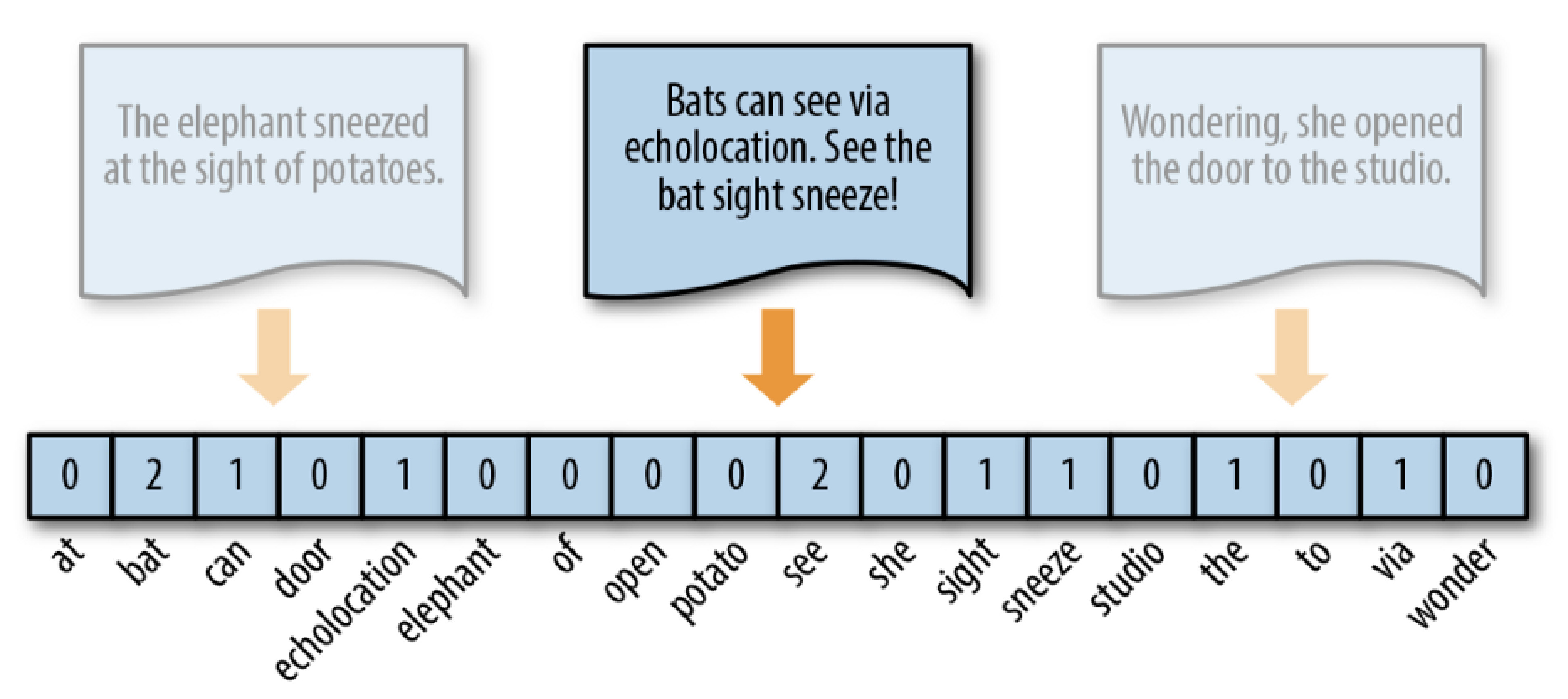
词袋表示法的改进

基本的 BOW 表示法可以通过几种方式进行改进，可能最重要的三种是：

• 从 BOW 向量中省略stopword（非信息词）的计数。什么算作停用词取决于任务和领域，但通常会考虑（某些）功能词，例如限定词作为停用词
• 向 BOW 表示中添加一些词序列计数，例如，bigram或三元组计数
• 根据词的信息量对词进行加权：最广泛使用的方法是根据词频和逆文档频率（term frequency-inverse document frequency）进行加权

TF-IDF 方案

TF-IDF 加权方案的基本假设是，出现在大部分训练文档中的词不如只出现在少数文档中的词信息量大。因此，TF-IDF 向量相应地通过文档频率来折扣 word counts（term frequencies）。一个简单但广泛使用的变体：

$$TF{\text -}IDF(d)=\langle tf_{1,d}\cdot idf_1, \dots, tf_{N,d}\cdot idf_N\rangle$$

其中 $tf_{i,d}$ 只是 $w_i$ 在 $d$ 中的出现次数，而

$$idf_i = \log\frac{\mathrm{\# of \space all \space documents}}{\mathrm{\# of \space documents \space containing} \space w_i }$$

二进制词袋表示法

词袋表示法的一种有趣的简化是仅指示单词的存在或不存在：

$$BOW_{bin}(d)=\mathop{\mathrm{sign}}(BOW(d))$$

其中 $\mathop{\mathrm{sign}}$ 函数的应用是逐元素的，即，

$$BOW_{bin}(d)=\langle \mathop{\mathrm{sign}}(c_{1,d}), \dots, \mathop{\mathrm{sign}}(c_{N,d})\rangle$$

事实证明，在许多情况下，这些更简单且占用内存更少的表示法可以代替正常的 BOW 向量使用，而不会有明显的性能差异。

朴素贝叶斯与词袋表示法

Naive Bayes classifier with BOW

在其最简单的形式中，朴素贝叶斯（NB）分类器是一种生成模型，建模 $\mathbf{x}$ 观测特征向量和它们的 $c$ 类别标签的联合分布为

$$P(\mathbf{x}, c) = P(c)\prod_{i=1}^D P(x_i \space \vert \space c)$$

该模型被称为“朴素”，因为它基于条件独立假设（conditional
independence assumption），即在给定类别标签的情况下，所有观测特征彼此独立。

NB 模型可以通过指定以下内容来精确描述：

• 类别标签的分类分布 $P(c)$，以及
• 每个 $x_i$ 观测特征和 $c_j$ 标签的 $P(x_i \space \vert \space c_j)$ 分布

$P(c)$ 始终是一个分类（伯努利或“多项”）分布，而 $P(x_i \space \vert \space c_j)$ 分布的选择取决于 $x_i$ 的类型；对于连续的 $x_i$，它可以是任何连续分布，高斯分布是一个常见的选择。

NB 模型可以通过将 NB 假设应用于单个标记来适应文本分类：假设每个标记是根据分类条件分布 $P(w \space | \space c)$ 独立选择的。如果 $\mathbf{x}$ 是一个词袋向量，$c$ 是一个类别标签，这意味着

$$P(\mathbf{x}, c) = P(c) \prod_{i=1}^{|V|}P(w_i \space \vert \space c)^{x_i}$$

为了数值稳定性，对两边取对数：

$$\log P(\mathbf{x}, c) = \log P(c) + \sum_{i=1}^{|V|}x_i \log P(w_i \space \vert \space c)$$

这意味着，给定一个 $\mathbf{x}$ 词袋向量和一个向量

$$\theta_c=\langle \log P(w_1 \space \vert \space c),\dots,\log P(w_{|V|} \space \vert \space c) \rangle$$

表示类别 $c$ 的条件对数概率，

$$\log P(\mathbf{x}, c) = \log P(c) + \theta_c \cdot \mathbf{x}$$

即 $(\mathbf{x}, c)$ 的对数概率对于每个 $c_i$ 是一个简单的线性函数。对于一个文档 $d$，预测最可能的类别也非常简单：

$$\hat c = \mathop{\mathrm{argmax}}_{c\in C}(\log P(c) + \theta_{c} \cdot BOW(d))$$

模型参数的最大似然估计可以基于简单的计数：

$$P(c) \approx \frac{\# \mathrm{of} \space c \space \mathrm{documents}}{ \# \mathrm{of \space all \space documents }}$$

$$P(w \space | \space c) \approx \frac{\# w \space \mathrm{occurrences \space in} \space c \space \mathrm{documents}}{\# of \space \mathrm{words \space in} \space c \space \mathrm{documents}}$$

由于我们基本上在处理每个类别的（unigram）语言模型，数据稀疏性再次带来了问题。

最极端的情况是，如果一个词 $w\in V$ 在任何 $c$ 类别的文档中都没有出现，那么基于语料库的最大似然估计 $P(w \space | \space c)=0$，因此，对于任何包含 $w$ 的非零计数的 $\mathbf{x}$ 词袋向量的文档，

$$P(\mathbf{x}, c) = P(c) \prod_{i=1}^{|V|}P(w_i \space \vert \space c)^{x_i}=0$$

无论它们包含任何其他词。

解决方案是使用适当的平滑方法，例如，加一平滑。

朴素贝叶斯的局限性

尽管基于 BOW 的 NB 模型相对简单，可以用于估计和预测，并且表现尚可，但也存在一些缺点：

• NB 条件独立假设相当不现实，并且在基本 BOW 模型中会导致误导性的概率预测
• NB 假设使得使用 $N$-gram 基于 BOW 的特征向量比使用 unigram 更加值得怀疑
• 对于判别任务使用完整的生成模型通常会带来一些性能损失

判别线性方法

在经典学习算法领域中，最重要的替代方法是使用 BOW 向量的判别方法之一：

• 感知器变体 perceptron variant
• 逻辑回归
• 支持向量机（SVM），
• 基于决策树的集成方法，如随机森林或梯度提升树

这些模型不假设条件独立，并且在使用改进的（例如基于 $N$-gram 的）BOW 表示作为输入时没有问题。

有些出乎意料的是，在某些应用中，在朴素贝叶斯文本分类器中使用重叠(overlapping)的 $N$-gram 实际上对性能有益处，例如，character $N$-gram 经常用于语言识别的 NB 模型中。

序列标注

序列标注任务通常是将给定有限标签集 $T$ 中的一个标签分配给可变长度输入序列的每个元素。在 NLP 中，输入序列通常是 $\langle w_1,\dots,w_n \rangle$ 的标记序列。因此，序列标注任务也被称为 标记分类。

在传统的 NLP 流水线中，有些任务是明确的序列标注任务，例如词性标注（POS-tagging）和形态标注（morphological tagging）。其他任务，如名词短语分块（NP-chunking）、命名实体识别（NER）或关键词识别，可以通过简单的技巧转化为序列标注任务。

IOB 标注

Inside-Outside-Beginning

这些任务表面上是跨度查找和跨度标注任务：目标是找到属于某些类别的标记跨度。

例如，在（最小）名词短语（NP）分块的情况下：

IOB 技巧是将 跨度识别/标注 （span identification） 任务重新表述为序列标注任务。如果有 $T_1,\dots,T_N$ 个要识别的跨度类型，那么我们引入三种类型的标记级别标签：

• 对于所有跨度类型的 $B$（开始）标签：
  $BT_1,\dots,BT_N$ 表示给定类型的跨度的第一个标记

• 对于所有跨度类型的 $I$（内部）标签：
  $IT_1,\dots,IT_N$ 表示一个标记在跨度内（作为第二个或更晚的元素），最后

• 对于不属于任何要找到的跨度类型的标记，使用唯一的 $O$ 标签

使用这些标签，跨度识别任务变成了序列标注任务。

除了 IOB（BIO）之外，还有其他方案，最流行的是 BIOES，它引入了 $ET_i$ 结束标签，以及用于单标记跨度的 $ST_i$ 标签。

序列标注的挑战

序列标注的主要挑战是元素标签与其他元素的特征（包括它们的标签）之间的复杂相互依赖性：在大多数 NLP 标注任务中，标签是 强烈依赖上下文 的。

另一个重要问题是特征工程：哪些序列元素的特征与标注相关？如果要正确处理词汇表外的单词，那么至少有些特征可能应该基于单词的表面形式，例如其大写、后缀等。

序列标注的监督方法

这些方法假设有一个监督数据集

$$D={\langle \mathbf{x_1},\mathbf{y_1} \rangle,\dots, \langle \mathbf{x_N},\mathbf{y_N} \rangle}$$

其中每对 $\langle \mathbf{x}_i, \mathbf{y}_i \rangle$ 包含一个要标注的序列 $\langle x_1^i,\dots,x_{n_i}^i\rangle$ 和对应的正确标签序列 $\langle y_1^i,\dots,y_{n_i}^i\rangle$。

我们将讨论的方法都是概率方法（probabilistic）：它们要么建模 $P(\mathbf{X}, \mathbf{Y})$ 联合分布（generative model），要么建模 $P(\mathbf{Y} \space | \space \mathbf{X})$ 条件分布（判别模型，discriminative model）。

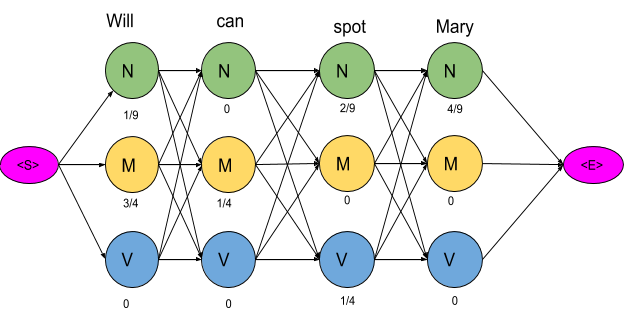
隐马尔可夫模型

(Hidden Markov models) HMMs 是基于假设可观察序列 $\mathbf{x}$ 的元素实际上依赖于位置上对应的隐藏序列 $\mathbf{y}$ 的元素的 $P(\mathbf{X}, \mathbf{Y})$ 分布的生成模型，而这些隐藏元素又根据马尔可夫模型分布。条件独立假设共同遵循以下图形模型：

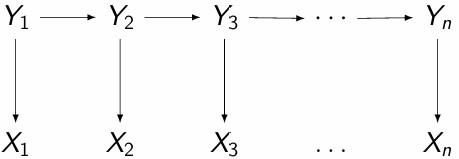
由于关于 $Y$ 的马尔可夫模型假设，有一个 $A$ 矩阵指定所有标签的转移概率，因此对于任何适当的 $k, i, j$，

$$P(Y_k=y_j \space | \space Y_{k-1}=y_i) = a_{i j}$$

HMMs 还假设 $P(X \space | \space Y)$ 发射概率与位置无关：因此也有一个 $B$ 矩阵，对于任何 $k, i, j$，

$$P(X_k= x_j \space | \space Y_{k}= y_i) = b_{i j}$$

假设最终有一个包含每个可能 $y_i$ 标签的起始概率的 $\Pi$ 向量：

$$P(Y_1 = y_i) = \pi_i,$$

具体的 $\langle \mathbf{x}, \mathbf{y} \rangle =\langle \langle x_{l_1},\dots,x_{l_n} \rangle, \langle y_{m_1},\dots,y_{m_n} \rangle \rangle$ 对的概率可以计算为

$$P(\mathbf{x}, \mathbf{y}) = \pi_{m_1} b_{m_1 l_1} \prod_{i=2}^na_{m_{i-1} m_i}b_{m_i l_i}.$$

$A, B$ 和 $\Pi$ 中概率的最大似然估计 (MLE) 可以通过简单计数来计算。如果训练数据集包含 $N$ 个序列，那么

$$ \begin{equation} \begin{gathered} \pi_i = \frac{C(\mathrm{first~~element~~is~~} y_i)}{N}\\ \nonumber a_{ij} = \frac{C(\langle y_i,y_j\rangle)}{\sum_kC(\langle y_i,y_k\rangle)}\\ \nonumber b_{ij} = \frac{C(y_i \mathrm{~~emits~~} x_j)}{C(y_i)} \nonumber \end{gathered} \end{equation} $$

与其他基于计数的 MLE 方法类似，在数据稀疏（sparse）的情况下可能需要平滑处理。

维特比算法

Viterbi algorithm

给定一个训练好的 HMM 及其 $\pi, A, B$ 参数，以及一个长度为 $n$ 的输入序列 $\mathbf{x}$，我们希望确定最可能的对应标签序列 $\mathbf{y}$，即找到

$$\mathop{\mathrm{argmax}}_{\mathbf{y}\in Y^n} P(\mathbf{y} | \mathbf{x}, \Pi, A, B)$$

这等价于

$$\mathop{\mathrm{argmax}}_{\mathbf{y}\in Y^n} P(\mathbf{x}, \mathbf{y} | \Pi, A, B)$$

穷举搜索是不可行的，因为有 $|Y|^n$ 种可能的标签序列。

动机：最小和算法

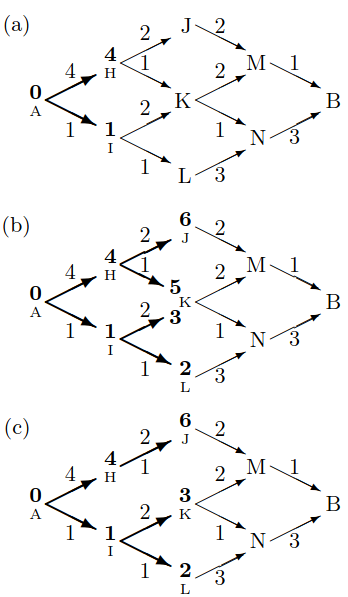
我们如何根据如下图所示的图表找到 A 和 B 之间的最低成本路径？

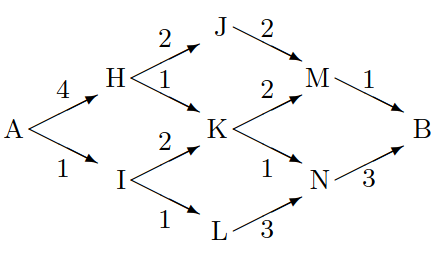
与时间复杂度可能是 A 和 B 之间最短路径长度的指数级的暴力（brute）解决方案不同，我们可以使用一个简单的 消息传递 方法。

从 A 开始，每个节点

• 接收来自其前驱节点（predecessors）的关于它们从 A 的最小和距离的消息
• 基于这些消息，计算自己的最小和距离和入边，并
• 将其最小和距离发送给所有后继节点

最终，消息到达 B，B 能够计算出 A-B 的最小和距离，并且可以重建 A 和 B 之间的最小和路径。

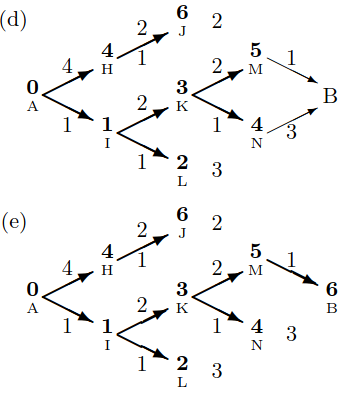
Min-Sum 算法可以适应解决我们的问题，因为它可以在不进行任何显著更改的情况下用于最大化节点之间路径上的乘积（max-product），并且 HMM 的 transition/emission 概率具有所需的有向无环图结构：

The Viterbi algorithm

更正式地说，HMM 的 conditional independence assumptions 有以下结果：如果我们知道，对于所有 $y_i\in Y$，值

$$ \mathbf{y}^{n-1}_i = \mathop{\mathrm{argmax}}_{\mathbf{y}\in Y^{n-1}~\wedge~\mathbf{y}[n-1] = y_i} P(\mathbf{x}[1:n-1], \mathbf{y} ~|~ \Pi, A, B) $$

（即以 $y_i$ 结尾的最可能的 $n-1$ 长度标签序列），那么最可能的 $\mathbf{y}$ 可以通过仅比较 $|Y|^2$ 个延续来计算：

$$ \mathbf{y} = \mathop{\mathrm{argmax}}_{\mathbf{y}\in \{\langle \mathbf{y}_i^{n-1},~y \rangle ~|~ i \in 1\dots |Y|~\wedge~ y \in Y\}} P(\mathbf{x}, \mathbf{y} ~|~ \Pi, A, B) $$

这就提出了以下算法：

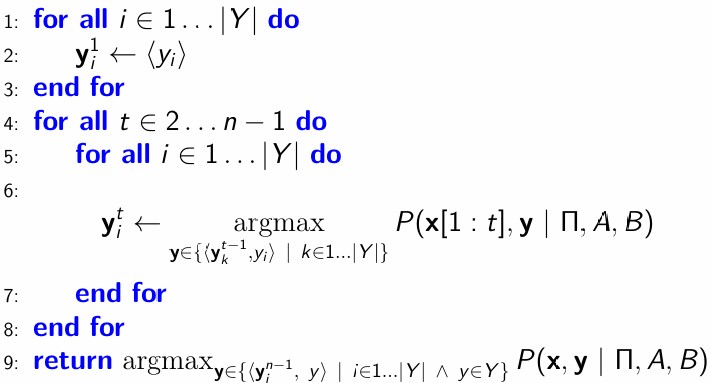
算法通常通过逐步填充一个 $|Y| \times \mathrm{length}(\mathbf{x})$ 表来实现。在前向传递中，它

1. 计算 $y_i^t$ 的概率，并
2. 维护到最可能的 $\mathbf{y}^{t-1}$ 的反向引用

在后向传递中，选择最可能的 $y_i^n$ 并通过跟随反向引用恢复 $\mathbf{y}$。

维特比是一种 动态规划 算法，与穷举搜索形成鲜明对比，其时间复杂度为 $\mathcal O(\mathrm{length}(\mathbf{x})|Y|^2)$

跟踪部分 $\mathbf{y}_i^t$ 序列元素及其概率的表仅占用 $\mathcal{O}(\mathrm{length}(\mathbf{x})|Y|)$ 空间。

直接计算要比较的概率需要乘以非常接近于零的数字，因此通常使用对数概率的和来进行计算。

注意：正如我们所见，维特比算法也被称为 最小和 或 最大积 算法的应用。

判别序列标注方法

Discriminative methods

与朴素贝叶斯序列分类器类似，HMM 是生成模型，建模输入和标签的概率，这在我们的设置中是不必要的。我们可以通过“反转”输入和标签之间的箭头并对 $\mathbf{X}$ 进行条件化来构建类似结构但判别的模型：

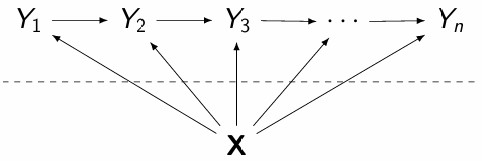
最大熵马尔可夫模型

Maximum entropy Markov models (MEMMs)

根据前面的图形模型假设，

$$ P(\mathbf{Y}~|~\mathbf{X}) = P(Y_1~|~ \mathbf{X})\prod_{m=2}^n P(Y_m|Y_{m-1}, \mathbf{X}) $$

MEMMs 通过使 $Y_m$ 仅在当前观测 $O_m$ 上条件依赖来形式化这个通用模型：

$$ P(\mathbf{Y}~|~\mathbf{X}) = P(Y_1~|~O_1)\prod_{m=2}^n P(Y_m|Y_{m-1},O_m) $$

那么 $Y_m$ 如何依赖于 $\mathbf{X}$ 呢？诀窍在于如何定义 $O_m$。

特征函数

$Y_{m-1},O_m$ 对被定义为 $\mathbf{f}(y_k,\mathbf{x}, m)$，其中 $f(\cdot)$ 是一个基于 $Y_{m-1}=y_k$ 和 $x$ 在 $m$ 处生成 feature vector 的函数。

在 NLP 中，我们仅在要标注元素周围的上下文窗口内对local features进行条件化。由语言学家设计的一些用于词性标注的示例特征：

• 上下文窗口中 $x_m$ 周围的元素，例如 $\langle x_{m-1}, x_{m}, x_{m+1} \rangle$

• 上下文窗口元素的后缀（固定长度）

• 上下文窗口元素的前缀（固定长度）

• 上下文窗口元素的大小写信息

• 前一个元素的词性标注 $y_k$

MEMMs

个别的 $P(Y_m|Y_{m-1},X_m)$ 概率类似于使用 softmax 函数的multinomial logistic regression进行建模：

$$ P(Y_m = y_i|Y_{m-1}=y_k,\mathbf{x})=\frac{\exp (\mathbf{w}_i \cdot \mathbf{f}(y_k, \mathbf{x}, m))}{\sum_{j=1}^{|Y|}\exp (\mathbf{w}_j \cdot \mathbf{f}(y_k, \mathbf{x}, m))} $$

其中每个 $\mathbf{w}_i$ 是 $y_i\in Y$ 标签的权重向量。

MEMM 这个名称来源于在 NLP 中，多项逻辑回归更常被称为maximum entropy。

标签偏置

尽管 MEMMs 比 HMMs 更灵活（例如，标签可以依赖于上下文的其他特征而不仅仅是前一个标签），但它们也有重要的局限性。

也许最重要的是标签概率是局部归一化的：$\sum_{y\in Y}P(y~|y_{m-1}, \mathbf{x}, m)=1$，无论模型对上下文有多“熟悉”，因此模型无法表达对给定上下文中的标签的一般低置信度。

这导致了所谓的Label bias问题：模型无法轻易从在低置信度情况下做出的过去标注错误中恢复。

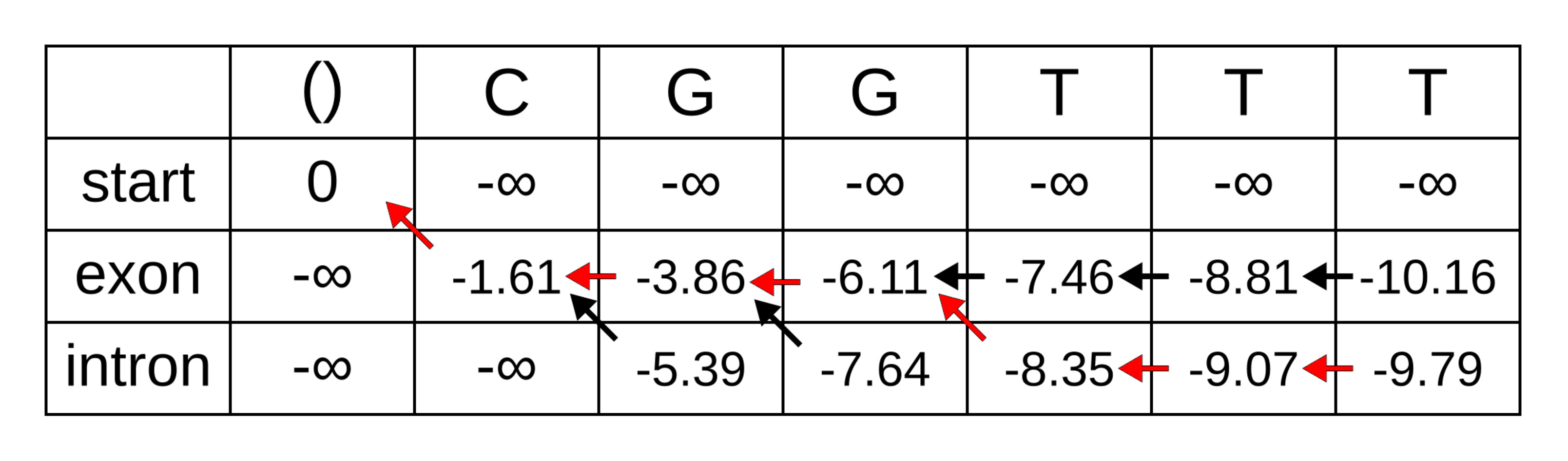
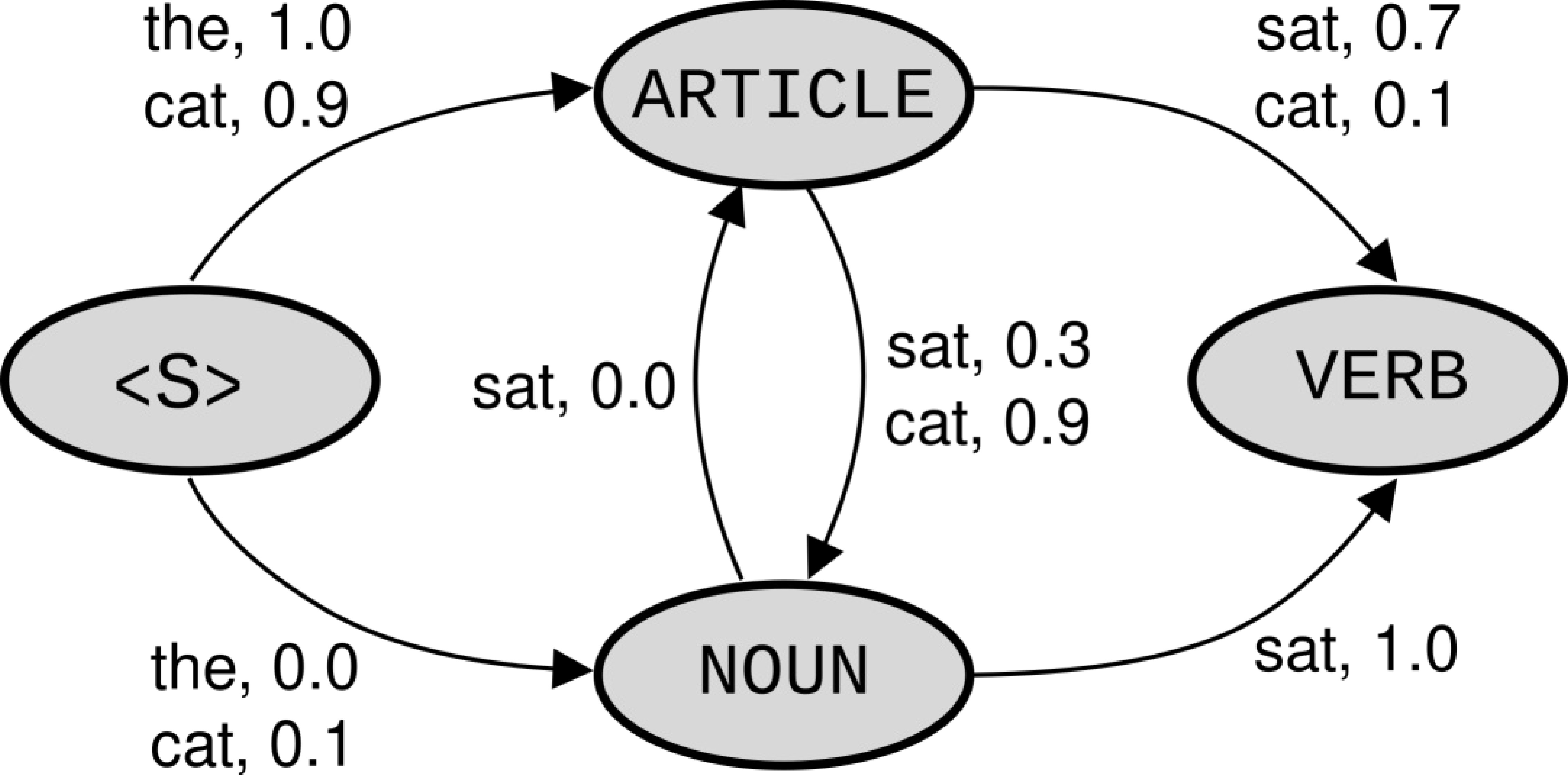
示例

一个词性标注器将句子 “cat sat” 标注为 ARTICLE VERB，因为

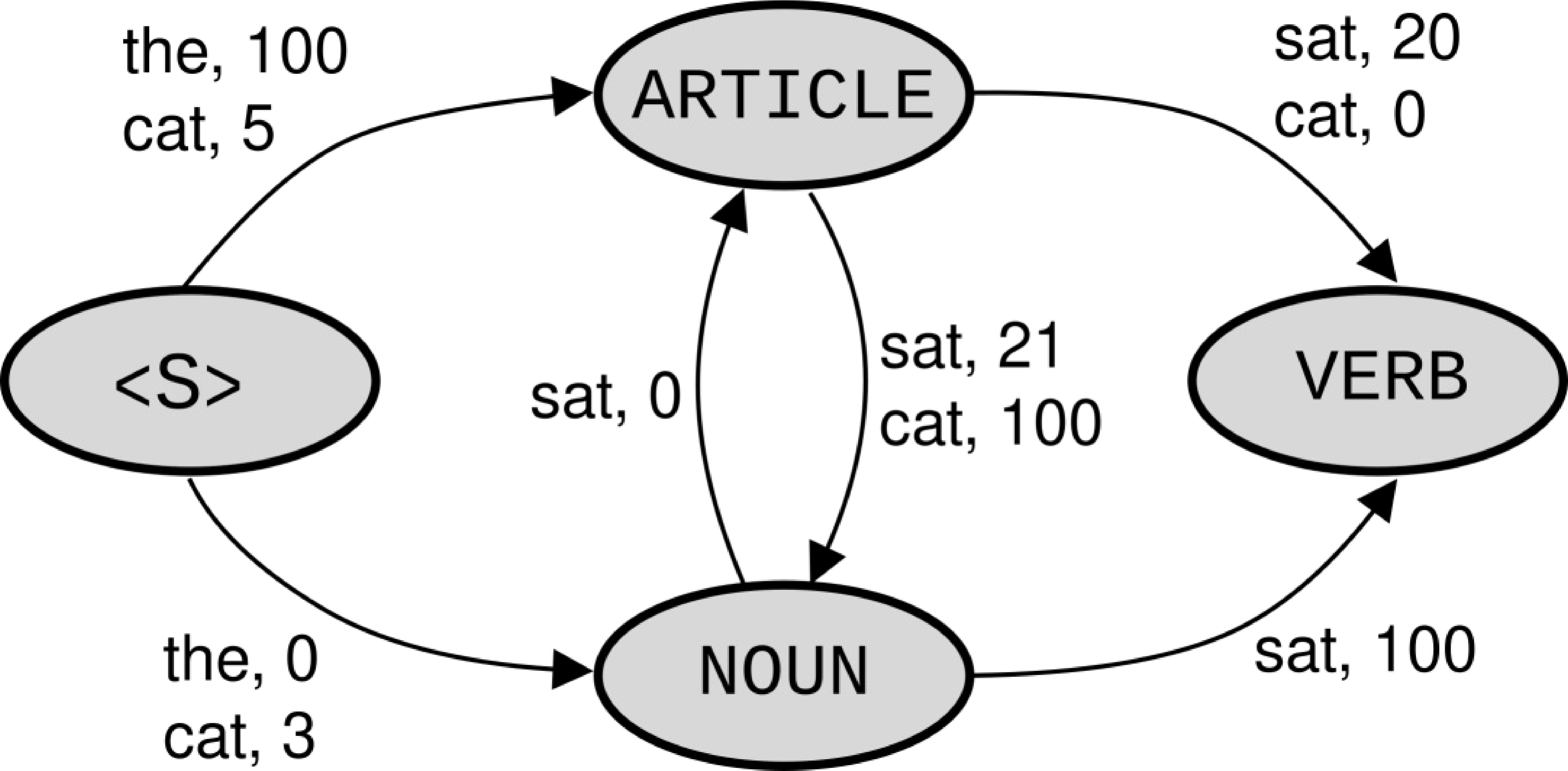
• 标注器无法从 <S> 处 cat 的偏斜后验分布（skewed posterior distribution）中恢复，使用局部归一化（图1）。

• 未归一化的 $\mathbf{w}_i \cdot \mathbf{f}(\cdot)$ 观测值（图2）显示

  1. 标注器对”cat“ 开始一个句子没有信心
  2. 全局 NOUN VERB 具有更高的分数（对数和沿边缘相加）

条件随机场

线性链条件随机场（Linear chain Conditional Random Fields）是判别模型，旨在避免标签偏置。它们假设以下 undirected 结构：

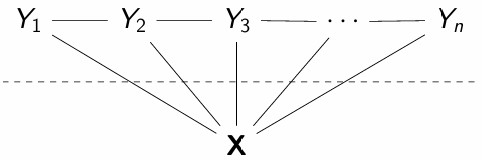
根据这些假设，

$$P(\mathbf{Y}~|~\mathbf{X}) = \frac{1}{Z(\mathbf{X})}\prod_{m=1}^{n-1} \phi_{m}(Y_m, Y_{m+1}, \mathbf{X})$$

与 MEMMs 有些类似，$\phi_m(\cdot)$ 势函数 （potential）通过特征函数和相应的权重向量线性建模。它们基本上是 softmax 的分子：

$$\phi_m(y_m, y_{m+1},\mathbf{x})={\exp (\mathbf{w} \cdot
\mathbf{f}(y_m,y_{m+1}, \mathbf{x}, m))}$$

关键区别在于归一化是全局的：

$$P(\mathbf{y}~|~\mathbf{x}) = \frac{\exp(\sum_{m=1}^{n-1}\mathbf{w}\cdot\mathbf{f}(y_m,y_{m+1}, \mathbf{x}, m))} {\sum_{\mathbf{y}'\in Y^n}\exp(\sum_{m=1}^{n-1}\mathbf{w}\cdot\mathbf{f}(y'_m,y'_{m+1}, \mathbf{x}, m))}$$

优化和推理

MEMMs 和线性链 CRFs 都可以使用标准的凸优化技术进行优化，例如梯度下降，并且在训练模型后，可以使用维特比算法的变体有效地找到给定输入的最可能标签序列。