RL-Midterm
希望我能顺利过关
大数定理
大数定律表述了什么?
大量 独立 且 相同 的 随机样本 的采样平均值会收敛到真实值。
马尔可夫属性
什么是马尔可夫性质?
下一个状态只跟当前状态有关,与之前的状态无关。
RL 元素
强化学习任务的主要元素是什么?绘制示意图来说明。
flowchart LR
subgraph s1[" "]
n4["策略"]
n1["代理"]
end
subgraph s2[" "]
n5["模型"]
n3["环境"]
end
n1 -- 行动 --> n3
n3 -- 奖励 / 新状态 --> n1
n4 --- n1
n3 --- n5
n1@{ shape: rounded}
n3@{ shape: rounded}
RL 类型
什么是:评估性反馈,指示性反馈,非关联任务,关联任务?
评估反馈,只使用获得的奖励来决定行动
指示反馈,使用外部信息来决定行动
非关联任务,只在一种情况下学习并采取行动
关联任务,在多种情况下学习并采取行动
网格世界
有如下的网格世界,有一个较近的出口回报为 1,另一个较远的出口回报为 10。底部是回报为 -10 的悬崖。网格世界是随机的,噪声为 0.5,奖励为 0,折扣因子 0.99。有两条路可选,对于一个 Q-Learning 代理,最优策略是什么,为什么?
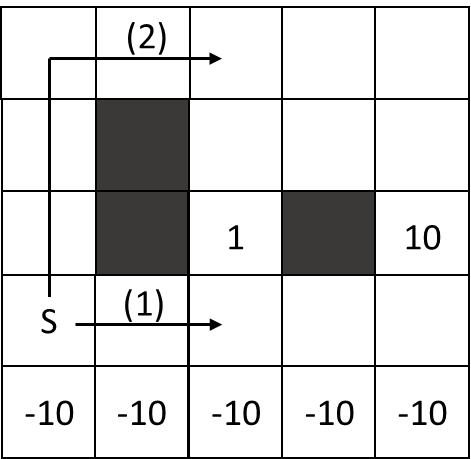
选择较远的出口,且避免悬崖。
- 高噪声可能导致行动不按期望执行,掉入悬崖。
- 高折扣因子导致未来,如终点,的回报很重要。
策略迭代
什么是广义策略迭代?
策略评估与策略改进交替进行的一种方法,不是某个特定算法,值迭代算法是一个实例。
困境
探索与利用的困境是什么?
很难平衡探索与利用的比率,无法同时追求两者
算法对比
比较 DP, MC, TD,每种方法的更新规则是什么?画出它们的备份图。
| DP | MC | TD |
|---|---|---|
| 需要环境模型 | 不需要环境模型 | 不需要环境模型 |
| 使用自举 | 不使用自举 | 使用自举 |
| 基于其他估值来更新 | 基于回合结束后的结果来更新 | 基于其他估值来更新 |
| 期望更新 | 样本更新 | 样本更新 |
| $V(S_t) \leftarrow E_{\pi} [R_{t+1} + \gamma V(S_{t+1})]$ | $V(S_t) \leftarrow V(S_t) + \alpha (G_t - V(S_t))$ | $V(S_t) \leftarrow V(S_t) + \alpha (R_{t+1} + \gamma V(S_{t+1}) - V(S_t))$ |
flowchart TD
subgraph s1[" "]
n2["Filled Circle"]
n3["Filled Circle"]
n1["Small Circle"]
n4["Small Circle"]
n5["Small Circle"]
n6["Small Circle"]
n7["Small Circle"]
end
n1 --> n2 & n3
n2 --> n4 & n5
n3 --> n6 & n7
n4 --> n8["Filled Circle"] & n9["Filled Circle"]
n5 --> n10["Filled Circle"] & n11["Filled Circle"]
n6 --> n12["Filled Circle"] & n13["Filled Circle"]
n7 --> n14["Filled Circle"] & n15["Filled Circle"]
n16["Small Circle"] --> n17["Filled Circle"]
n16 -- mark --> n18["Filled Circle"]
n17 --> n19["Small Circle"] & n20["Small Circle"]
n18 -- "mark" --> n21["Small Circle"]
n18 --> n22["Small Circle"]
n19 --> n23["Filled Circle"] & n24["Filled Circle"]
n20 --> n25["Filled Circle"] & n26["Filled Circle"]
n21 --> n27["Filled Circle"]
n21 -- "mark" --> n28["Filled Circle"]
n22 --> n29["Filled Circle"] & n30["Filled Circle"]
n28 -- "mark" --> n33["Frames Circle"]
n34["Small Circle"] --> n35["Filled Circle"]
n34 -- mark --> n36["Filled Circle"]
n35 --> n37["Small Circle"] & n38["Small Circle"]
n36 -- "mark" --> n39["Small Circle"]
n36 --> n40["Small Circle"]
n37 --> n41["Filled Circle"] & n42["Filled Circle"]
n38 --> n43["Filled Circle"] & n44["Filled Circle"]
n39 --> n45["Filled Circle"] & n46["Filled Circle"]
n40 --> n47["Filled Circle"] & n48["Filled Circle"]
n2@{ shape: f-circ}
n3@{ shape: f-circ}
n1@{ shape: sm-circ}
n4@{ shape: sm-circ}
n5@{ shape: sm-circ}
n6@{ shape: sm-circ}
n7@{ shape: sm-circ}
n8@{ shape: f-circ}
n9@{ shape: f-circ}
n10@{ shape: f-circ}
n11@{ shape: f-circ}
n12@{ shape: f-circ}
n13@{ shape: f-circ}
n14@{ shape: f-circ}
n15@{ shape: f-circ}
n16@{ shape: sm-circ}
n17@{ shape: f-circ}
n18@{ shape: f-circ}
n19@{ shape: sm-circ}
n20@{ shape: sm-circ}
n21@{ shape: sm-circ}
n22@{ shape: sm-circ}
n23@{ shape: f-circ}
n24@{ shape: f-circ}
n25@{ shape: f-circ}
n26@{ shape: f-circ}
n27@{ shape: f-circ}
n28@{ shape: f-circ}
n29@{ shape: f-circ}
n30@{ shape: f-circ}
n33@{ shape: fr-circ}
n34@{ shape: sm-circ}
n35@{ shape: f-circ}
n36@{ shape: f-circ}
n37@{ shape: sm-circ}
n38@{ shape: sm-circ}
n39@{ shape: sm-circ}
n40@{ shape: sm-circ}
n41@{ shape: f-circ}
n42@{ shape: f-circ}
n43@{ shape: f-circ}
n44@{ shape: f-circ}
n45@{ shape: f-circ}
n46@{ shape: f-circ}
n47@{ shape: f-circ}
n48@{ shape: f-circ}
E 贪婪
在有四个动作且 E=0.8 的 epsilon-greedy 策略中,如果已知只有一个贪婪动作,那么选中它的概率是多少?
- 0.2 选中贪婪动作
- 0.8 选中随机动作
其中 0.25 的概率选中贪婪动作
所以,选中贪婪动作的概率是 0.2 + 0.25 * 0.8 = 0.4
多情境
你面临一个 3 臂老虎机任务,其真实值随时间步随机变化,动作 1 2 3 的真实值如下:
| 情况 | 1 | 2 | 3 |
|---|---|---|---|
| A | 0.1 | 0.6 | 0.3 |
| B | 0.9 | 0.5 | 0.4 |
| C | 0.2 | 0.1 | 0.2 |
| D | 0.5 | 0.5 | 0.7 |
每种情况发生概率相同,问
- 如果你无法判断现在是哪种情况,你的最佳期望是多少,应如何行动?
- 如果你被告知当前的情况,但仍不知道真实值,你的最佳期望是多少,应如何行动?
如果我不知道当前情况,我只能根据经验选择动作,那么
- 动作 1 的期望值是 (0.1 + 0.9 + 0.2 + 0.5) / 4 = 0.425
- 动作 2 的期望值是 (0.6 + 0.5 + 0.1 + 0.5) / 4 = 0.425
- 动作 3 的期望值是 (0.3 + 0.4 + 0.2 + 0.7) / 4 = 0.4
所以,我应该选择动作 1 或 2,最佳期望是 0.425
如果我知道当前情况,我就可以选择最佳动作,那么
- 情况 A,我选择动作 2,0.6
- 情况 B,我选择动作 1,0.9
- 情况 C,我选择动作 1 或 3,0.2
- 情况 D,我选择动作 3,0.7
所以最佳期望为 (0.6 + 0.9 + 0.2 + 0.7) / 4 = 0.6
RL-Midterm