RL-规划与学习
Planing and Learning,Function Approximation都学了一半了才来理概念,怎么想的
RL 概念
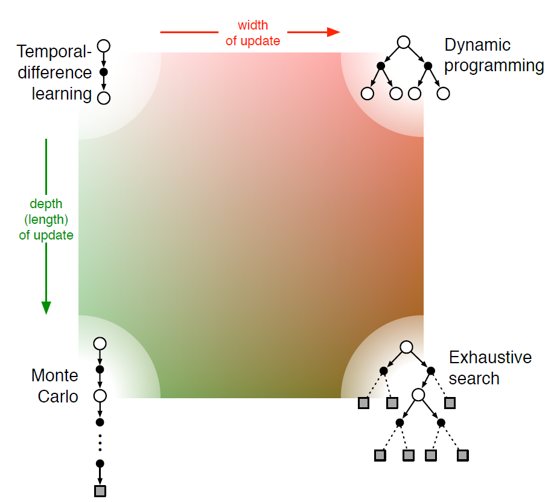
Tabular methods
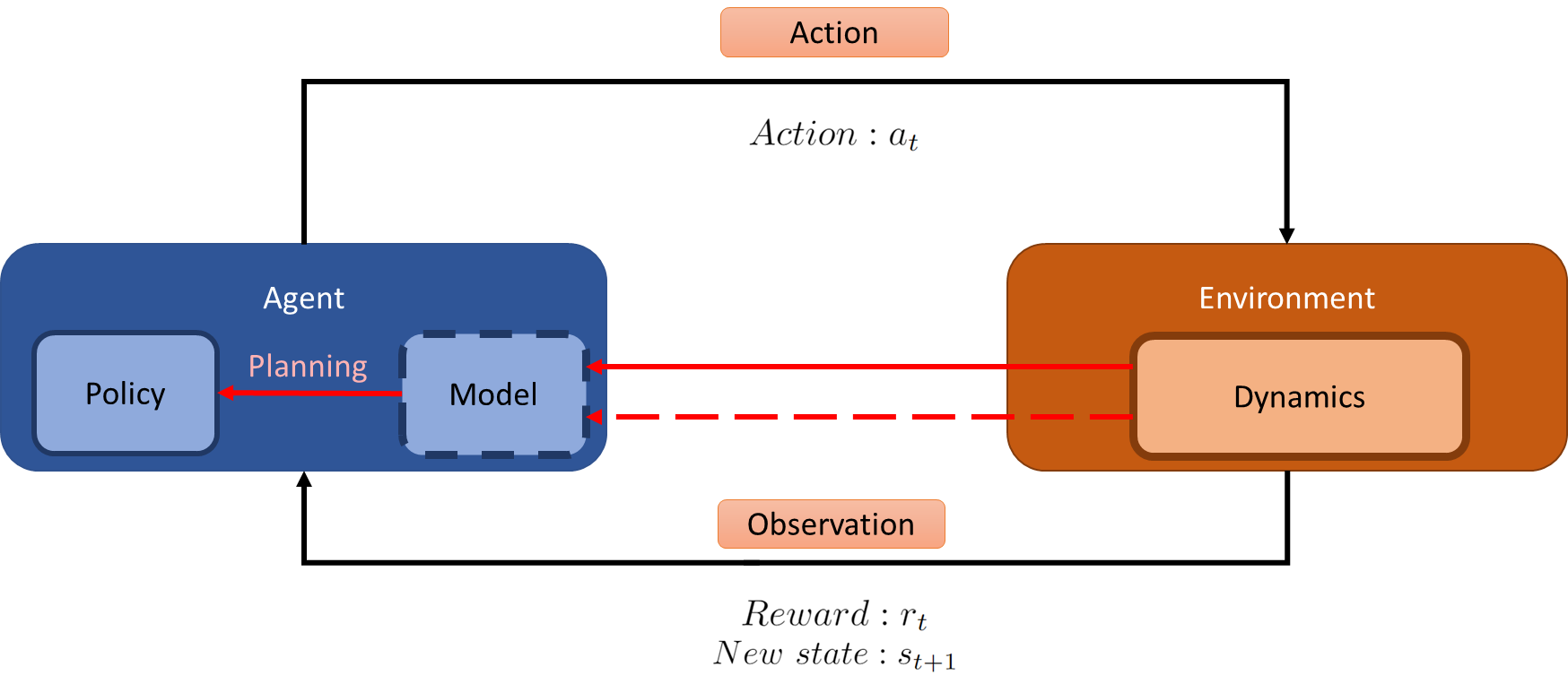
表格方法指的是基于有限状态和动作集合的方法,它们通常使用表格储存 State-Action Value Function。继续细分,可以分为 Model-Free (MC,TD,Learning) 和 Model-Based (DP,Heuristic,Planning) 方法。
Reflex / Planning
反射型代理的决策取决于当前感知(Perception),而规划型代理基于行动的后果。
反射型可以有环境模型,也可以没有,而规划型代理必须有环境模型。
反射型不考虑未来长期后果,适用于即时反应系统,而规划型代理会权衡短期和长期利益。
Model of the Environment
环境模型,是代理用来 预测环境如何响应其行动 的任何机制。可以是随机的,意味着一个动作可能导致多个不同状态。环境模型分为
- 分布模型(Distribution Model),生成所有可能的下一个状态和对应分布,适用于 DP 迭代。和
- 采样模型(Sample Model),只提供一个可能的下一个状态,按照真实概率进行采样,如 MC 方法。
Planning and Learning
规划的特点是基于模拟经验,使用环境模型生成的虚拟数据,不需要真实环境,适用于基于模型的方法。
学习的特点是基于真实经验,代理直接与环境交付,不需要环境模型,如 Sarsa。
规划和学习以可结合,如 Dyna-Q 方法。它们都是计算密集型任务,需要在规划和更新之间找到平衡。
Direct / Indirect RL
- 间接强化学习是基于模型的,真实经验用于改进模型环境,再用模型环境进行规划,代理就不需要与真实环境频繁交互,可以模拟更多数据。但是如果模型不准确,会导致错误的规划。
- 直接强化学习是基于真实经验的,不需要构建和维护环境模型,还没有偏差,但是数据效率低。
Dyna-Q
它结合了直接和间接强化学习,既从真实经验中学习,又从利用环境模型进行规划。
- 它首先采用 Q-Learning 从真实经验中学习,更新 Q 表格。
- 然后更新环境模型,将真实经验存储到模型中。
- 最后用模型进行规划,随机采样之前储存的经验,模拟训练 Q 表。
Dyna-Q = Q-learning + 经验回放(Planning)
此算法比 Q-Learning 更快,但是需要更多计算资源,适合与真实场景交互成本较高的情况。
我们还可以在模型中增加 时间衰减因子,让代理更倾向尝试那些长期未访问的状态,这就叫 Dyna-Q+,避免局部最优解。
函数近似
在 RL 中,我们可以使用函数近似来表示状态价值函数,而不是用表格来记录每个状态,即使遇到未知状态,也能估算出它的价值。是为了让强化学习能处理大规模或连续状态空间的问题,虽然它更强大,但也更复杂。
参数更少:函数的参数量远比状态总数少,在状态空间大的时候也能有效学习
泛化能力强:不需要为每个状态都单独学习
可处理部分可观测问题:不能完全看到状态也可以学习
难理解和调试:一个状态变化会影响很多其他状态
没有记忆能力:不能用过去的观测来增强当前状态的表示
而表格方法没有误差度量,因为每个状态都有单独的值,且各个状态互相独立。
所以,表格方法精确但不能泛化,函数逼近能泛化但可能不够精确。
损失函数
损失函数那肯定是用 MSE 了,然后就是之前讲过的梯度下降,不一样的是目标:
- MC 方法的目标是 $S_t \to G_t$,整个回合的奖励当目标
- TD(0) 方法的目标是 $S*t \to R_{t+1} + \gamma V(S_{t+1}, w_t)$,下一个状态的价值当目标
我们有随机梯度下降 SGD 和半梯度下降,SGD 使用少量随机选择的样本来更新参数以便加快速度,而半梯度在更新参数的时候只对估计函数求梯度,不对目标值求梯度,所以就不是完整的梯度。
半梯度并不严格的去最小化误差函数,所以不一定收敛到最优解,但是表现还行,并且更新简单快速,并且是在线学习的,使得它可以用于持续问题(无限回合)。
近似方法
我们可以使用简单的 状态聚合(State Aggregation)来逼近,简而言之,就是将多个相似状态合并(类似于卷积),如每四个状态合并为一个然后取平均。虽然不够精确(因为是阶梯形),但简化了问题并能进行有效学习,泛化能力强,适合大状态空间。
我们还可以使用线性函数逼近(Linear Function Approximation),这是一种特殊情况,它假设我们要学的值函数是权重向量 $\mathbf{w}$ 和 特征向量 $\mathbf{x}(s)$ 的线性组合。
$$
\hat{v}(s, \mathbf{w}) \doteq \mathbf{w}^\top \mathbf{x}(s) = \sum_{i=1}^{d} w_i \cdot x_i(s)
$$
- $\hat{v}(s, \mathbf{w})$:表示状态 $s$ 的估计价值(value estimate)。
- $\mathbf{w} = (w_1, w_2, …, w_d)$:权重向量,是我们要学的参数。
- $\mathbf{x}(s) = (x_1(s), x_2(s), …, x_d(s))$:状态 $s$ 的特征表示(feature vector)。
- 把这两个向量相乘(点积),就得到了当前状态的价值估计。
它计算简单、高效,梯度容易求,但是表达能力有限,无法表示复杂的非线性关系。在使用线性函数逼近时,梯度更新非常简单快速,直接用状态的特征乘以误差就能完成一次学习更新。
特征
特征(features)的设计很重要,把状态 $s$ 转换成特征向量 $\mathbf{x}(s)$ 这一步对学习效果有巨大影响。
- 如果你把状态“编码”得不好,那么再好的算法也学不好
- 把“领域知识”引入学习(如果“红灯”是重要信息,把“红灯是否亮”作为一个特征)
- 线性函数逼近的限制:不能表达特征之间的“相互作用”
如果 A 和 B 同时为 1 才重要,线性函数只能把它们分别处理,不能表示“两者共同出现的效果”。这就是为什么后来大家会用非线性方法(比如神经网络)来增强表达能力。
当状态空间复杂、函数形状难以用简单方法描述时,神经网络是最强大、通用的函数逼近工具。任何连续函数都可以被一个带有至少一层隐藏层、并且权重有限的神经网络逼近得任意精确。
Coarse
有一种特征构造方法叫 Coarse Coding(粗编码)
每个特征对应状态空间中的一个“圆形区域”。
想象一下你有一个二维地图,每个状态是地图上的一个点。
你可以在地图上画很多“圆”,每个圆代表一个特征。这些特征是二值的(0 或 1)
如果当前状态在某个圆里面,那这个圆代表的特征就是 1,否则就是 0。
所以一个状态可以落在多个圆里,激活多个特征,也可能不在任何圆里。
这是一种“粗略地编码状态位置”的方法。
它不会精确告诉你状态在哪,而是说“状态大概落在哪些区域里”,
通过多个重叠的圆,状态之间也可以共享特征,从而实现泛化。
特征宽度的选择是函数逼近中非常重要的超参数:
- 特征窄:表达能力强,适合样本多的情况;
- 特征宽:更稳健,适合样本少的情况。
Tile
还有一种叫 Tile Coding(瓦片编码),它的特征就像是一个个矩形堆叠,每个瓦片对应一个特征。
它是一种用于多维连续空间的“粗编码”方法。
是对“coarse coding” 的一种扩展,不只是处理一维状态,而是可以处理 多个连续变量(例如位置 + 速度)
这种方法既灵活又计算高效。
灵活:可以根据不同任务设计不同数量和形状的“瓦片”
高效:激活的是离散的、稀疏的特征,更新时速度很快非常适合用于表示序列数据(如时间步状态)
平移方式(offset)会影响模型如何“泛化”状态之间的关系。
均匀偏移 → 更规则、对称的泛化。
非对称偏移 → 更灵活、复杂的泛化。
RL-规划与学习