RL-时序差分
Temporal Difference
入门
时间差分学习结合了 DP 与 MC 的优点,它不需要等待回合结束,也不需要环境模型。$TD(0)$ 是最简单的 TD 学习方法,它的更新公式为
$$
V(S_t) \leftarrow V(S_t) + \alpha [R_{t+1} + \gamma V(S_{t+1}) - V(S_t)]
$$
其中:
- $V(S_t)$:当前状态的估值
- $R_{t+1}$:即时奖励
- $\alpha$:学习率
- $\gamma$:折扣因子
- $R_{t+1} + \gamma V(S_{t+1})$:TD 目标,对未来回报的估计
在过程中根据新信息动态调整预测的方式,是 TD 的核心思想,例如:你每天开车从学校回家,假设出发的时候预测需要 30 分钟,但是由于路上发现下雨,你调整预测为 40 分钟,但后来你发现路上没有什么车,所以调整为 35 分钟,但快到家的时候堵车了,最终花了 45 分钟到家。
我们可以使用 Batch Updating 的方式,计算 TD(0) 但不立即更新估值,而是等一批次结束后统一更新,这样可以减少噪声,提高稳定性。在有限 MDP 中,使用小学习率,TD(0) 可以保证收敛。相比于 MD,虽然也会收敛,但是 TD 与 MD 会收敛到不同的解,并且 TD 更快,解更好。
预测示例
在一个未知的马尔可夫奖励过程(去掉 action 的 MDP)中,我们观察到以下八个回合:
| Episode | 状态序列 |
|---|---|
| 1 | A → 0 → B → 0 |
| 2 | B → 1 |
| 3 | B → 1 |
| 4 | B → 1 |
| 5 | B → 0 |
| 6 | B → 1 |
| 7 | B → 1 |
| 8 | B → 1 |
根据数据,你认为最优的预测是什么?即 $V(A)$ 和 $V(B)$ 的最佳值是多少?
要解决这道题,首先要理解 0 和 1 代表奖励,如回合 2,B 状态的奖励是 1。
flowchart LR
n1(("A")) -- "r = 0, 100%" --> n2(("B"))
n2 -- "r = 0, 2/8 = 25%" --> n3["Filled Circle"]
n2 -- "r = 1, 6/8 = 75%" --> n4["Filled Circle"]
n3@{ shape: f-circ}
n4@{ shape: f-circ}
我们可以简单的统计然后画出上述的状态转移图,然后计算 $V(A)$ 和 $V(B)$ 的值:
如果使用 TD(0),则 B 终止时的奖励分布为:
$$
V(B) = 0.25 \times 0 + 0.75 \times 1 = \frac{3}{4}
$$
然后我们使用公式反推 $V(A)$:
$$
V(A) = R + \gamma V(B) = 0 + 1 \times \frac{3}{4} = \frac{3}{4}
$$
如果使用 MC,那么它是基于完整回合计算平均回报,则 $V(B) = 0.75$。在观察到的所有回合中,A 的奖励都是 0,所以 $V(A) = 0$。
Sarsa
TD 更适用于在线学习,Sarsa 在策略内部进行学习 (On-Policy),它的名字来源于它的更新方式:
$$
(S_t, A_t, R_{t+1}, S_{t+1}, A_{t+1})
$$
更新公式为:
$$
Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha [R_{t+1} + \gamma Q(S_{t+1}, A_{t+1}) - Q(S_t, A_t)]
$$
我们可以发现它与 T(0) 公式相似,只不过是从状态估值变成了动作估值。
有风网格世界
Windy Gridworld 是一个带有随机干扰的网格世界,用于研究 on-policy 算法。它在某些列存在风力,会让代理的垂直位置,根据风力大小发生变化。一般来说,我们需要训练代理在风的干扰下找到最短路径。此任务对于 MC 方法来说很困难,因为它需要完整的回合,而有风网格可能会让代理一直停留在某个位置,导致回合无法结束。而 TD 方法可以有效的学习。
Q-Learning
除了 On-Policy 的 Sarsa,还有 Off-Policy 的 Q-Learning,它的更新公式为:
$$
Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha [R_{t+1} + \gamma \max_a Q(S_{t+1}, a) - Q(S_t, A_t)]
$$
可以观察到它与 Sarsa 的区别在于,它使用了 $\max_a Q(S_{t+1}, a)$,即在下一个状态选择最大 Q 值的动作对应的值,而不是使用当前策略选择的动作。它始终关注在未来可能采取的最优动作,而不依赖于当前的行为策略。
它在特定条件下可以收敛到最优 Q 值:每个 State-Action 被充分探索,学习率随着时间推移逐步减少但不为零,折扣因子保证在有限步数内对未来奖励有足够的重视。
Cliff Walking
悬崖行走是一个经典任务,用来比较 Sarsa 和 Q-Learning 的性能。简而言之,它是一个带有悬崖区域的网格世界,悬崖会导致很大的惩罚。根据实验我们可以发现,Sarsa 在执行任务时,会受到当前行为策略的影响,比如在 $\epsilon$ 较大的情况下,它更容易走进悬崖区域,尽管可能经过了充分探索,它的路径可能更为保守,仍有可能陷入次优路径。而 Q-Learning 总是根据最大化 Q 学习,因此会避开悬崖并快速找到通往终点的路径,即使在早期选择了错误动作,也能通过最大化来纠正。
Expected Sarsa
我们还可以折中一下,使用期望 Sarsa,它是 On-Policy 的,但在更新 Q 值时,使用所有可能动作的加权期望。它的更新公式为:
$$
Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha [R_{t+1} + \gamma \sum_a \pi(a|S_{t+1}) Q(S_{t+1}, a) - Q(S_t, A_t)]
$$
我们可以看到,它将下一个状态的所有可能动作的 Q 值加权求和,而不是选择最大的 Q 值。它相比于 Q-Learning 更稳定,相比于 Sarsa 更高效。
Double Learning
我们需要先了解一个问题:在使用最大 Q 值来估计最优策略时,可能会导致 正向偏差(Positive Bias)问题,比如 Q-Learning 中,我们还可以称其为 最大化偏差(Maximization Bias),这是因为 Q 值是采样来的,存在随机误差,而最大化操作倾向选择估值最高的动作,即使它是高估的,最终导致 Q 的值高于真实值。
而解决此问题的方法是双学习法。我们将所有实验数据分成两个独立的数据集,分别用来 确定最优动作 和 估计该动作的值。由于参与估计 Q 值的数据,没有参与选择最优动作,它就不会被最大化的偏差影响,进而得到更准确的估计。换言之,杜绝了自己又当运动员又当裁判的情况。
在公式中,它体现为两个独立的 Q 值表 $Q_1$ 和 $Q_2$:
$$
Q_1(S_t, A_t) \leftarrow Q_1(S_t, A_t) + \alpha [R_{t+1} + \gamma Q_2(S_{t+1}, \arg \max_a Q_1(S_{t+1}, a)) - Q_1(S_t, A_t)]
$$
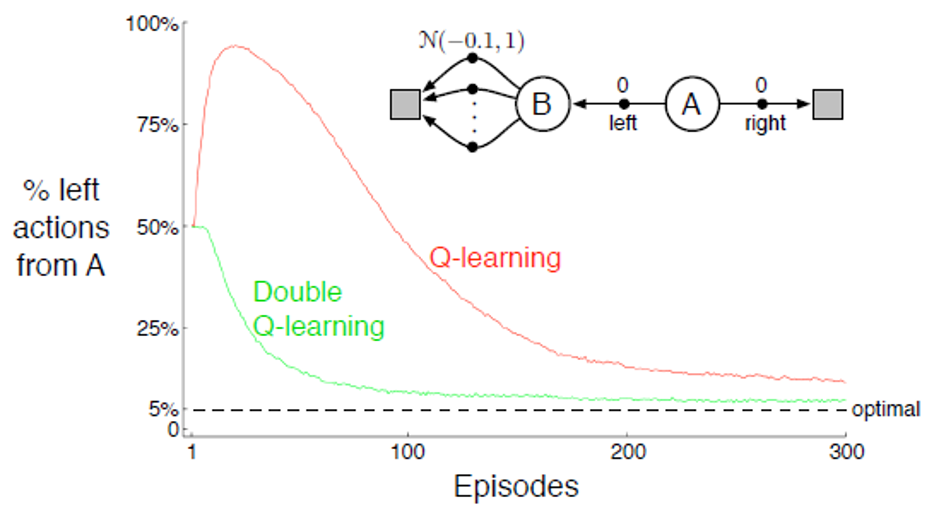
我们可以看到,绿色曲线更平滑,且收敛到更好的结果。虽然它不增加计算量,但是内存需求翻倍。
AfterState
后状态值函数(Afterstate Value Function)主要用于决策问题,如象棋围棋等。在普通状态价值函数中,我们评估的是整个状态,但并没有直接反应具体动作对状态的影响。而后状态函数将状态变为两个部分:初始状态(代理还没有做任何操作)和后状态(操作之后的变化),然后它评估的是行动后的新状态:
$$
V(s’) = E [\sum_{t=0}^{\infty} \gamma^t R_{t+1} | S_0 = s’, a_0 = a]
$$
例如,如果你需要在棋盘上选择一个最佳走法,传统方法要计算所有可能的动作后价值的加权平均,而 Afterstate 只需要计算走完一步后的状态价值,更加高效。
N 步自举
我们在 MC 和 TD(0) 中折中一下,MC 是等回合结束,TD(0) 是只需要一步。那么我们使用前 N 步奖励,再加上 N 步后的价值估计,即 N 步自举:
$$
G_t^{(N)} = r_t + \gamma r_{t+1} + \cdots + \gamma^{N-1} r_{t+N-1} + \gamma^N V(S_{t+N})
$$
N 越大,方法越接近蒙特卡洛方法,偏差减小但方差增大。N 越小,方法越接近 1-step TD,方差较小但可能会有较大的偏差。N-step 方法能够利用更长的回报信息,学习更加稳定。