RL-动态规划

Dynamic Programming
学不动了，真的

动态规划基础

我们都知道斐波那契数列计算

function fib(n: number): number {
  if (n === 0) return 0;
  if (n === 1) return 1;
  return fib(n - 1) + fib(n - 2);
}

这种朴素的递归算法，时间复杂度是指数级别的，$O(2^\frac{n}{2})$，我们可以用动态规划来优化。

const memo = [];

function fib(n: number): number {
  if (n === 0) return 0;
  if (n === 1) return 1;

  if (memo[n] !== undefined) return memo[n];

  memo[n] = fib(n - 1) + fib(n - 2);
  return memo[n];
}

它简单的将之前的计算结果保存下来，避免了重复计算，时间复杂度降到了$O(n)$。

这就引出了动态规划的两个重要概念：

DP = Recursion + Memoization

在强化学习中，动态规划是一组用来计算最优策略的算法集合。使用动态规划时需要给定环境的完美模型，我们使用 MDP 来描述此环境模型。就算使用动态规划，也需要消耗大量计算资源。

但是 DP 在处理大规模问题的时候仍然会遇到维度诅咒，并且需要确切的环境模型，才能进行评估和改进。

Policy Evaluation

前面我们讲到 State-value 函数用于评估某个状态的价值

$$
v_{\pi}(s) = E_{\pi}[R_{t+1} + \gamma v_{\pi}(S_{t+1}) | S_t = s]
$$

$$
= \sum_{a} \pi(a|s) \sum_{s’, r} p[s’, r|s, a](r + \gamma v_{\pi}(s’))
$$

由于此方程一般没有解析解，通常采用迭代的方式来求解，这就为我们后续进行策略改进提供了基础。

Grid World

我们在之前的 例：值迭代 中已经见过，这次让我们来看一道新的类型题目。

有一个已经计算好的策略如下：

x	1	2	3
4	5	6	7
8	9	10	11
12	13	14	x

0.0	-14	-20	-22
-14	-18	-20	-20
-20	-20	-18	-14
-22	-20	-14	0.0

奖励函数：-1，表示每一步都会受到 -1 的惩罚。

现在，让我们添加一个新的状态 15：

x	1	2	3
4	5	6	7
8	9	10	11
12	13	14	x
-	15	-	-

并且规定在 15 处执行：

• 左：15 -> 12
• 右：15 -> 14
• 上：15 -> 13
• 下：15 -> 15

问 1，设原状态转移的情况保持不变，在等概率随机策略的情况下，状态 15 的价值是多少？

问 2，现在假设从 13 执行向下会到 15，状态 15 的价值是多少？

问 1

要注意，原状态转移情况不变的意思是，在 13 处向下不会进入到新状态 15。

我们知道 $\pi(a|s) = 0.25$，$p(s’ | s, a) = 1$，$r = -1$，$\gamma = 1$。

所以：

$v_{\pi}(15) = \sum_{4} 0.25 \sum_{s’, r} 1 \times [-1 + 1 \times v_{\pi}(s’)] =$
$0.25 \times [-1 + -22] +$
$0.25 \times [-1 + -20] +$
$0.25 \times [-1 + -14] +$
$0.25 \times [-1 + v_{\pi}(15)] =$
$-15 + 0.25 \times v_{\pi}(15)$

将 $v_{\pi}(15)$ 移到左边，得到：

$0.75 \times v_{\pi}(15) = -15$

$v_{\pi}(15) = -20$

问 2

由于 15 的移动特性，导致它实际上是 13 的别名，所以不会导致 13 或 15 的价值发生变化。

让我们来计算验证一下：

$v_{\pi}(15) =$
$0.25 \times [-1 + -22] +$
$0.25 \times [-1 + v_{\pi}(13)] +$
$0.25 \times [-1 + -14] +$
$0.25 \times [-1 + v_{\pi}(15)] =$
$-10 + 0.25 \times v_{\pi}(13) + 0.25 \times v_{\pi}(15)$

$v_{\pi}(13) =$
$0.25 \times [-1 + -22] +$
$0.25 \times [-1 + -20] +$
$0.25 \times [-1 + -14] +$
$0.25 \times [-1 + v_{\pi}(15)] =$
$-15 + 0.25 \times v_{\pi}(15)$

联立求解：

$0.75v_{\pi}(15) = -10 + 0.25 \times (-15 + 0.25v_{\pi}(15))$

$v_{\pi}(15) = -20$

$v_{\pi}(13) = -15 + 0.25 \times (-20) = -15 - 5 = -20$

因此，状态13和状态15的价值都是-20。

Policy Improvement

如果在某个状态下，选择另一个不同的动作能够带来更高的状态价值，那么就可以更新策略。显然，如果一个策略选择的动作在所有可能的动作中有最高的状态价值，那么这个策略就是最优策略。一种常见的改进方法是贪心策略。

将策略改进和策略评估结合起来，就可以得到策略迭代算法。我们首先评估所有状态价值，然后更新策略，如此循环直到收敛。在有限的 MDP 中，Policy Iteration 算法总是能够收敛到最优策略。

策略改进算法可能导致震荡（Oscillation），即在两个策略之间来回切换，可以引入一个变化率参数，当策略改进的变化率小于某个阈值时停止。我们还需要通过截断评估（Truncated Evaluation）来加速收敛，即只评估一定次数的状态价值。

完整评估的意思是使用贝尔曼迭代方程反复更新，直到变化率小于某个阈值。而截断评估则是只更新一定次数就立刻开始策略改进。

Value Iteration 是一种更高效的策略迭代算法，它不需要完整评估，而是在每次迭代中只更新一次状态价值，然后立刻进行策略改进。这样可以减少计算量，但是可能会导致策略不稳定。

Asynchronous DP

我们还可以使用异步 DP，它不需要对所有状态进行同步更新，可以只更新部分状态的值。允许在不同时间更新不同状态，甚至可以有优先级，比如靠近目标的状态可能比远的更重要。异步更新不需要像同步 DP 那样储存当前轮和上一轮的值函数，因为它可以就地更新。

Generalized Policy Iteration

广义策略迭代并不是一个具体算法，它就是由上面的 Policy Iteration 和 Value Iteration 两种策略组合而成的。在每次迭代中，我们都会评估当前策略，然后改进策略。这样可以保证策略迭代算法收敛到最优策略。Value Iteration 就是一种应用。

Gambler’s Problem

一个赌徒有机会对一系列抛硬币的结果进行下注。如果硬币正面朝上，他赢得的金额与他在该次下注的金额相同。如果硬币反面朝上，他就会输掉所下堵住。当赌徒达到 100 收入则获胜，或者输光所有钱而失败。每次抛硬币时，他需要自己决定下注金额。

此问题可以被描述为一个 $\gamma = 1$ 的有限 MDP，状态是他的资金 $s \in {1, 2, …, 99}$，动作是他的下注金额 $a \in {0, 1, 2, …, \min(s, 100 - s)}$，奖励是 0，除了在 $s = 100$ 时奖励为 1。策略是从资金水平到下注金额的映射。$p_h$ 表示硬币正面朝上的概率，知道它即可求解。

你能猜出最优价值函数和最优策略是什么样的吗？

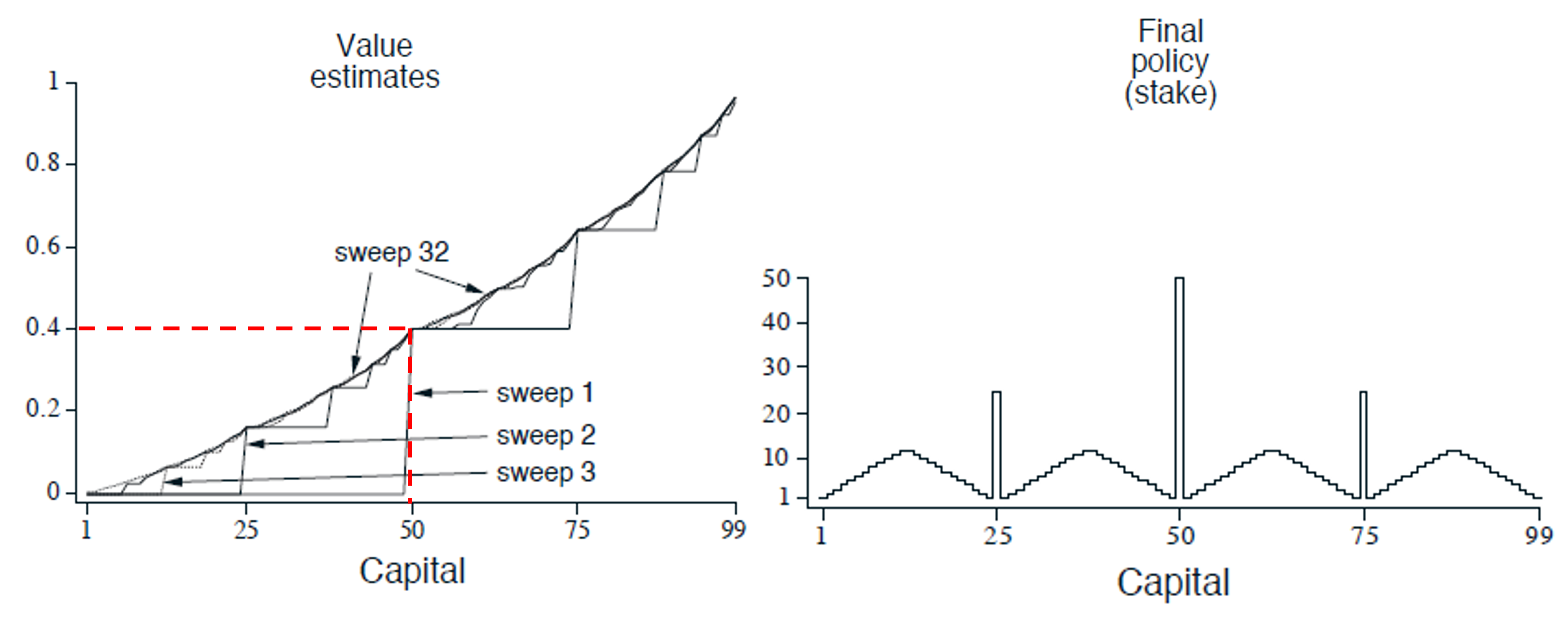
此问题使用 DP 的 Value Iteration 算法可以求解。

最优策略之所以具有这种奇怪的形式，特别是在资本为 50 时选择全押，而资本为 51 时却不全押，是因为最优策略不仅仅是考虑单次胜负，而是考虑达到目标（赢得 $100）的最优路径。在 50 时，全压可以直接赢得游戏，而在 51 时：

1. 51 视为 50 + 1，也就是说我们可以考虑如何利用额外的 1 元来赢得游戏。
2. 如果压 50，赢了就 101 了，但是 101 没有收益，没有意义。输了就回到 1，几乎等于输掉了游戏。赢的概率是 $p_h$。
3. 最好的办法是先压 1 美元，输了回到 50 再继续压。

Problem Buildup

如果模型已知，状态空间小且有限，动作空间小且有限的情况下，使用启发式搜索是很好的选择。

Search Trees 中的每个节点都对应着 State Space Graph 中的一条完整路径。

如果搜索空间很大，那么使用 DP 是更好的选择。如果模型未知，就需要使用 Monte Carlo 方法。