NLP-VisualModels

编码器-解码器式视觉语言模型

介绍

条件语言建模

任务是对条件分布进行建模

$$
P(\langle y_1,\dots,y_n\rangle|C)
$$

其中 $C$ 表示生成的 $\langle y_1,\dots,y_n\rangle$ 文本的一些条件，例如：

• 某种风格的文本
• 某个主题的文本
• 机器翻译
• 问答
• 从结构化数据生成自然语言（例如新闻）
• 图像描述

视觉条件

图像描述并不是唯一的条件语言建模任务，其中条件至少部分是视觉的，其他任务包括：

• 光学字符识别 (OCR)
• 视觉问答 (VQA)：回答关于图像的问题
• 自然语言视觉推理 (NLVR)：判断自然语言陈述在两张图像中是否为真
• 多模态翻译：基于上下文图像从一种语言翻译到另一种语言
• 多模态聊天：与混合图像和文本的用户输入进行聊天

编码器-解码器的解决方案

使用 编码器-解码器 架构来解决这些建模任务是一种自然的方法，其中

• 使用通常用于语言建模的 自回归文本解码器 生成文本（例如，LSTM 或 transformer 解码器）
• 解码器的文本输出通过接收来自 编码器 的适当编码形式的（部分）视觉输入来进行条件化

我们已经看到的一个经典示例是使用基于 CNN 的编码器和 LSTM 作为解码器的图像描述模型：

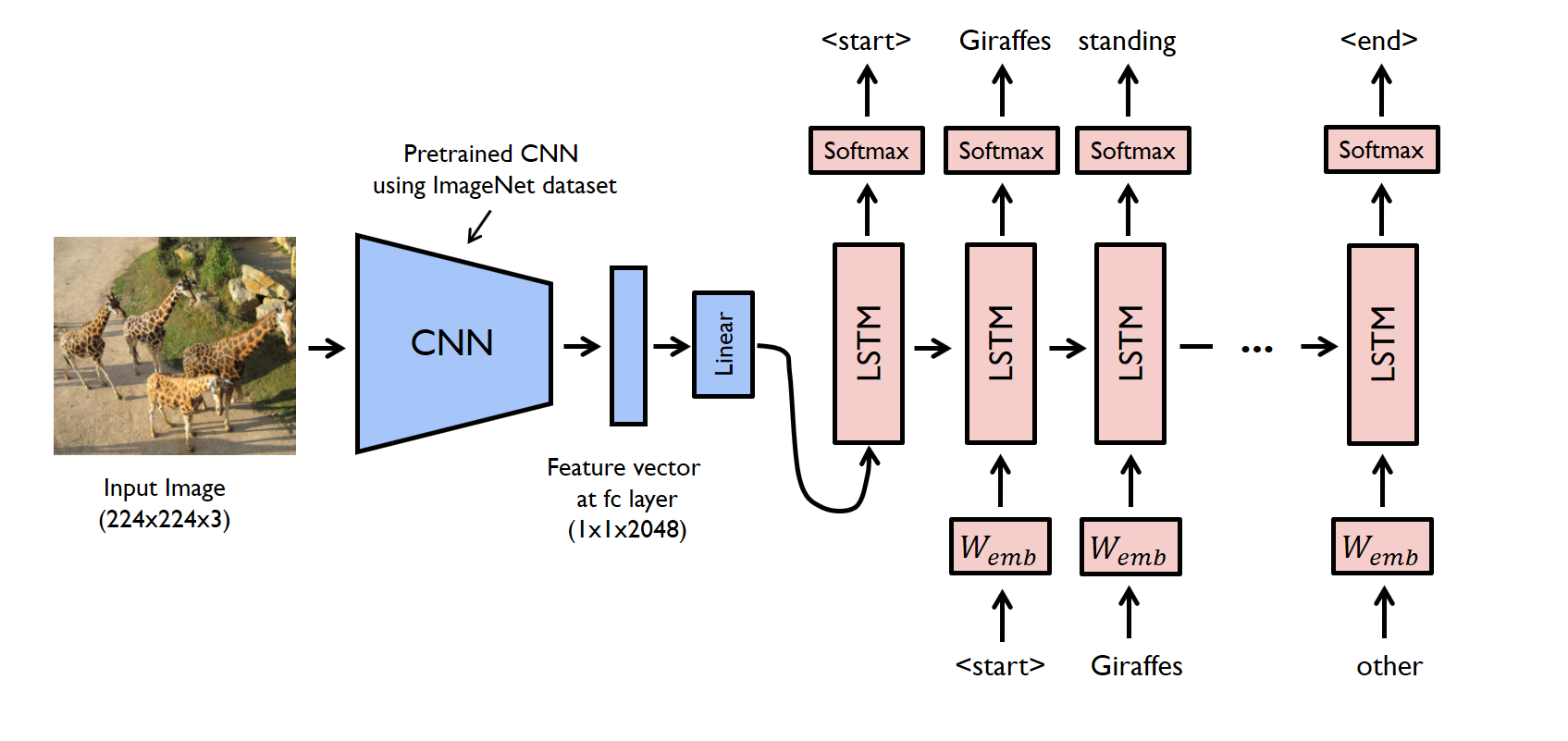
挑战

在基于 transformer 的预训练 LLMs 的最新进展背景下，将这种编码器-解码器方法应用于视觉条件文本生成的主要挑战是

• 编码图像，尤其是高分辨率图像，转换为适合 transformer 文本解码器的输入。由于标准输入是符号序列，这需要某种形式的 “视觉标记化”
• 扩展预训练的 LLM 解码器 以能够处理视觉输入：
  • 架构上：如何准确地连接编码器
  • 训练方面：如何利用 预训练 的编码器和解码器组件？

视觉标记化

符号表示

Transformers 设计用于处理符号序列。在视觉数据的情况下，这提出了一系列问题：

• 图像如何变成符号序列？
• 如何为这些符号分配有意义的嵌入向量？
• 需要什么样的位置编码？
• 多尺度处理怎么办？

视觉标记器

视觉标记化通常包含以下步骤：

• 分块（将图像拆分成较小的部分）
• 块嵌入（通过学习层、CNN 等）
• 位置编码（学习的、固定的、1D、2D 等）

最激进的视觉标记器不是使用 连续 变换将图像块嵌入到嵌入空间，而是将块映射到有限的 代码簿 中的嵌入，通常只包含几千个嵌入条目。

结果是编码的图像表示几乎完全类似于现代语言模型中使用的文本表示：

• 存在一个视觉 词汇表
• 在代码簿中有相关的 嵌入
• 图像表示为按顺序或网格排列的词汇元素（“视觉词”）

生成这些离散表示的一种突出方法依赖于 离散变分自编码器。

变分自编码器

变分方法

在概率建模中经常出现以下情况：

• 我们对复杂的 $p^{*}$ 分布的性质感兴趣，

• 但只能计算未归一化的 $\tilde{p}$ 函数的值，其中

$$ p^*(\mathbf x) = \frac{\tilde{p}(\mathbf x)}{Z} $$

$Z$ 是常数归一化因子（对于连续的 $p^*$，$Z = \int \tilde{p}(\mathbf x)d\mathbf x$），其计算是不可行的。

解决该问题的变分方法是用一个更简单、可处理的 $q$ 分布来近似复杂的 $p^*$ 目标分布，该 $q$ 分布由一些可调参数 $\Theta$ 参数化。

近似需要某种距离度量，KL 散度

$$ \mathbb{KL}(p^*\Vert q) = \mathbb E_{\mathbf x \sim p^*}\log\frac{p^*(\mathbf x)}{q(\mathbf x)} $$

是一个自然的选择，但计算这个也是有问题的，因为它需要对 $p^*$ 进行期望计算。

选择反向 KL 散度

$$ \mathbb{KL}(q\Vert p^*) = \mathbb E_{\mathbf x\sim q}\log\frac{q(\mathbf x)}{p^*(\mathbf x)} $$

将对假设可处理的 $q$ 进行期望计算，但仍然需要逐点评估 $p^*$，因此变分目标是最小化 $q$ 和未归一化的 $\tilde p$ 之间的“准 KL 散度”：我们试图找到

$$ \underset{\Theta}{\operatorname{argmin}} \left(\mathbb E_{\mathbf x \sim q_\Theta}\log\frac{q_\Theta(\mathbf x)}{\tilde p(\mathbf x)}\right) $$

就我们的目标 $p^*$ 而言，目标可以写成

$$ \mathbb E_ {\mathbf x \sim q_\Theta}\log\frac{q_\Theta(\mathbf x)}{p^*(\mathbf x)Z} = \mathbb{KL}(q_\Theta\Vert p^*)-\log Z $$

由于 Gibbs 不等式保证 $\mathbb{KL}(q_\Theta\Vert p^*)\geq 0$，所有值将是 $-\log Z$ 的上界，任务是找到最小的（所谓的变分）上界。

等效的最大化任务目标：

$$
\mathbb E_{\mathbf x\sim q_\Theta}\log\frac{p^*(\mathbf x)Z}{q_\Theta(\mathbf x)}d\mathbf x = \log Z - \mathbb{KL}(q_\Theta\Vert p^*)
$$

是找到 $\log Z$ 的最大（变分）下界。

应用

• 近似以下形式的 基于能量函数的分布

  $$ p(\mathbf x) = \frac{e^{-E(\mathbf x)}}{Z} $$

  其中 $E(\cdot)$ 是能量函数，上界 $- \log Z$ 被称为 自由能

• 变分贝叶斯：近似

  $$ p_\Theta(\mathbf z | \mathbf x) =\frac{p_\Theta(\mathbf x | \mathbf z) p_\Theta(\mathbf z )}{p_\Theta(\mathbf x)}$$

  生成模型的 $\mathbf z$ 潜变量的后验分布。在这种情况下，目标是找到 证据 $\log p_\Theta(\mathbf x)$ (ELBO) 的变分下界

变分自编码器 (VAE)

起点是包含潜变量的模型

• 潜变量 $\mathbf z$ 具有指数族分布，例如高斯分布

• 可观测变量 $\mathbf x | \mathbf z$ 具有分布 $p_\Theta(\mathbf x | \mathbf z ) = \pi_d (\mathbf x | d_\Theta(\mathbf z))$，其中 $d_\Theta(\cdot)$ 是一个解码器，例如 ANN，$\pi_d$ 是一个简单的分布，例如以 $d_\Theta(\mathbf z)$ 为中心的高斯分布

由于存在复杂的解码器，计算 $p(\mathbf z | \mathbf x)$ 后验或 $p(\mathbf x)$ 是不可行的，因此引入了一个辅助编码器来变分近似后验：

• 近似为 $q_\Phi(\mathbf z | \mathbf x)= \pi_e(\mathbf z | e_\Phi(\mathbf x))$，其中 $\pi_e$ 也是一个简单的分布，通常是均值和方差由 $e_\Phi(\cdot)$ 编码器输出的高斯分布

组合组件可以被认为是确定性自编码器的概率版本：

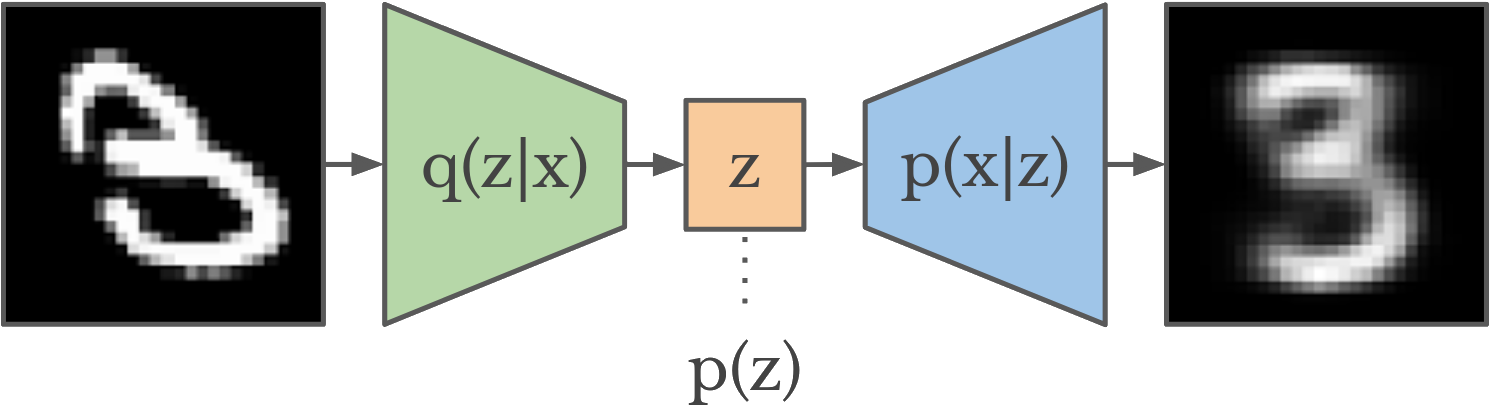
对于具体的 $\mathbf x$，用 $q_\Phi(\mathbf z | \mathbf x)$ 近似真实后验的变分目标是最小化

$$
\begin{align*}
\mathbb E_{\mathbf z \sim q_\Phi(\mathbf z | \mathbf x)}\log\frac{q_\Phi(\mathbf z | \mathbf x)}{p_\Theta(\mathbf x | \mathbf z)p(\mathbf z)} &= \
= \mathbb{KL}(q_\Phi(\mathbf z | \mathbf x)&\Vert p(\mathbf z))-\mathbb E_{\mathbf z \sim q_\Phi(\mathbf z | \mathbf x)}(\log p_\Theta(\mathbf x | \mathbf z))
\end{align*}
$$

在第二种形式中，

• $\mathbb{KL}(q_\Phi(\mathbf z | \mathbf x) \Vert p(\mathbf z))$ 相似性 可以以封闭形式计算
• $-\mathbb E_{\mathbf z \sim q_\Phi(\mathbf z | \mathbf x)}(\log p_\Theta(\mathbf x | \mathbf z))$ 可以解释为期望的 重构误差

重构误差

VAE 损失的

$$-\mathbb E_{\mathbf z \sim q_\Phi(\mathbf z | \mathbf x)}\log p_\Theta(\mathbf x | \mathbf z)$$

部分的重构误差解释需要将

$$- \log p_\Theta(\mathbf x | \mathbf z) = -\log \pi_d(\mathbf x | d_\Theta(\mathbf z))$$

重写为 $\mathbf x$ 和 $p_\Theta(\mathbf x | \mathbf z)$ 分布模式之间的某种距离，但在大多数情况下，这可以很容易地完成。

例如，如果 $\pi_d$ 是一个标准的球形 $m$ 维高斯分布，均值为 $d_\Theta(\mathbf z)$，则

$$ p_\Theta(\mathbf x | \mathbf z)= (2\pi)^{-m/2}\exp(-\Vert d_\Theta(\mathbf z) - \mathbf x\Vert^2/2) $$

因此，$$ - \log p_\Theta(\mathbf x | \mathbf z)= \Vert d_\Theta(\mathbf z) - \mathbf x\Vert^2/2 - \log ((2\pi)^{-m/2}), $$ 即负对数概率是 $\mathbf x$ 和分布均值 $d_e(\mathbf z)$ 之间平方欧几里得距离的移位和缩放版本，可以看作是“重构的 $\mathbf x$”，即 $\mathbf{\hat{x}}$。

VAE

因此，使用高斯分布的 $\pi_e$、$\pi_d$ 和 $p(\mathbf z)$ 我们有

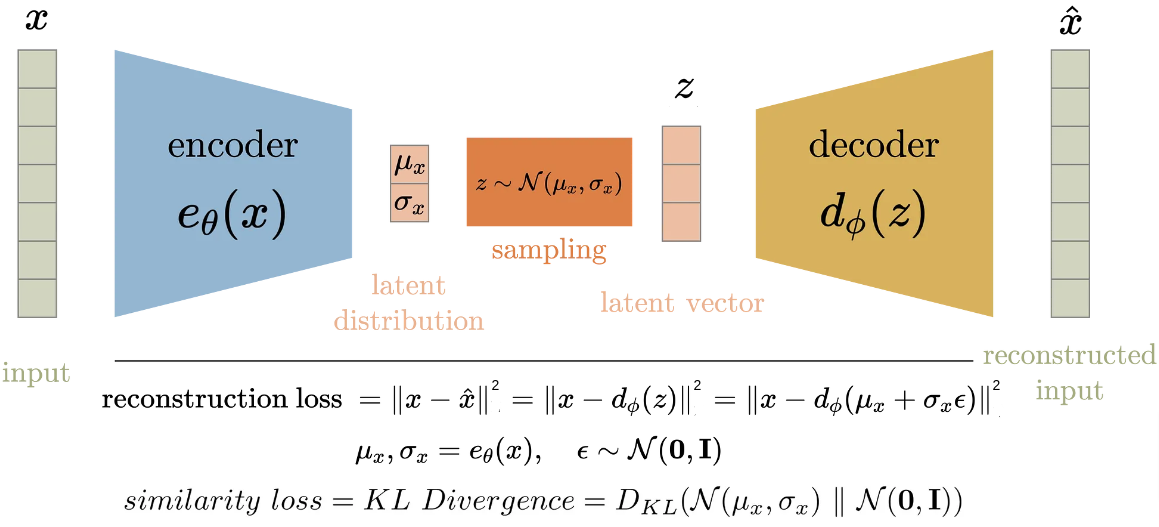
讨论的变分目标最小化与最大化训练集数据点的 $p_\Theta(\mathbf x)$ 的通常 MLE 目标有何关系？如我们所见，目标

$$
\underset{\Theta, \Phi}{\operatorname{argmin}}\left(\mathbb E_{\mathbf z \sim q_\Phi(\mathbf z | \mathbf x)}\log\frac{q_\Phi(\mathbf z | \mathbf x)}{p_\Theta(\mathbf x | \mathbf z)p(\mathbf z)}\right)
$$

也可以重写为

$$
\underset{\Theta, \Phi}{\operatorname{argmax}}\left( \log p_\Theta(\mathbf x)- \mathbb{KL}(q_\Phi(\mathbf z | \mathbf x) \Vert p_\Theta(\mathbf z | \mathbf x))\right)
$$

因此，找到最小化 $\Theta$ 和 $\Phi$ 实际上等同于找到对数似然的最大变分下界，即我们有一个 MLE 优化的变分近似。

重参数化技巧

VAE 通常使用梯度下降进行优化，但重构损失 $-\mathbb E_{\mathbf z \sim q_\Phi(\mathbf z | \mathbf x)}(\log p_\Theta(\mathbf x | \mathbf z))$ 涉及从 $q_\Phi(\mathbf z | \mathbf x)$ 采样，这使其不可微。

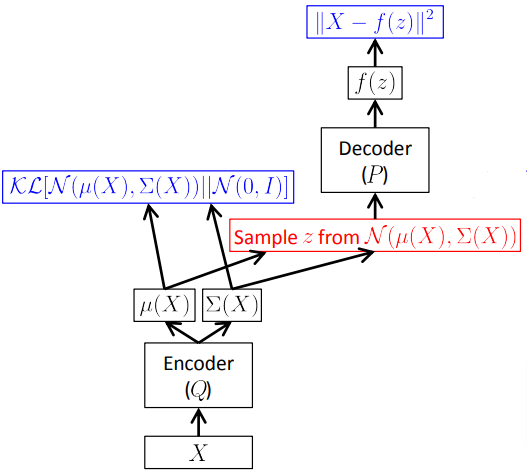
“重参数化技巧”通过将采样操作分解为从标准分布采样（与参数无关）和样本的依赖变换来解决这个问题。

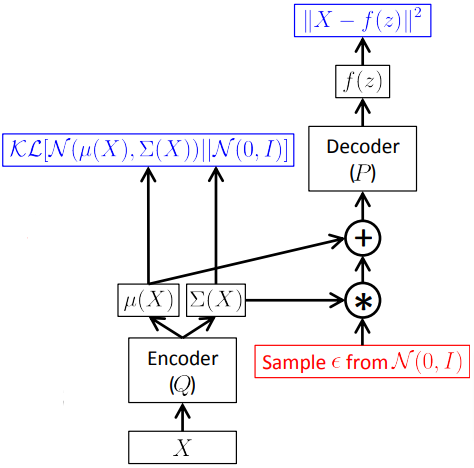
通过从常量分布 $q_0$（例如标准正态分布）采样和基于编码器输出的 $t$ 变换进行重参数化，我们可以将梯度运算符推入期望值内部：

$$
\nabla_{\Phi, \Theta}-\mathbb E_{\mathbf z \sim q_\Phi(\mathbf z | \mathbf x)}\log p_\Theta(\mathbf x | \mathbf z)
$$

可以重写为

$$
-\mathbb E_{\epsilon \sim q_0}\nabla_{\Phi, \Theta} \log p_\Theta(\mathbf x | t(e_\Phi(\mathbf x), \epsilon))
$$

并使用蒙特卡罗方法近似为

$$
-\frac{1}{n}\sum_{i=1}^{n}\nabla_{\Phi, \Theta} \log p_\Theta(\mathbf x | t(e_\Phi(\mathbf x), \epsilon_i))
$$

确定性 vs 变分自编码器

与确定性自编码器相比，VAE 是具有明确定义分布的真正生成模型。一个结果是，它们可以通过对潜在先验进行采样并解码它来生成高质量的新样本：

$\beta$-VAE

图像 VAE 使用标准 VAE 损失容易产生模糊图像，因为损失激励优化的解码器输出 $\mathbf{\hat{x}}=d_\Theta(\mathbf z)$ 重构，这是解码器映射到 $\mathbf z$ 的所有输入的平均值。

减少此问题的一种简单方法是减少相似性损失的权重，使自动编码器更接近确定性编码器：

$$\mathcal L_{\beta-VAE} = \beta\mathbb{KL}(q_\Phi(\mathbf z | \mathbf x) \Vert p(\mathbf z))-\mathbb E_{\mathbf z \sim q_\Phi(\mathbf z | \mathbf x)}(\log p_\Theta(\mathbf x | \mathbf z))$$

当 $\beta< 1$ 时，重构损失的权重大于正常 VAE 损失，而 $\beta=0$ 则导致完全确定性的自动编码器。

离散 VAE

到目前为止，我们假设潜在变量 $p(\mathbf z)$ 是连续的，但该架构也可以与 离散潜在变量 一起使用。

与连续情况相比，这需要

• 编码器中的 离散化层，将输入映射到离散代码
• 一种 训练方法，与 $p_\Theta(\mathbf z)$ 和 $q_\Phi(\mathbf z | \mathbf x)$ 为离散变量兼容

离散化

离散化编码器输出的策略包括

• 简单地将输入坐标 逐个舍入 到最近的整数代码，例如，当潜在变量被假定为二进制向量时，舍入到 0 或 1

• 完整的 向量量化：如果潜在变量是具有 $K$ 个离散值的分类集合（例如向量或矩阵），则来自 $\mathbb R^D$ 的输入向量可以使用学习的 代码簿 ${\mathbf e_k\in \mathbb R^D}_{k\in[1\dots K]}$ 映射到分类值。每个 $\mathbf e_i$ 输入嵌入被映射到最近代码簿条目的索引作为其潜在表示 $z_i$：
  $$
  z_i = \underset{k}{\operatorname{argmin}}(\Vert \mathbf e_i - \mathbf e_k\Vert_2)
  $$

VQ-VAE 离散化

在 VQ-VAE 方法中，$q(\mathbf z| \mathbf x)$ 潜在代码在第一个解码步骤中映射回相应的代码簿条目 $\mathbf e_{z_i}$：

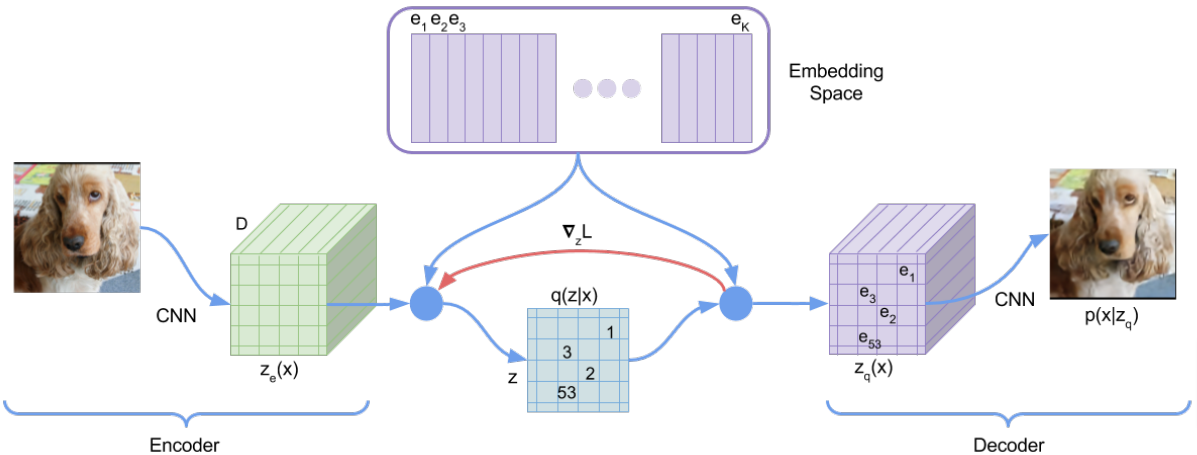
VQ-VAE 分布和损失

由于 VQ-VAE 解码器是确定性的且先验是均匀的，因此 $\mathbb {KL}(q(\mathbf z| \mathbf x)\Vert p(\mathbf z))$ 相似性损失是常数，可以忽略。量化是不可微的，因此只能使用所谓的 直通估计器，其中梯度从解码器传递通过量化层，就像它是恒等函数一样：

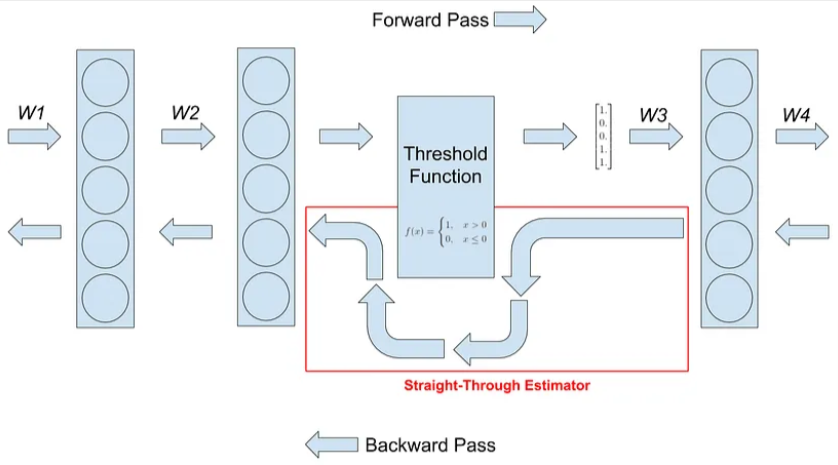
使用直通学习代码簿

基于直通方法的一个后果是代码簿没有梯度。学习代码簿的解决方案包括

• 引入一个额外的 代码簿损失 项，测量编码器输出和最近代码簿条目之间的距离。总损失变为
  $$
  \mathcal L=-\log p_\Theta (\mathbf x | \mathbf z_q(\mathbf x)) + \Vert sg(\mathbf z_{\mathbf e}(\mathbf x)) - \mathbf e\Vert_2^2
  $$
  其中 $sg$ 是 stop_gradient 操作符

• 定期更新代码簿条目，使其更接近分配给它们的输入的 移动平均值

使用 Gumbel-softmax 的离散 VAE

一种更有原则的方法来训练离散的、基于代码簿的、但真正概率的 VAE 使用一种适用于分类潜在变量的重参数化技巧版本。

该方法基于这样一个事实，即类似于从任何高斯分布采样，从任何分类分布采样也可以分解为从常量分布采样，然后确定性地变换样本。

所讨论的分布是具有密度函数的 标准 Gumbel 分布

$$
\mathcal G(x) = e^{-(x+e^{-x})}
$$

使用 Gumbel-softmax 的离散 VAE 续

$\mathcal G$ 标准 Gumbel 分布的一个重要性质是，如果分类分布由对数几率（logits）描述

$$
a_1, \dots, a_n
$$

那么可以通过从 $\mathcal G$ 中抽取 $n$ 个样本来对其进行采样：

$$
g_1, \dots, g_n\sim\mathcal G
$$

然后计算

$$
\underset{i}{\operatorname{argmax}} (a_i + g_i)
$$

样本变换中的 argmax 的存在使其不可微，但这可以通过以下方式解决

• 用 softmax 操作符替换它

• 让 $\mathbf z$ 潜在变量具有描述分类分布的任何向量作为值，而不仅仅是 one-hots

• 并将代码簿条目的 $\mathbf z$ 加权和传递给解码器

例如，对于输出单个分类潜在变量的对数几率的 $e_\Phi$ 编码器，这种 Gumbel-softmax 重参数化 产生的重构损失为

$$
\mathcal L_{rec}= - \mathbb E_{g_1,\dots,g_n \sim \mathcal G}
\log p_\Theta(\mathbf x | softmax_\tau(e_\Phi(\mathbf x)+ \langle g_1,\dots,g_n\rangle))
$$

并且可以通过通常的蒙特卡罗方法估计梯度。

softmax 对 argmax 近似的紧密性取决于 $\tau$ 温度参数：

$$
softmax_\tau(\langle x_1,\dots,x_n\rangle)= \left\langle\frac{e^{ x_1/\tau}}{\sum_{i=1}^n e^{ x_i/ \tau}},\dots, \frac{e^{x_n/\tau}}{\sum_{i=1}^n e^{x_n / \tau}}\right\rangle
$$

因此在训练期间逐渐降低 $\tau$，直到它接近 0。

DALL-E 视觉标记器

基于离散 VAE 的视觉标记器的一个重要示例是 DALL-E 中使用的标记器：

• 输入图像为 256x256
• 编码器和解码器都是卷积的
• 潜在变量 $\mathbf z$ 是一个 32x32 的分类变量网格，具有 8192 元素的“视觉词汇表”的均匀先验
• 解码器使用一种特殊的“logit-Laplace”分布，而不是通常的高斯和拉普拉斯分布（分别对应于 $L_2$ 和 $L_1$ 重构误差度量）
• KL 相似性损失的权重为 $\beta=6.6$，这导致了更好的代码簿使用，并在训练结束时导致更好的重构误差
• $\tau$ softmax 温度从 1 开始，在训练期间逐渐降低到 1/16

视觉 Transformer (ViT)

通用 ViT 架构

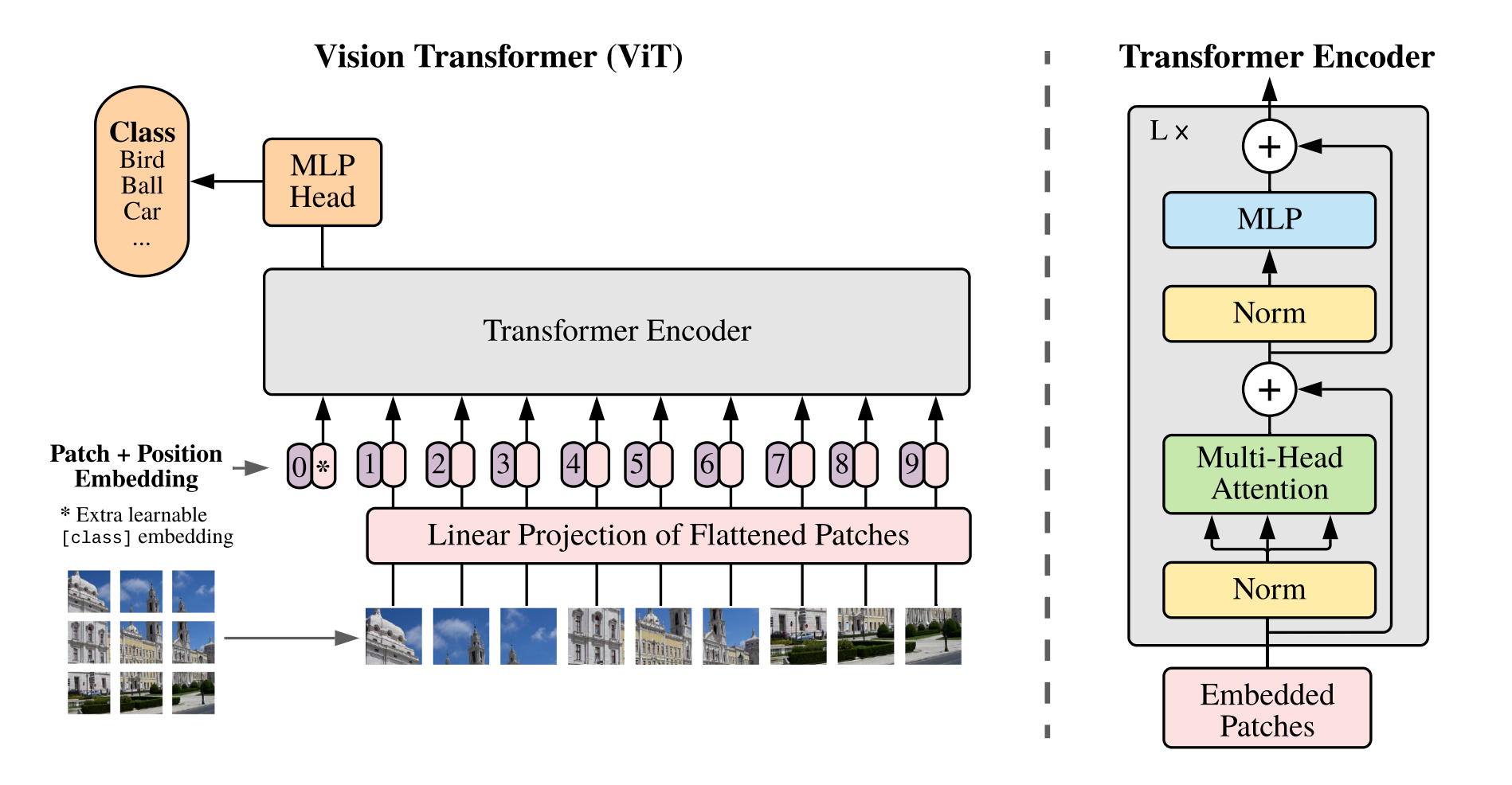
ViT 嵌入

通过使用特定的补丁大小 $P$ 对图像进行分块来创建嵌入。也可以使用步幅，$1\times1$ 的补丁也适用于逐像素处理。

每个补丁然后被输入到以下任一层：

• 展平后的线性投影层（学习的）
• CNN 主干（通常是固定的）

实验表明，对于普通的 ViT，1D 绝对位置编码效果最好。

ViT 分类标记

虽然补丁嵌入适用于局部图像表示，但分类还需要全局表示。
这是通过一个特殊的标记称为分类标记的可学习池化过程来实现的。

这个 CLS（或“类”）标记被预先添加到补丁嵌入中。该标记的初始值在训练期间被学习。

对应于该标记的输出用于分类。在预训练期间，这被输入到一个 3 层 MLP，而在微调期间使用单个线性层。

更高分辨率处理

由于较大的图像将被分解为较长的补丁序列，因此我们应该检查模型是否能够处理这一点。

MHA 和 FFN 仅包含逐点层，因此它们能够处理较长的序列。（由于 $W_Q, W_K, W_V$ 矩阵未针对这一点进行训练，可能会出现性能下降。）

唯一的限制因素是学习的位置编码。为了扩展这一点，可以使用简单的线性方法插值较长序列的位置编码值，以保持信息完整。

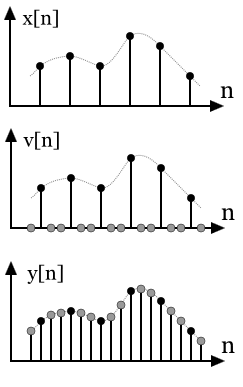
多尺度处理

SWIN - 分层 Transformer

SWIN 是一种基于 Shifted Window 的 Transformer 架构，能够使用多种分辨率级别处理任意大小的图像。
这种方法基于局部注意力的思想，其中注意力仅限于输入的某个特定区域。这是通过非重叠注意力窗口的窗口机制实现的。

在每个层次级别，标记通过可学习的投影进行合并（池化）（其他方法，如 T2T，将这些向量连接起来）。合并因子通常小于注意力窗口大小（例如：2x2 池化，4x4 注意力窗口）。

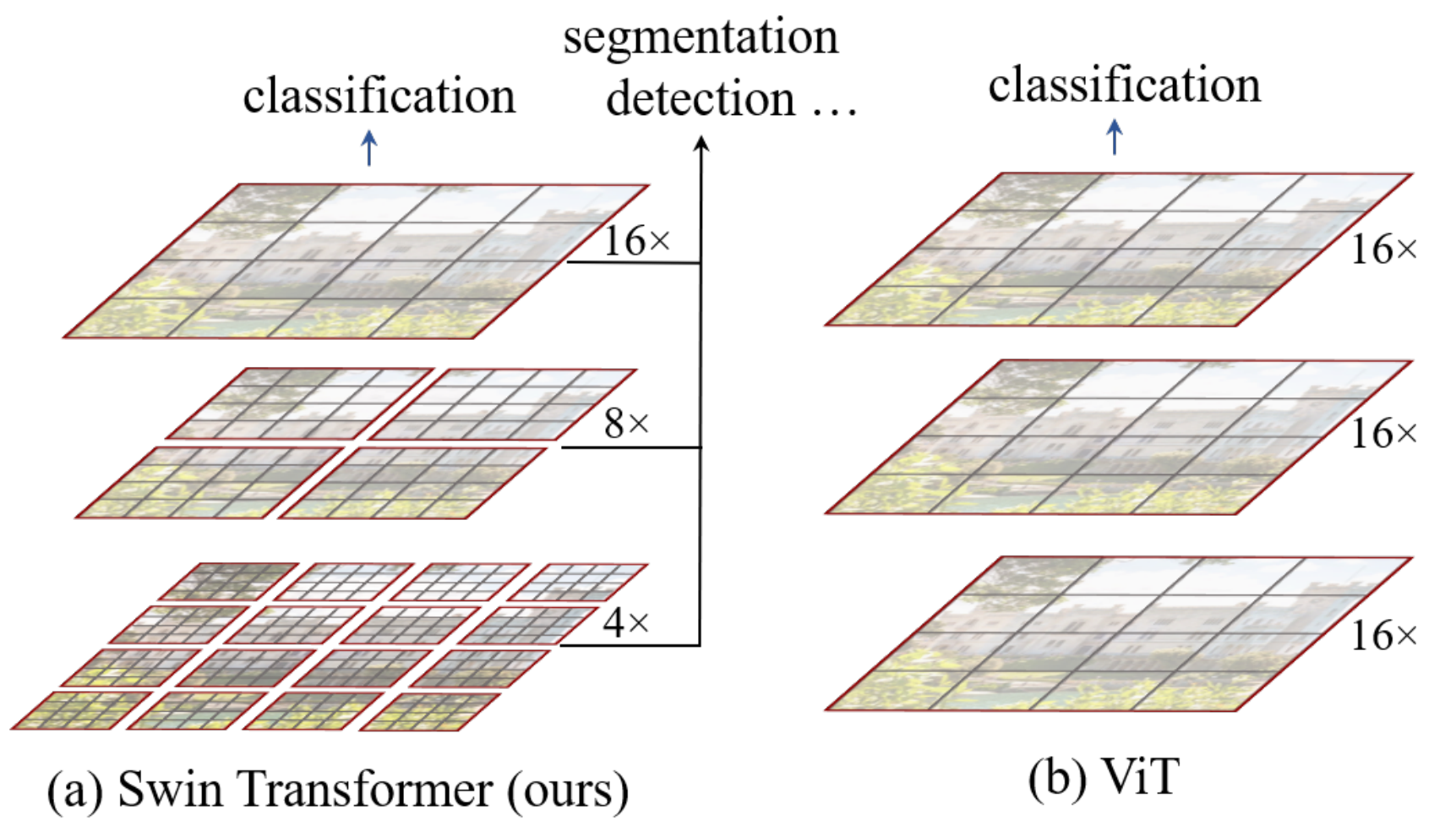
SWIN - 基于窗口的 MHA

通过使用这种窗口化注意力机制，MHA 的计算复杂度从二次降低到线性，其中 $h$ 和 $w$ 是补丁中 $C$ 通道图像的高度和宽度。

为了给出计算复杂度的下限，我们可以假设：

$\Omega(MHA) = 4\cdot hw \cdot C^2 + 2\cdot(hw)^2\cdot C$

$\Omega(MHA_{Windowed}) = 4\cdot hw \cdot C^2 + 2\cdot M^2 hwC$

假设 $M$ 是注意力窗口大小。

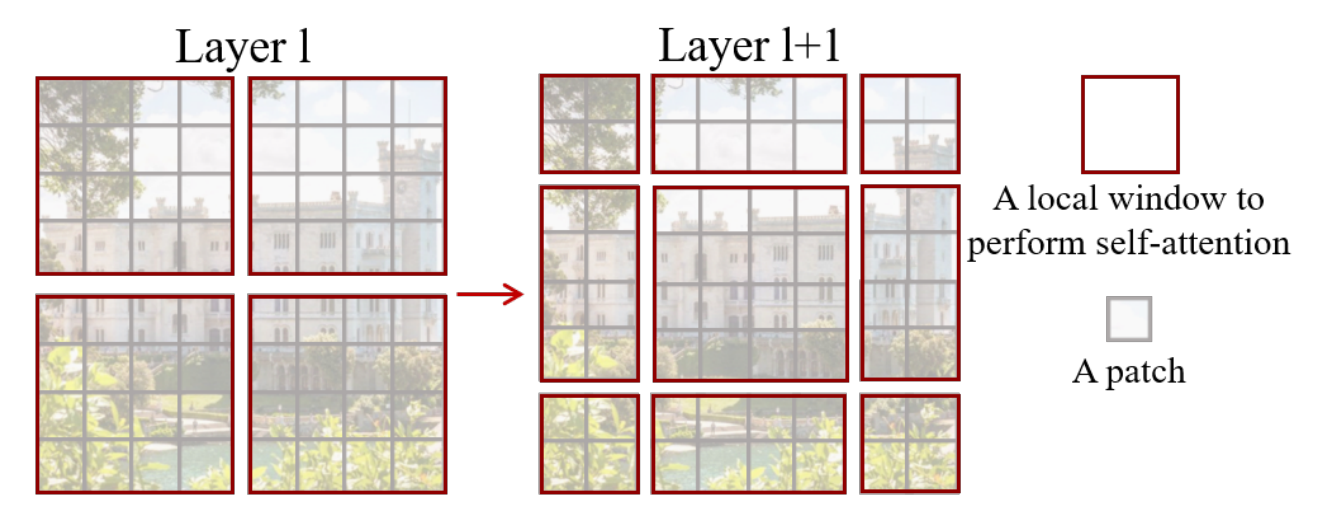
SWIN - 窗口移动

这种简化禁用了远距离补丁之间的信息流。为了解决这个问题，引入了窗口移动机制。
这种移动机制确保在连续层中注意力窗口被移动，从而通过多层实现信息流动。

通过移动窗口，其中一些将部分为空。尽管可以使用填充来填充这些窗口，但在这些移动操作期间循环滚动图像更为高效。

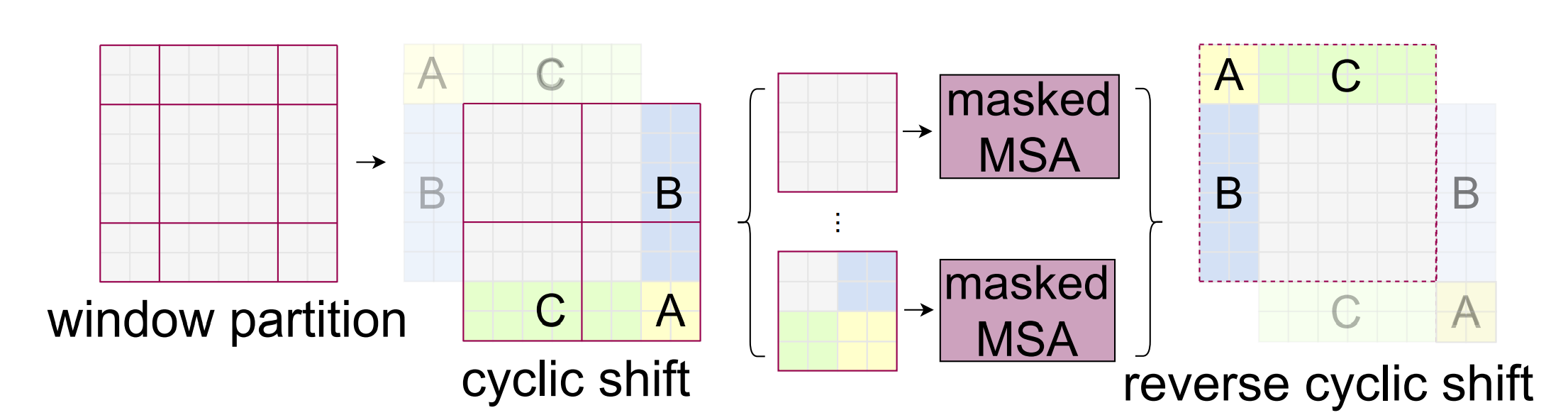
SWIN - 可学习的相对注意力偏差

作者发现，相对于绝对位置编码，一个简单的可学习偏差项更适合在注意力窗口中编码相对位置信息。

由于每个窗口是一个 $M \times M$ 的正方形，每个轴的相对位置在 $[-M+1, M-1]$ 范围内。因此，偏差矩阵的大小为 $[(2M-1)^2\cdot heads]$。$B$ 是从这个学习的矩阵中组装的，并应用于注意力中：

$$
O = softmax(QK^T/ \sqrt{d_k} + B)V
$$

在更高分辨率的输入情况下，使用双三次插值来上采样偏差矩阵。

分层 ViT 的优势

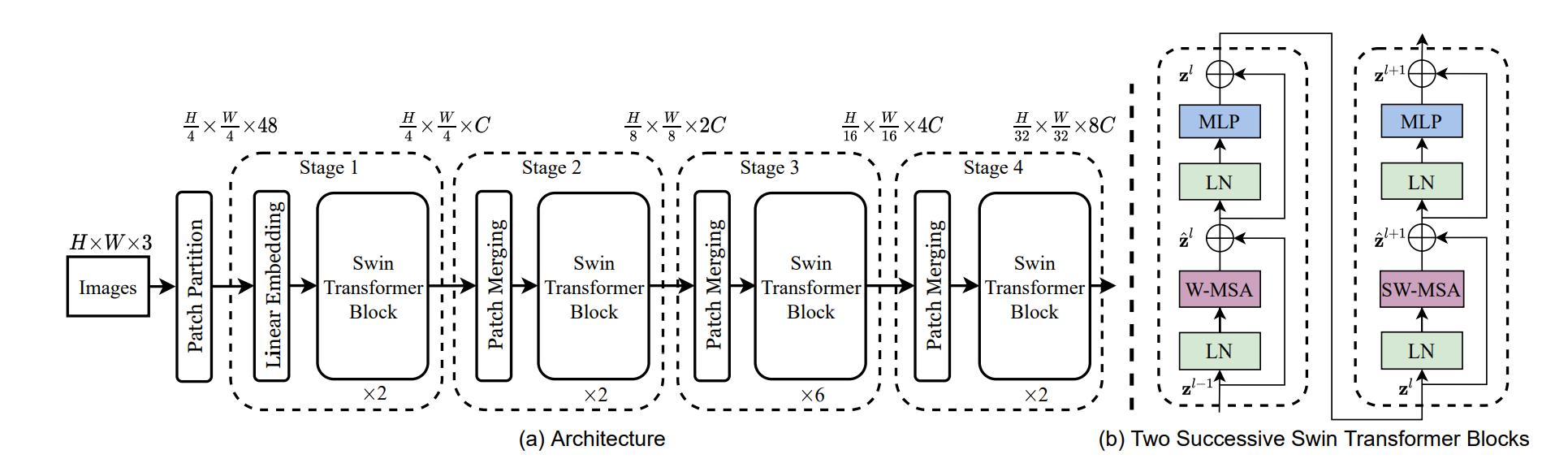
研究表明，这些分层 transformer 在性能和准确性方面比原始 ViT 提供了更高的组合。

学习通用表示

通用模型已经存在了一段时间（ImageNet 挑战等），这些模型的大规模预训练通常包括单一的分类任务。

然而，随着基础 transformer 表示模型的兴起，对更强预训练方法的需求也随之增加。通过额外的预训练任务，这些模型具有更好的泛化能力，甚至可能实现少样本学习。

迷你模型库

TrOCR

TrOCR 是一个简单的、基于 transformer 的编码器-解码器模型，执行 光学字符识别。

它基于原始的、完整的编码器-解码器 transformer 架构，由以下部分组成：

• 一个 视觉 transformer 作为编码器
• 一个 文本 transformer 作为解码器

编码器和解码器的权重均从预训练的单模态模型初始化，并在 OCR 特定的训练数据上进行预训练和微调。

TrOCR: 编码器

编码器将输入调整为固定大小，将其分解为补丁，并将每个展平的补丁线性投影到嵌入中。补丁的绝对空间位置由可学习的 1D (!) 位置嵌入表示。

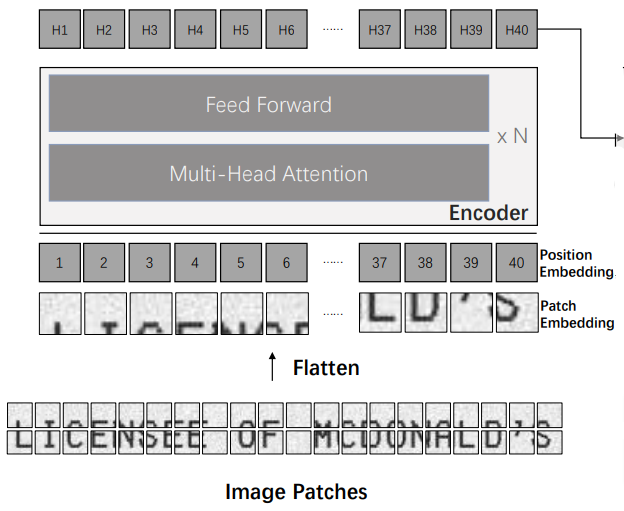
TrOCR: 解码器

解码器是一个标准的 transformer 解码器，交叉关注编码器的输出：

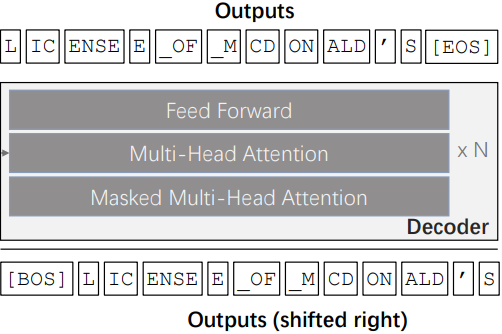
TrOCR: 初始化和训练

• 编码器权重使用预训练的视觉 transformer 权重（DeiT 或 BEiT）初始化
• 解码器权重使用仅解码器的 LLM 权重（RoBERTa 或 MiniLM）初始化，因此结构差异（大小、缺少交叉注意力）通过手动设置映射和随机初始化来处理
• 整个模型首先在一个非常大的合成数据集上进行 预训练，然后在较小的现实数据集上进行预训练
• 在下游任务上的最终测试是通过任务特定的微调完成的

LLaVA

LLaVA [大型语言和视觉助手] 是一个大型视觉语言模型，通过扩展一个指令微调的 LLM 以处理混合视觉和语言输入的多模态指令，从而训练用于 视觉指令跟随。

LLaVA 基于

• Vicuna，一个指令微调的 LLaMA，它是一个基于 transformer 解码器的 LLM
• 一个预训练的、基于 ViT 的 CLIP 图像编码器
• 一个可训练的投影矩阵，将视觉 CLIP 嵌入映射到 LLaMA 模型的词嵌入输入空间

在架构上，与 TrOCR 不同，LLaVA 并不是基于原始的完整 transformer 架构，因为解码器没有交叉关注编码的视觉输入，而是通过因果自注意力处理它。

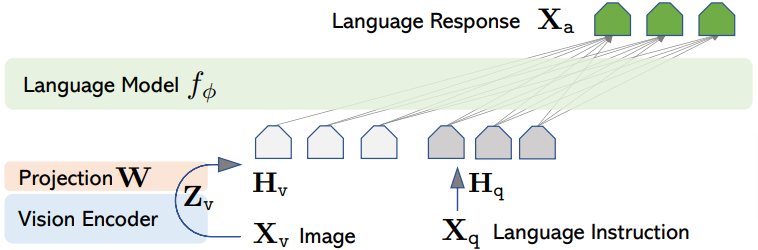
LLaVA: 数据集

视觉指令跟随数据集是使用仅语言的 GPT-4 作为强大的教师生成的：

• 视觉上下文始终是单个图像
• 图像的描述以两种形式提供：
  • 作为描述上下文图像的标题列表
  • 作为边界框坐标列表及其各自的类型

使用来自 COCO 数据集 的图像，GPT-4 被少样本提示生成

• 助手和用户之间关于图像的 对话
• 图像的 详细描述
• 基于图像的 深入逐步推理

LLaVA: 训练

通常，仅为示例的助手回答部分生成交叉熵损失。训练包括两个阶段：

• 预训练：首先，模型在 595K 图像-标题对上进行预训练，冻结 CLIP 编码器和 Vicuna 解码器，使用简单的图像描述指令上下文。这可以解释为训练投影矩阵成为 Vicuna 的视觉标记器
• 端到端微调：解冻 Vicuna 权重，并在 GPT-4 生成的 158K 多模态指令跟随数据集上联合微调投影矩阵和 LLM 权重

LLaVA 1.5

最近（2023 年 10 月），发布了一个新的改进版本 1.5 的 LLaVA，它目前是公共 VL 基准测试中表现最好的 VLM。更改相对较小：

• 使用 3 层感知器进行视觉语言映射，而不是线性投影
• 使用更大的 LLaMA 模型（13B 参数而不是 7B）
• 放大输入图像分辨率
• 提炼提示
• 在额外的学术 VQA 数据集上训练