NLP-TextImageModels
条件文本到图像模型
介绍
条件文本到图像生成
条件文本到图像生成是一项任务,其中模型被训练为根据给定的文本描述生成图像。
该任务可以通过以下方法之一来制定:
- 序列到序列 (seq2seq) 生成(与自回归 autoregression 的联系)
- 生成对抗网络 (GAN) 方法
- 自回归方法
- 扩散方法
序列到序列生成
2015年,DeepMind发布了DRAW,这是一个顺序的、无条件的图像生成模型。此类模型用于生成MNIST数据集等图像。
同年晚些时候,AlignDRAW发布了,这是DRAW的条件版本。它能够根据给定的文本描述生成图像。
AlignDRAW
AlignDRAW首先通过双向LSTM (BiLSTM)编码器将文本描述编码为潜在向量。然后解码器是一组“绘图”操作,尝试根据潜在向量生成图像。

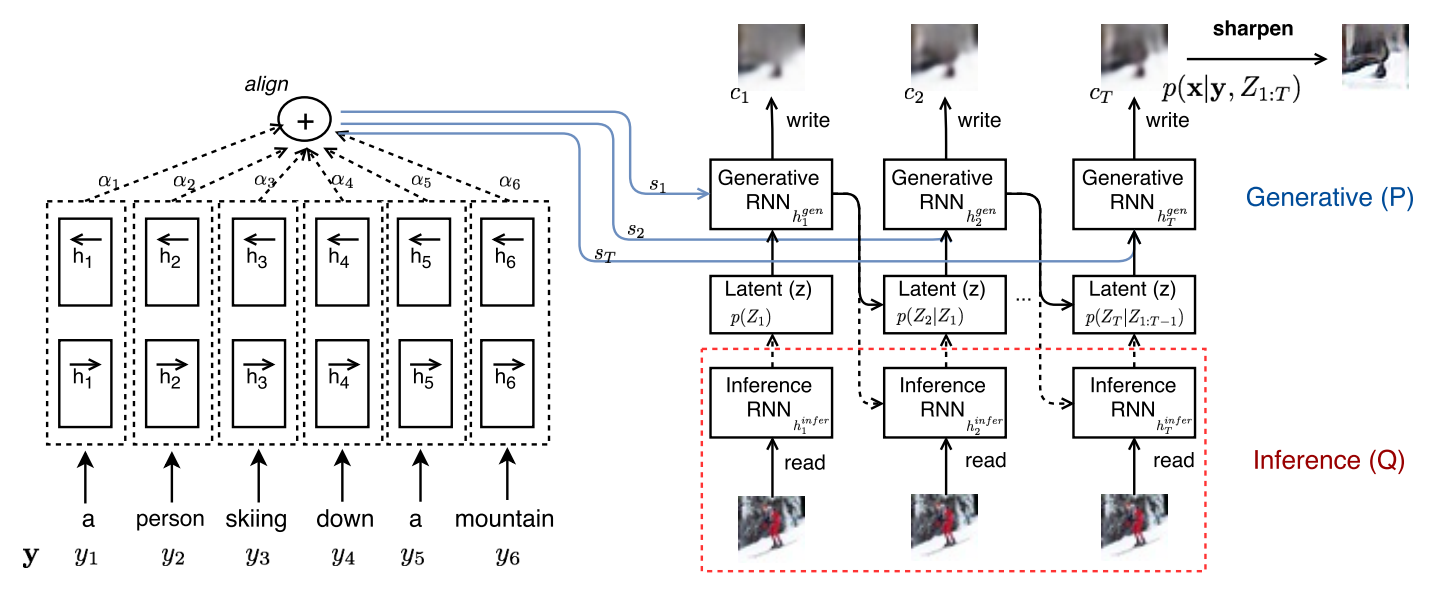
训练是变分下界 (ELBO) 优化(最大化)。
给定$x$,图像,$y$,文本描述,以及$Z$,一系列潜在向量,损失为:
$\mathcal{L} = \sum\limits_{Z}Q(Z|x,y)logP(x|y,Z)-D_{KL}(Q(Z|x,y)||P(Z|y))$
这里$Q(Z|x,y)$是近似后验分布。$P(x|y,Z)$是给定文本描述和潜在向量的图像的似然。$P(Z|y)$是给定文本描述的潜在向量的先验分布。
神经分布建模
$Q(Z_t|x,y,Z_{1:t-1})$ 和 $P(Z_t|Z_{1:t-1})$ 由高斯分布建模,分别基于推理和生成网络参数化。潜在变量以顺序方式相互依赖。
$P(Z_t|Z_{1:t-1}) = \mathcal{N}\left(\mu(h_{t-1}^{gen}),\sigma(h_{t-1}^{gen})\right)$
$Q(Z_t|x,y,Z_{1:t-1}) = \mathcal{N}\left(\mu(h_t^{infer}),\sigma(h_t^{infer})\right)$
$\mu(h) = tanh(W_{\mu}h)$
$\sigma(h) = exp\left(tanh(W_{\sigma}h)\right)$
读取和写入操作
读取和写入操作由不同大小、步幅和位置的固定高斯(模糊)滤波器组参数化。写入操作是滤波器组 ($F_x$, $F_y$) 和生成的 ($K$) 补丁的组合。
$write(h_t^{gen}) = F_x(h_t^{gen})K(h_t^{gen})F_y(h_t^{gen})^T$
而读取操作是该操作的逆操作。

GAN
生成对抗网络架构
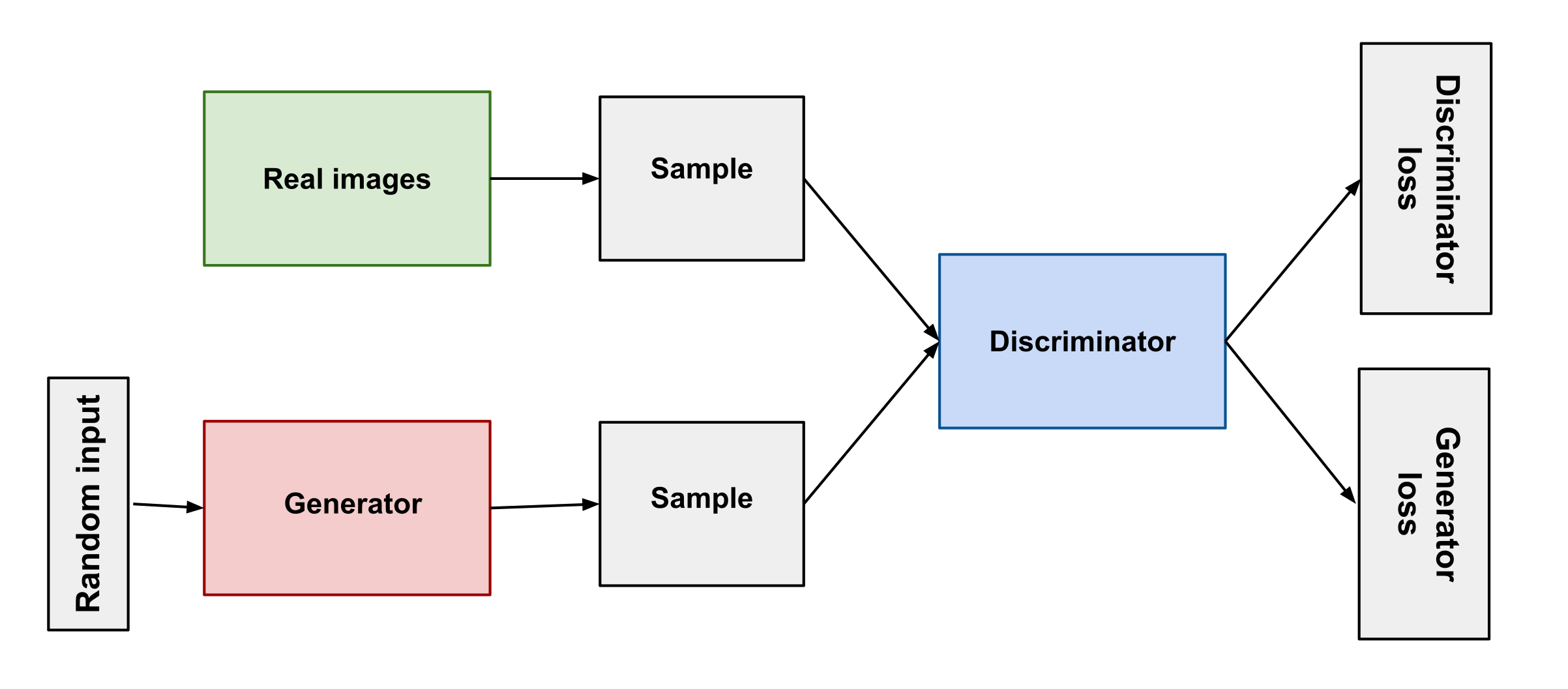
生成对抗网络回顾
GAN是一种生成模型,由两个网络组成:生成器和判别器。生成器尝试生成与真实数据集相似的数据,而判别器尝试区分真实数据和生成的数据点。
对抗游戏的目标如下:
因此,生成器尝试最大化 $log(D(G(z)))$,而判别器尝试最大化 $log(D(x)) + log(1-D(G(z)))$。
这里 $z$ 是从随机先验分布 $p(z)$ 中采样的,$x$ 是从真实数据分布 $p_{data}(x)$ 中采样的。
文本条件GAN架构
提出了一种文本条件GAN架构,该架构将文本编码作为潜在向量的一部分。该架构是一个反卷积-卷积网络。
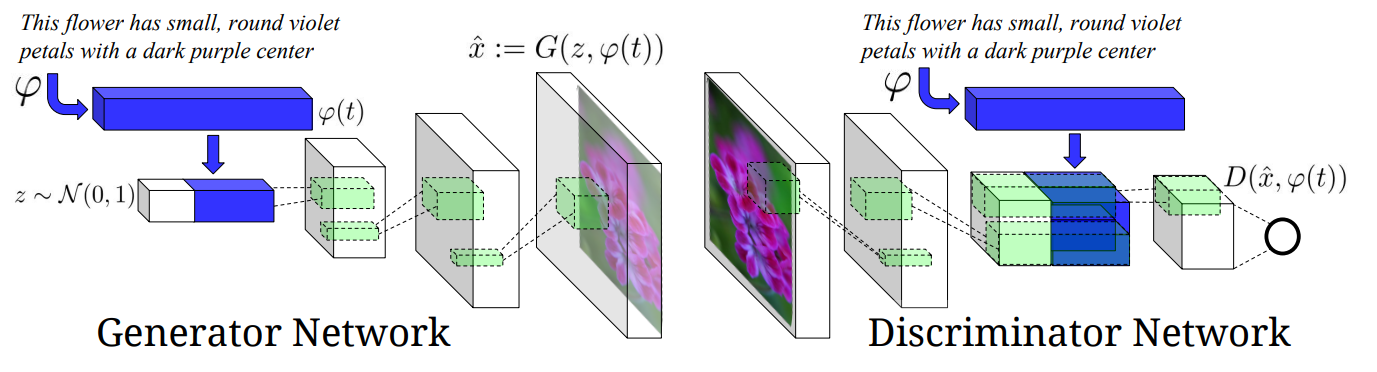
文本条件GAN训练
朴素GAN判别器任务:区分真实和虚假图像。
通过文本条件,我们获得了额外的任务:
- 拒绝任何文本描述的虚假图像。
- 拒绝不匹配的文本-图像对。
后者通过在每个训练批次中提供一组不匹配的示例来实现。
文本嵌入插值
由于当时文本-图像数据集稀疏,作者使用了一种文本嵌入插值方法来为未见过的文本描述生成更多的训练示例。这样,输入的文本嵌入是两个文本嵌入的线性组合。一个是正确的文本嵌入,另一个是数据集中的随机文本嵌入。然后将其传递给生成器。即使判别器没有给定对的真实示例,它仍然可以学习何时拒绝生成的图像。这增强了生成器。
作者建议对于 $t_1$ 和 $t_2$ 文本嵌入使用 $\beta=0.5$:
$D(G(z, t_1)) \rightarrow D(G(z, \beta t_1 + (1-\beta)t_2))$
文本条件GAN结果
文本输入:灰色的鸟有一个浅灰色的头和灰色的蹼足

风格编码
怀疑潜在变量应该包含文本中缺失但可以从图像(或一组图像)中推断的信息。他们称之为图像的“风格”,并提出了一种将此信息编码到潜在变量中的方法。
即他们提出了一种反转生成器的方法。$S(x)$ 通过以下目标进行训练,其中 $x$ 是图像:
$\mathcal{L}_{style}||z - S(G(z,t_1))||_2^2$
风格迁移推理过程如下:
$s \leftarrow S(x), \hat{x} \leftarrow G(s, t_1)$
风格编码结果

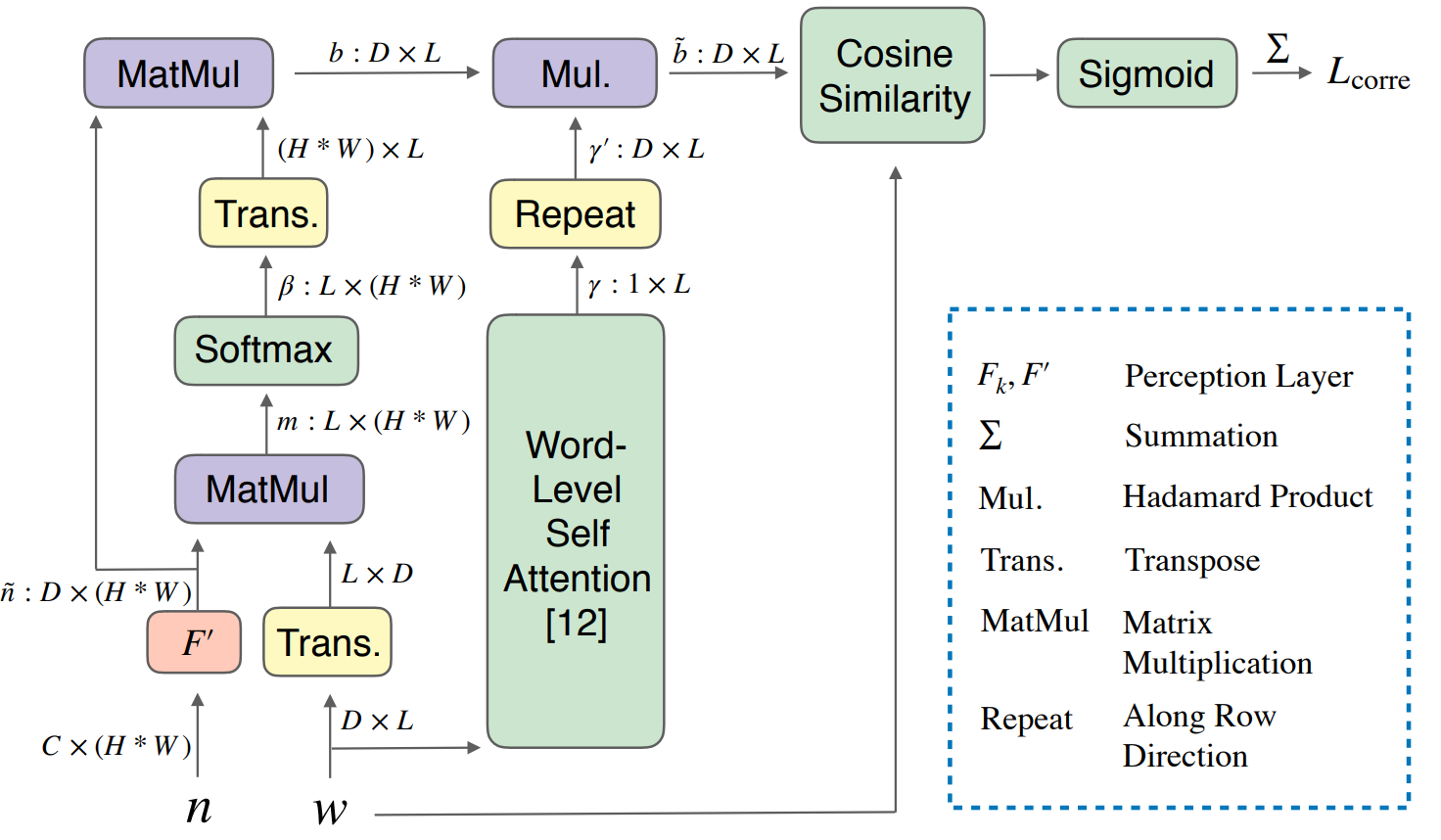
ControlGAN
ControlGAN 提供了一种细粒度的多阶段生成过程,并通过额外的监督方法来实现更好的结果。
他们添加了:
- 词和图像特征级别的判别器
- 多阶段生成和判别
- 无条件和条件损失、感知损失、词/图像特征级别的相关损失、文本到图像的余弦损失
- 定制的类似注意力机制
架构
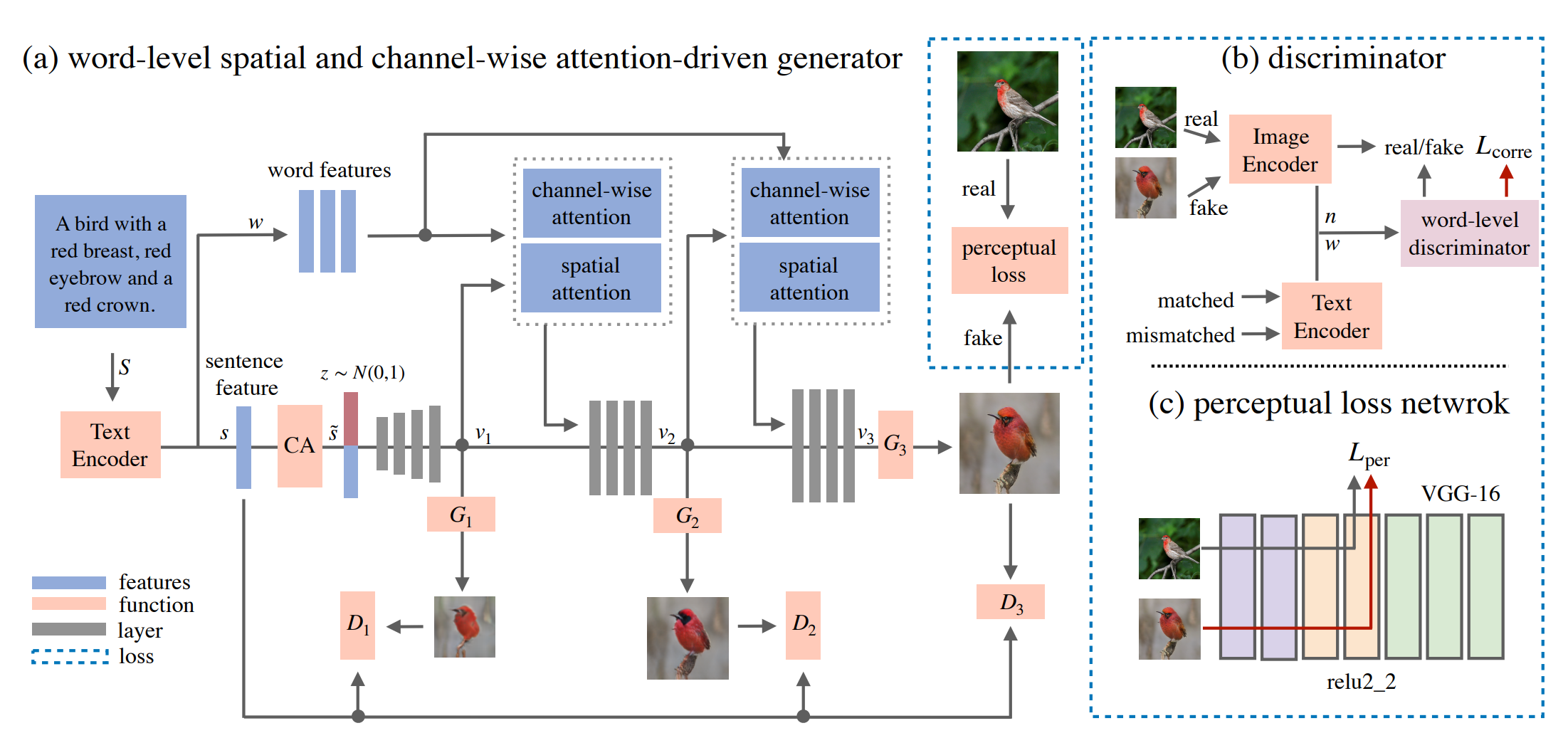
局部性

感知损失
感知损失用于生成一致的图像,包括未直接由文本引导的部分。这是通过使用预训练网络(在 ImageNet 上进行分类训练)来完成的。该网络用于从生成的图像和真实图像中提取特征。损失是特征之间的 L2 距离。特征从网络的中间层提取,以获得抽象但不太低级的表示。
$\mathcal{L}_{perceptual}^i(I, I’) = \frac{1}{C_iH_iW_i} ||\phi_i(I) - \phi_i(I’)||_2^2$
其中 $\phi_i$ 是特征提取器,$C_i$、$H_i$ 和 $W_i$ 分别是网络第 $i$ 层的通道数、高度和宽度。
词级特征
自回归方法
如果潜在先验包括文本条件,变分自编码器 (VAE) 也可用于根据文本描述创建图像。包括文本条件的一种方法是使用自回归先验模型。
这种自回归先验类似于语言建模中使用的自回归模型。不同之处在于词汇不仅是文本标记,还有使用与 VAE 相同表示的潜在图像特征。
图像编码和解码通常由 VAE 处理,而文本编码是自回归模型的一部分。
DALL-E 架构
DALL-E 训练
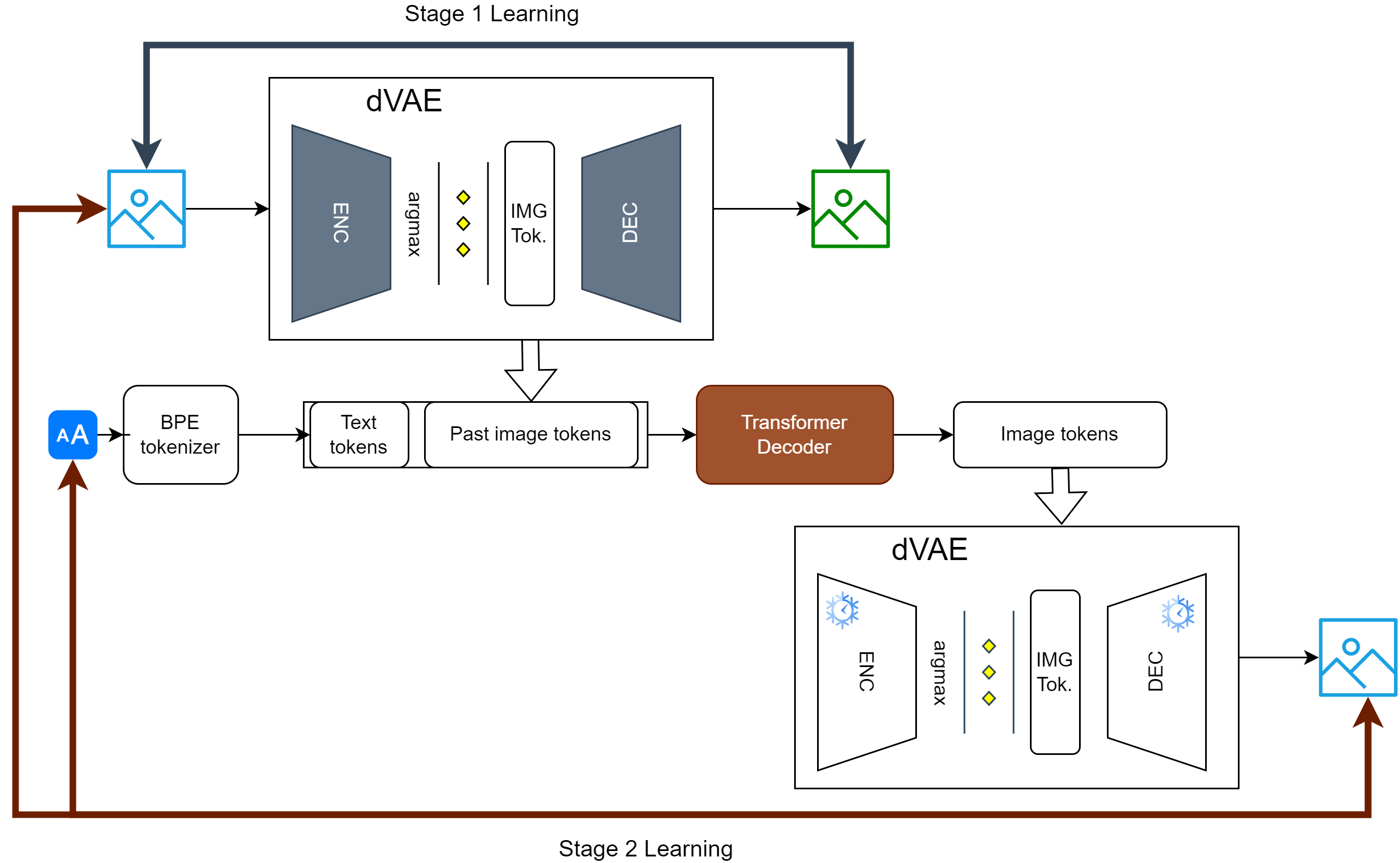
第一个 DALL-E 模型是基于变压器的自回归模型,使用 dVAE 进行编码,并使用稀疏变压器进行自回归潜在条件。
训练包括两个阶段:
首先,带有中间瓶颈块的 ResNet 风格 VAE 使用 ELBO 损失进行训练。潜在特征使用 argmax(贪婪采样)进行量化。此阶段的目标是图像重建。
这一阶段学习了一个约 8k 的视觉代码本(因为 dVAE 利用 argmax 进行量化),该代码本稍后在自回归模型中使用。
DALL-E dVAE 重建

DALL-E 自回归先验
在第二阶段,dVAE 权重被固定,解码器风格的潜在变压器被训练以学习条件先验。模型使用交叉熵损失进行训练,其中图像标记的权重是文本标记的 7 倍。
BPE 标记化的文本与特殊的填充标记(如果需要)和特定的 [START OF IMAGE] 标记连接在一起。然后将图像标记序列化并添加到末尾。文本具有 1D 位置编码,而图像标记具有单独的列和行位置编码。模型使用稀疏注意力来预测文本和图像的下一个标记。
DALL-E 注意力机制
文本标记具有因果注意力,而图像标记具有单独的行和列注意力,以及最后一层的 $3x3$ 局部注意力。列注意力被转置为行以减少计算量。行和列注意力以 (r, c, r, r) 的方式交替进行。

DALL-E 生成的图像
扩散方法
扩散模型
扩散模型是依赖于马尔可夫过程生成图像的高效模型。扩散由迭代的加噪和去噪过程定义。加噪是一个高斯噪声注入过程。维度不变。
](/AI/NLP/NLP-TextImageModels/diff_transform.png)
前向(编码)和反向(解码)扩散可以看作是 VAE 的等价物。
](/AI/NLP/NLP-TextImageModels/diffprocess.png)
DDPM
去噪扩散概率模型
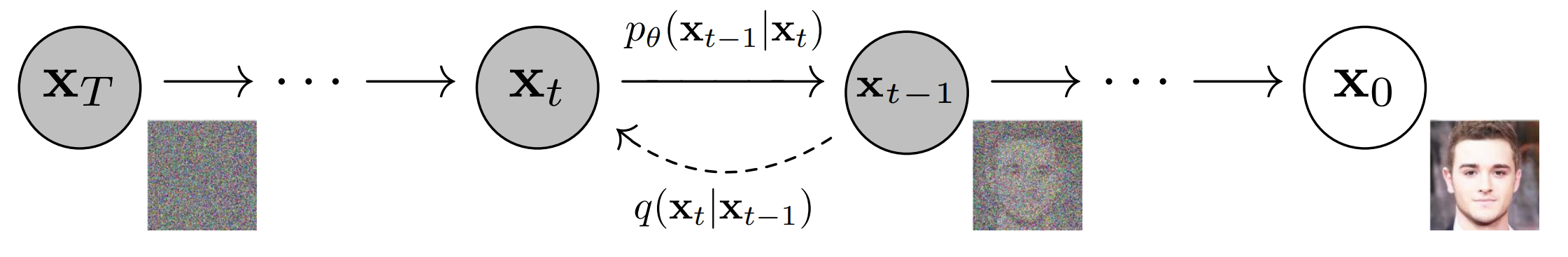
前向过程
$x_0$ 是起始图像,而 $x_T$ 是扩散过程的最终步骤 $t\in[0,…, T]$。
每一步 $q(x_t|x_{t-1})=\mathcal{N}(x_t;\sqrt{1-\beta_t}x_{t-1}, \beta_tI)$ 马尔可夫转移分布添加由固定 $\beta_t$ 调节的噪声。
反向过程
$x_T$ 从最终的 $p(x_T)=\mathcal{N}(x_T;0,I)$ 分布中采样。
每个反向步骤学习一个 $p_\theta(x_{t-1}|x_{t})=\mathcal{N}(x_{t-1};\mu_\theta, \Sigma_\theta)$ 高斯分布作为由 $\theta$ 参数化的转移。
两个马尔可夫过程在以下方程中建模:
$q(x_{1:T}|x_0)=\prod\limits_{t=1}^Tq(x_t|x_{t-1})$
$p_\theta(x_{0:T})=p(x_T)\prod\limits_{t=1}^Tp_\theta(x_{t-1}|x_t)$
给定 $\alpha_t = 1-\beta_t$ 和 $\bar\alpha_t=\prod\limits_{s=1}^t\alpha_s$,可以直接计算 $q(x_t|x_0)=\mathcal{N}(x_t;\sqrt{\bar\alpha_t}x_0,(1-\bar\alpha_t)I)$。这加速了训练,因为不需要递归。
学习反向过程
我们必须再次优化(作者取负并最小化)变分下界 $L = \sum\limits_{t=0}^TL_t$(直接应用计算的项):
这确保了第一个反向步骤接近最后一个前向步骤。
这里
是后验(贝叶斯后)分布,这是每一步的最优反向分布。
$L_0 = \mathbb{E}q(-logp\theta(x_0|x_1))$ 数据对潜在链末端的对数似然。
简化一切
有关训练目标推导的更多详细信息,请参见附录A。
如果我们固定两个过程的标准差并在每一步将它们绑定在一起(在每个高斯中使用 $\beta_tI$),则 $L_{t-1}$ 项回归到两个均值的距离。
$L_{1 \ldots t-1} = \mathbb{E}q\left(\frac{1}{2\sigma_t^2}||\tilde\mu(x_t,x_0)-\mu\theta(x_t, t)||^2\right) + C$
这里 $\tilde\mu(x_t,x_0)$ 是前向后验分布的均值(通过贝叶斯反转),而 $\mu_\theta(x_t, t)$ 是可学习的反向分布的均值。$C$ 是一个常数。
将重参数化技巧应用于 $q(x_t|x_0)=\mathcal{N}(x_t;\sqrt{\bar\alpha_t}x_0,(1-\bar\alpha_t)I)$ 我们得到:
$x_t = \sqrt{\bar\alpha_t}x_0 + \sqrt{1-\bar\alpha_t}\epsilon$ 其中 $\epsilon\sim\mathcal{N}(0,I)$
重新排列方程得到:$x_0 = \frac{x_t-\sqrt{1-\bar\alpha_t}\epsilon}{\sqrt{\bar\alpha_t}}$
贝叶斯后:$\tilde\mu(x_t,x_0)=\frac{\sqrt{\bar\alpha_{t-1}}\beta_t}{1-\bar\alpha_t}x_t+\frac{\sqrt{\alpha_t}(1-\alpha_{t-1})}{1-\bar\alpha_t}x_0$
替换 $x_0$ 我们得到:$\tilde\mu(x_t,\epsilon)=\frac{1}{\sqrt{\alpha_t}}\left(x_t - \frac{\beta_t}{\sqrt{1-\bar\alpha_t}}\epsilon\right)$
噪声预测
最后我们得出结论,为了最小化 KL 散度(通过近似 $\tilde\mu(x_t,x_0)$ 和 $\mu_\theta(x_t,t)$ 来最小化),我们必须预测 $\tilde\mu(x_t,x_0)$ 的未知部分,即 $\epsilon$,因为 $x_t$,$\alpha$ 和 $\beta$ 是已知的。为此,我们创建了一个 $\epsilon$ 的近似器,即 $\epsilon_\theta(x_t, t)$,因此 $\mu_\theta(x_t, \epsilon_\theta(x_t, t))=\frac{1}{\sqrt{\alpha_t}}\left(x_t - \frac{\beta_t}{\sqrt{1-\bar\alpha_t}}\epsilon_\theta\right)$。这可以在推理过程中使用。
如果我们忽略 $C$,$L_0$ 和 $L_T$,我们得到以下优化函数:
,在训练过程中我们使用第二种形式,因为 $x_0$ 和 $t$ 是输入。
训练和推理

总结
- 前向过程是一个马尔可夫过程,向图像添加噪声
- 我们可以直接计算前向过程的任意深度 $q(x_t|x_0)$
- 通过取前向过程的贝叶斯后验,我们有了反向过程的标签 $q(x_{t-1}|x_t,x_0)$
- 在推理过程中 $x_0$ 是未知的,因此我们需要一个不依赖于 $x_0$ 的反向后验近似器。这是 $p_\theta(x_{t-1}|x_t)$
- 优化目标是最小化(训练期间已知的)后验和近似后验之间的 KL 散度 $D_{KL}(q(x_{t-1}|x_t,x_0)||p_\theta(x_{t-1}|x_t))$
- 我们固定方差,因此只需通过 $\mu_\theta$ 近似均值
- 使用重参数化技巧,我们可以将不确定性分解为标准高斯噪声项 $\epsilon$,在 $x_0 \rightarrow x_t$ 转换过程中使用
- 这样 $\mu_\theta$ 的唯一非确定性部分是我们必须预测的 $\epsilon_\theta$。因此训练目标变为 $||\epsilon - \epsilon_\theta(x_t, t) ||^2$。其中 $\epsilon$ 是在前向过程中添加到图像的噪声项(训练期间可用)
特性
DDPM 使用小步长,累积约 500-1000 步生成。$\beta$ 的时间调度是线性的。作者使用相对较小的 $256\times256$ 尺寸的 U-Net 架构进行 $\epsilon_\theta$ 预测。

潜在插值
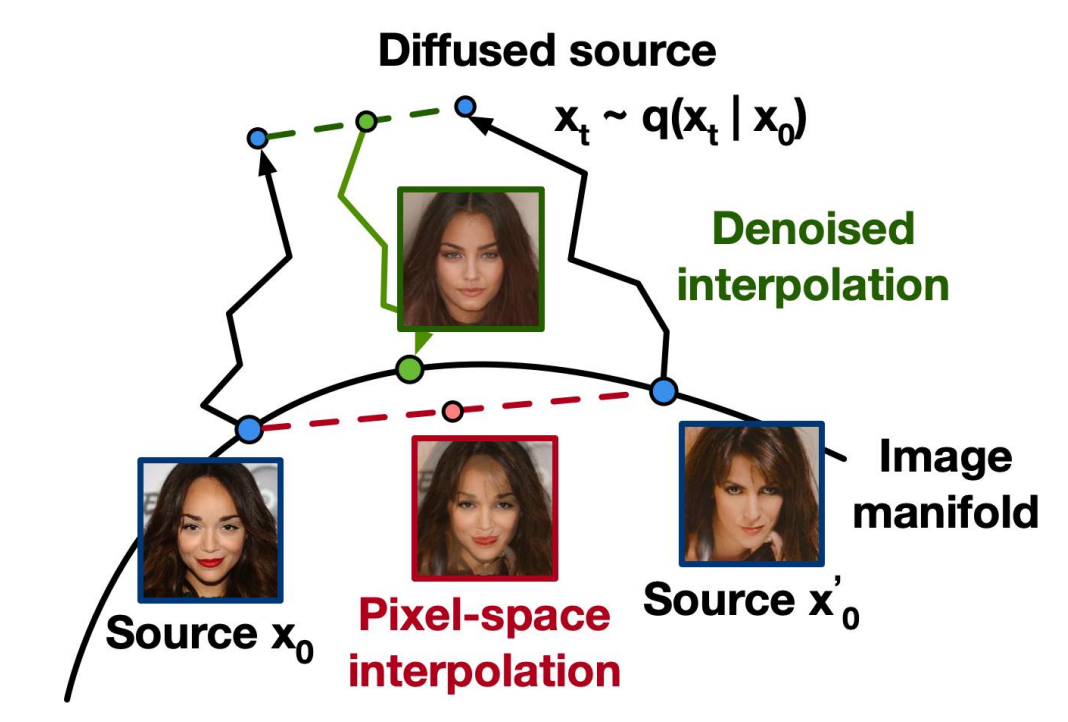

DDIM
去噪扩散隐式模型
DDPM 报告说,采样一批 $128$ 张 $256\times256$ 尺寸的图像大约需要 $300$ 秒。这是由于大量的小去噪步骤。
DDIM 通过放松马尔可夫约束并在前向和反向过程中制定隐式步骤来解决这个问题,从而使用更少的去噪步骤。
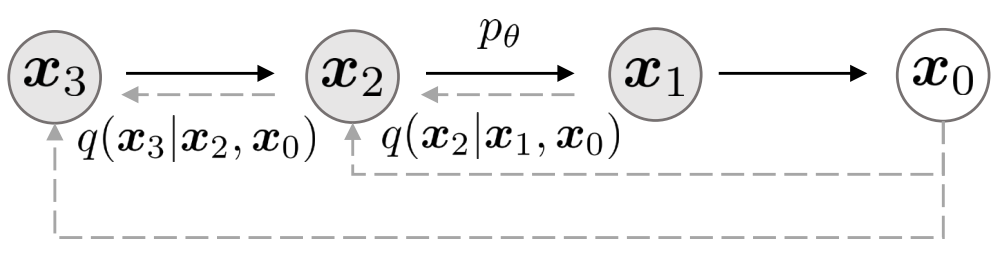
重新定义为非马尔可夫过程
在 DDPM 中,我们可以直接计算每一步的前向分布 $q(x_t|x_0)$。利用这一特性,我们可以在任何给定步骤 $t$ 直接计算 $L$,因为 DDPM 损失仅依赖于预测误差 $\epsilon_\theta(x_0, t)$。
DDIM 通过使用一个正系数向量 $\gamma$ 来权衡每一步的损失(由于 $t$ 仅影响添加的噪声 $\epsilon$,我们用 $\epsilon^t$ 表示 $t$ 依赖性):
通过将所有步骤的 $\gamma$ 固定为 1,我们得到原始的 DDPM 损失。
如果我们选择一组 $Q$ 前向分布,使它们可以边缘化为 DDPM 使用的相同 $q(x_t|x_0)$ 分布,我们得到相同的训练目标,因此可以使用相同的 DDPM 训练模型进行前向和反向过程,即使这些过程由于我们选择的 $Q$ 分布而是非马尔可夫的。
对于给定的正 $\sigma$ 标准差向量,存在这样的非马尔可夫过程。首先可以通过生成过程定义它。
$q_\sigma(x_{1:T}|x_0) = q_\sigma(x_T|x_0)\prod\limits_{t=2}^Tq_\sigma(x_{t-1}|x_{t},x_0)$
通过取 $q_\sigma(x_{t-1}|x_{t},x_0)$ 的后验(贝叶斯),我们得到 $q_\sigma(x_{t}|x_{t-1},x_0)$。通过对 $x_{t-1}$ 进行边缘化,我们得到 $q_\sigma(x_{t}|x_{0})$,因此我们可以使用($\gamma$)广义 DDPM 训练方案。
我们也可以重新定义反向过程 $p_\theta(x_{t-1}|x_t)$,它应该近似 $q_\sigma(x_{t-1}|x_{t},x_0)$。在生成过程中 $x_0$ 是未知的,但如果我们知道所有的误差 $\epsilon_t$,我们可以近似它。我们也有一个近似器 $\epsilon_\theta^t$。
让 $f_\theta(x_t)$ 通过从 $x_t$ 中减去适当缩放的误差近似 $\epsilon_\theta^t$ 来近似这个 $x_0$ 原始输入。
反向过程是 $p_\theta(x_{t-1}|x_t) = q_\sigma(x_{t-1}|x_t, f_\theta(x_t))$ 对于 $t>1$ 和 $\mathcal{N}(f_\theta(x_1), \sigma_1^2I)$ 对于 $t=1$。
优化目标可以表述为 ELBO,其中 $\simeq$ 用于描述等于一个不依赖于 $\theta$ 的常数,对于 $t>1$:
鉴于此,如果我们选择正确的 $\gamma$ 和 $C$ 项,我们将得到原始的 DDPM 损失。
反向过程
如果我们定义 $p_\theta(x_{t-1}|x_t) = q_\sigma(x_{t-1}|x_t, f_\theta(x_t))$ 并对其使用重参数化技巧(不包含详细信息),我们得到以下内容:
$x_{t-1} = \sqrt{\alpha_{t-1}}f_\theta(x_t)+\sqrt{1-\bar\alpha_{t-1}-\sigma_t^2}\epsilon_\theta^t + \sqrt{\sigma_t}\epsilon$
其中第一项是缩放的预测 $x_0$ 输入(也包括 $\epsilon_\theta^t$ 误差项),第二项是指向 $x_t$ 的“方向”,第三项是 $x_{t-1}$ 和 $x_t$ 之间的独立噪声差异。
如果我们为所有 $t$ 选择 $\sigma_t = \sqrt{(1-\bar\alpha_{t-1})/(1-\bar\alpha_t)}\sqrt{1-\bar\alpha_t/\bar\alpha_{t-1}}$,则前向过程变为马尔可夫过程,反向过程变为 DDPM。
如果 $\sigma_t = 0$,则前向过程在已知 $x_0$ 和 $x_{t-1}$ 的情况下变为确定性。反向过程将不包含独立噪声项,因此可以使用固定程序进行预测。
我们还可以通过超参数 $\eta$ 在两种版本之间进行插值:
$\sigma_t = \eta \sqrt{(1-\bar\alpha_{t-1})/(1-\bar\alpha_t)}\sqrt{1-\bar\alpha_t/\bar\alpha_{t-1}}$
加速生成
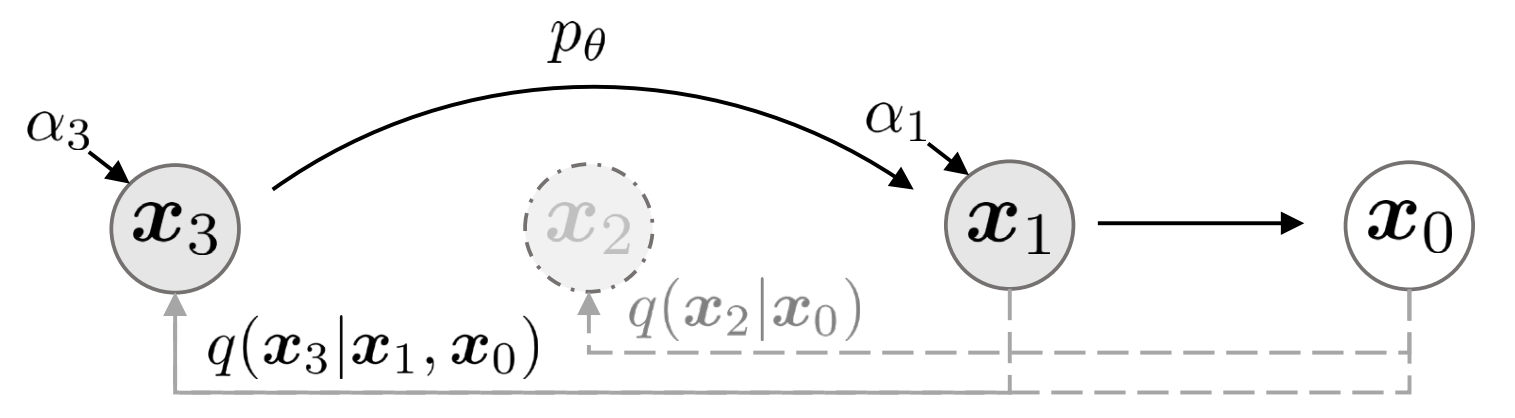
由于我们现在可以使用固定的反向过程(除了我们必须从 $x_t$ 预测 $x_0$),我们可以直接从任何一组 $x_t$ 中采样,包括跳过步骤或子采样步骤,甚至考虑基于连续时间的采样。
只要 $q_\sigma(x_{\tau_i}|x_{\tau_{i-1}},x_0)$ 是已知的,加速生成适用于一组步骤 $\tau_i \in [0, T]$,因为反向过程可以通过预测 $\epsilon_\theta^{\tau_i}$ 来近似 $q_\sigma(x_{\tau_{i-1}}|x_{\tau_i},x_0)$,这也用于 $f_\theta(x_{\tau_i})$。
重要的是,仅通过近似 $\epsilon_\theta^t$ 才能实现这种采样步骤的重新调度(至少在 DDIM $\eta=0$ 的情况下),因为我们可以在数学上解释这些变化。
这样,采样不再与训练(前向)步骤数绑定,可以实现大约 $10-50$ 倍的加速生成,从而促进在接近实时应用中使用更大的模型。
结果

超越 DDIM
通过将 DDIM 重新表述为 ODE 求解器(常微分方程),得出它等效于 ODE 求解的欧拉方法。还可以使用其他扩展的 ODE 求解器,例如 DPM++。到 2023 年底,这些是最流行的扩散采样器。在更高阶 ODE 求解器领域也有一些研究,但尚未观察到广泛使用。
还提出了超越 DDPM 和 DDIM 使用的线性 $\beta$ 的新噪声调度方法。
DDIM 总结
- DDIM 使用非马尔可夫过程进行扩散,使用跳到 $T$ 的想法,然后逐渐反转到 $t$。$q_\sigma(x_{1:T}|x_0) = q_\sigma(x_T|x_0)\prod\limits_{t=2}^Tq_\sigma(x_{t-1}|x_{t},x_0)$
- 然后反向过程可以直接使用 $q_\sigma(x_{t-1}|x_t,x_0)$。这里 $x_0$ 仅在训练期间已知,因此在推理过程中我们必须使用预测器来近似它,而不是像在 DDPM 中那样近似完整的后验
- 我们定义 $f_\theta(x_t)$ 从 $x_t$ 近似 $x_0$,并使用相同的表示技巧将问题转化为噪声 $\epsilon$ 预测问题
- 证明了 DDIM 和 DDPM 的训练目标是等效的,只是包围误差预测的数学结构不同
- DDIM 推理过程实现了 $x_t \rightarrow f_\theta(x_t) \rightarrow x_0 \rightarrow x_{t-1}$ 的直觉。注意 $t-1$ 预测不显式依赖于 $t$,因此我们可以跳到任何先前的步骤而不是 $t-1$
- 然而,$f_\theta(x_t)$ 预测并不完美,因此反向过程也应该采取多个步骤的细化以确保一致的质量
- 现代实现将时间步长处理为连续变量,因此它们使用 ODE 求解器来指导反向过程
引导扩散
分类器
扩散引导也可以类似于文本依赖的GAN和VAE。在这种情况下,我们的扩散模型的估计器应该受到引导信号(例如文本嵌入)的扰动。
在反向过程中,给定噪声估计器 $\epsilon_\theta$,我们将条件偏移加到噪声项的估计中。
$\hat\epsilon_\theta(x_t,y) = \epsilon_\theta(x_t,y) + s\sigma_t \nabla_{x_t}logp_\phi(y|x_t)$
其中$s$是引导尺度,$p_\phi(y|x_t)$ 是一个分类器,使用关于我们想生成的类别的对数似然的导数来引导扩散过程。
无分类器
这需要扩散模型与分类器一起训练,并且在生成过程中也需要分类器梯度。为了避免这种情况,无分类器网络在无条件估计器 $\epsilon_\theta(x_t)$ 和条件估计器 $\epsilon_\theta(x_t,y)$ 上操作,通过与无条件预测的差异来实现 $\hat\epsilon_\theta(x_t,y) = \epsilon_\theta(x_t,y) + s(\epsilon_\theta(x_t,y)-\epsilon_\theta(x_t))$
这本质上是通过在训练期间向分类器添加$0$标签来完成的,因此无分类器估计器只是 $\epsilon_\theta(x_t,0)$。
CLIP引导扩散: GLIDE
引入了一种方法,用CLIP点积相似度度量替换分类器。
$\hat\epsilon_\theta(x_t,y) = \epsilon_\theta(x_t,y) + s\sigma_t \nabla_{x_t}(f(x_t)\cdot g(y))$
这里$f$是图像编码器,$g$是文本编码器。重要的是,这个CLIP版本是用噪声图像训练的,以匹配扩散模型的噪声水平。
还得出结论,无分类器引导在小众任务上似乎比CLIP引导更有效。这里文本由类似GPT的模型编码,利用最后的嵌入向量。
GLIDE结果

潜在扩散
潜在扩散是指在VAE或GAN的潜在空间中进行扩散的方法。DALL-E 2和Stable Diffusion是这种方法的两个流行示例。
虽然DALL-E 2使用类似CLIP的模型作为VAE,并具有基于Transformer的扩散先验,但Stable Diffusion利用VQ-GAN生成器和U-Net风格的先验。
DALL-E 2
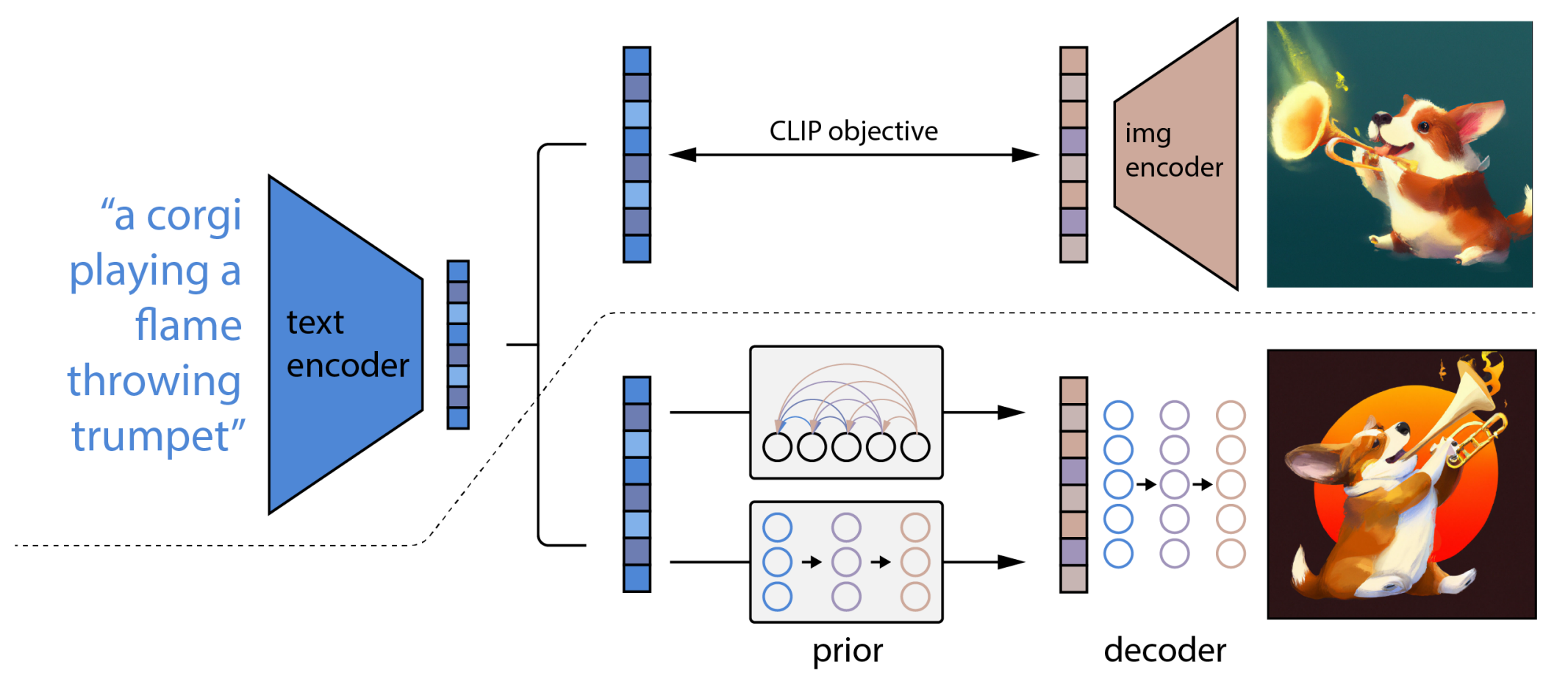
解码器
DALL-E 2 包含一个由 CLIP 文本编码器构建的 VAE 和一个用作图像解码器的扩散模型(因此 OpenAI 也将 DALL-E 2 背后的模型命名为“unCLIP”)。该解码器以 CLIP 图像嵌入为条件,也可以选择以字幕文本嵌入为条件。它使用 GLIDE 的架构,并通过在解码器训练期间偶尔丢弃 CLIP 嵌入和字幕嵌入来包括一些无分类器的改进。
训练使用锐度感知最小化。
解码器在 DDIM 过程中使用 $\eta>0$ 以允许生成图像的变化。
先验
他们比较的 VAE 先验是 DALL-E(1)风格的自回归先验和扩散先验,后者被证明更优越。扩散过程也使用 Transformer 解码器来预测下一个潜在标记版本。损失不是基于 $\epsilon$ 的,而是预测和真实潜在表示之间的 L2 损失。这被解释为扩散过程中由 $f_\theta(x_t, t, y)$ 参数化的预测 $x_0$ 的损失。
在生成过程中,先验生成两次,选择与文本嵌入点积较高的那个。
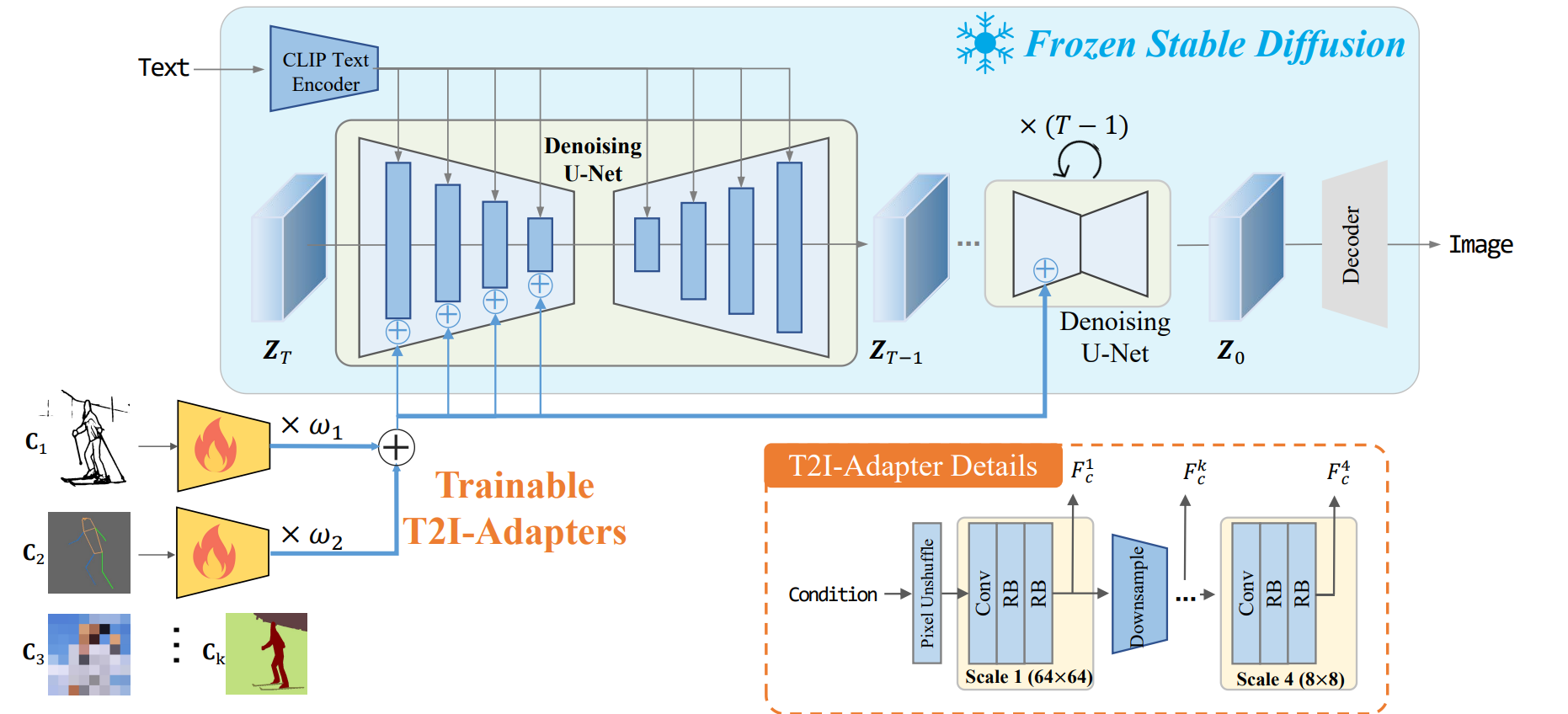
Stable Diffusion
SD 架构
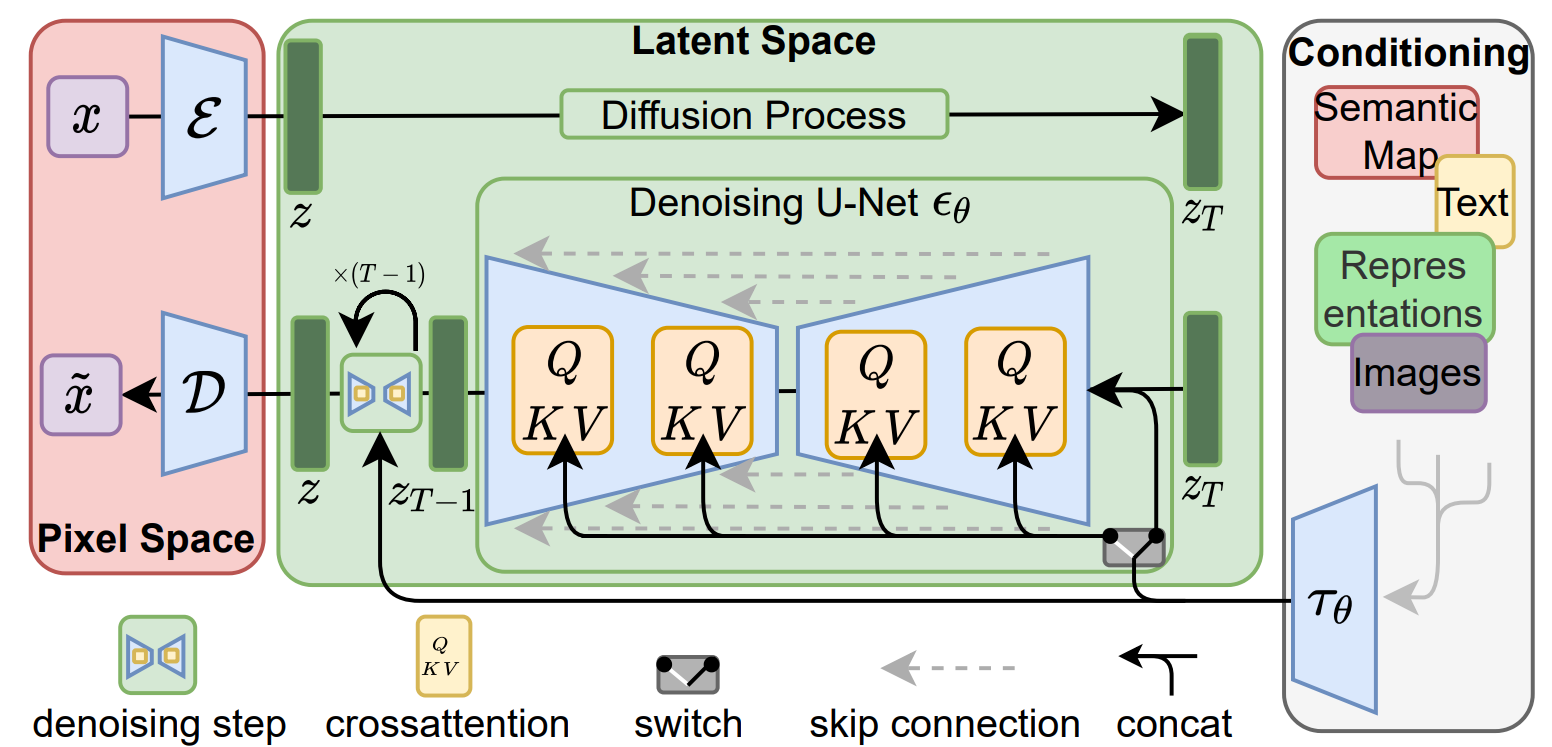
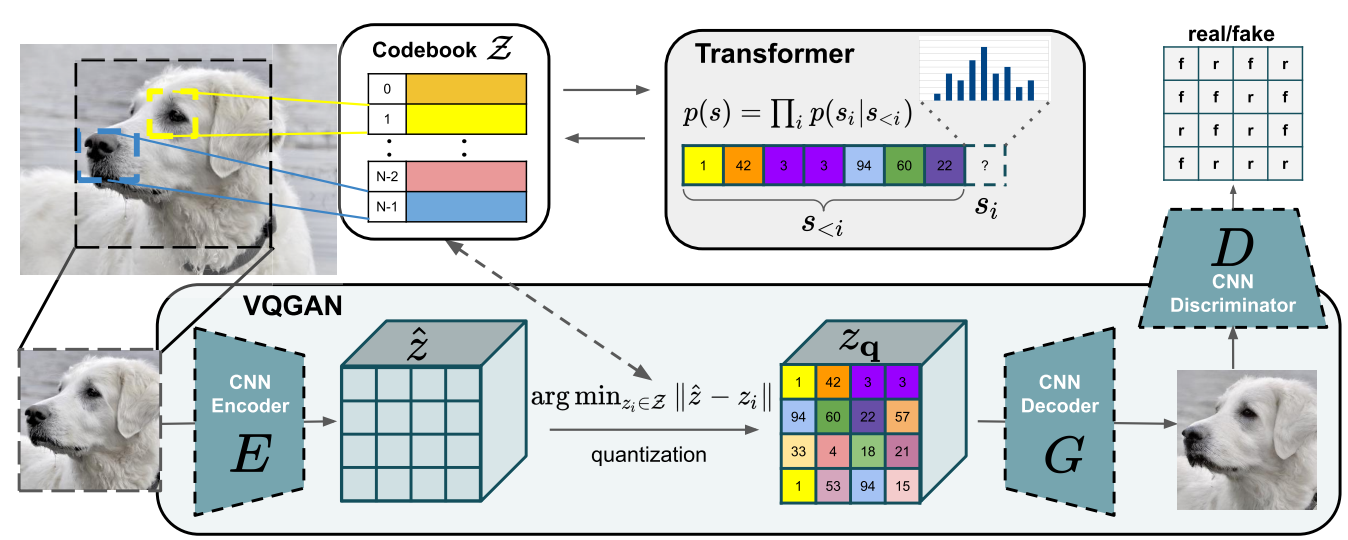
VQ-GAN
在 Stable Diffusion 中,为了将图像投影到潜在空间,使用 VQ-GAN 对图像进行编码。VQ-GAN 由 VQ-VAE 生成器和对抗性和感知损失的判别器组成。在 Stable Diffusion 的情况下,VQ-VAE 得到轻微的 KL 散度正则化,以生成更接近高斯分布的潜在表示。
此外,判别器后来被忽略,只使用生成器 VQ-VAE,以一种将量化与解码器合并的方式使用。使用 2D 表示的压缩因子 $4-8$ 被发现表现最佳。
SD 先验
先验本身是一个卷积 U-Net 架构,每一层都有交叉注意力块。这些交叉注意力关注于编码的条件模态。这个 U-Net 执行反向扩散过程(预测 $\epsilon_\theta$)。
作为条件编码的模态可以是文本(transformer-decoder 或 CLIP)、图像、分割掩码等……甚至低分辨率图像也可以用来构建潜在的超分辨率模型。无分类器引导也被探索并且有益。
这是一个潜在扩散,这意味着名称 LDM(潜在扩散模型),它是 Stable Diffusion 中使用的模型的泛化。
零样本

放大

分割掩码合成

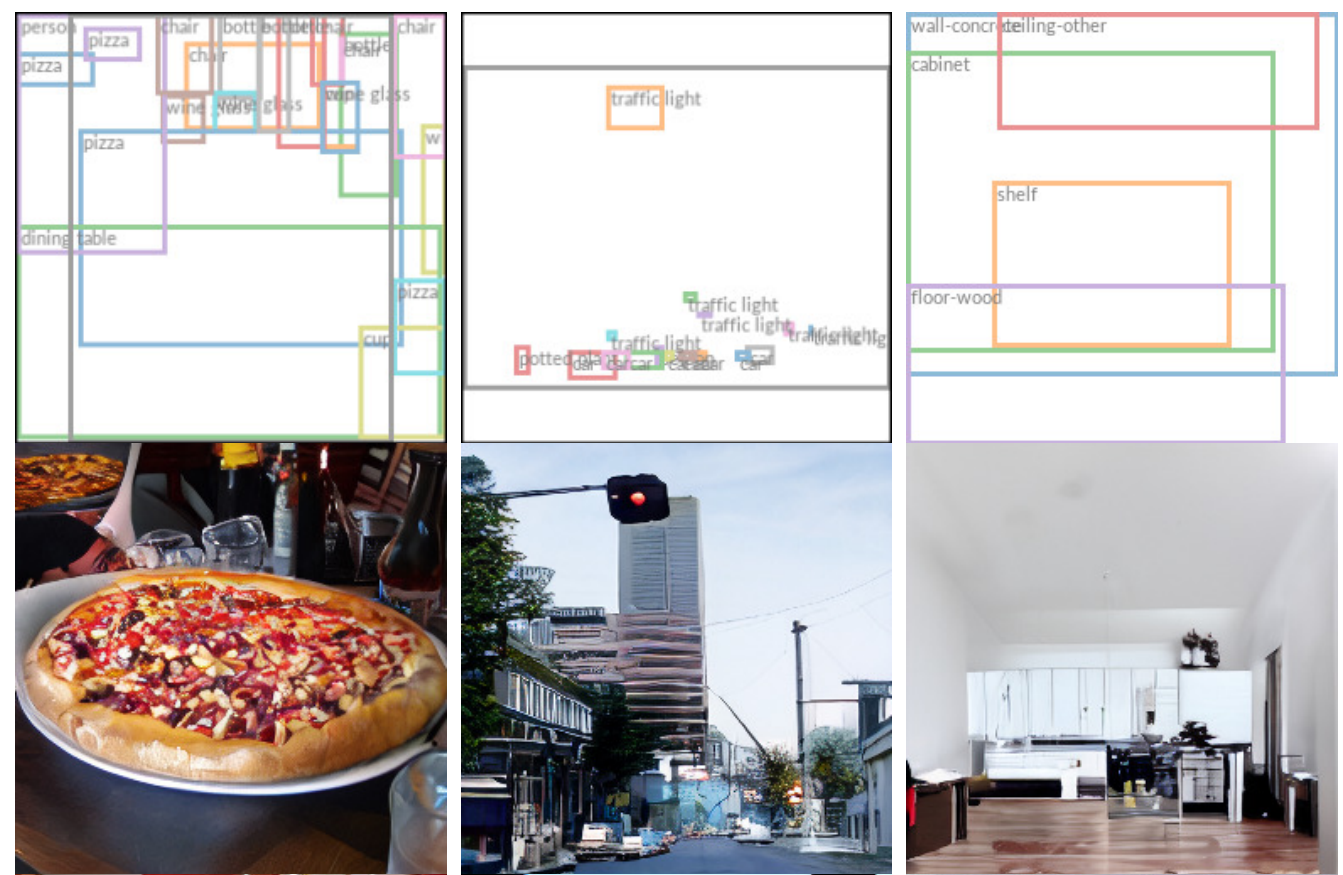
布局合成
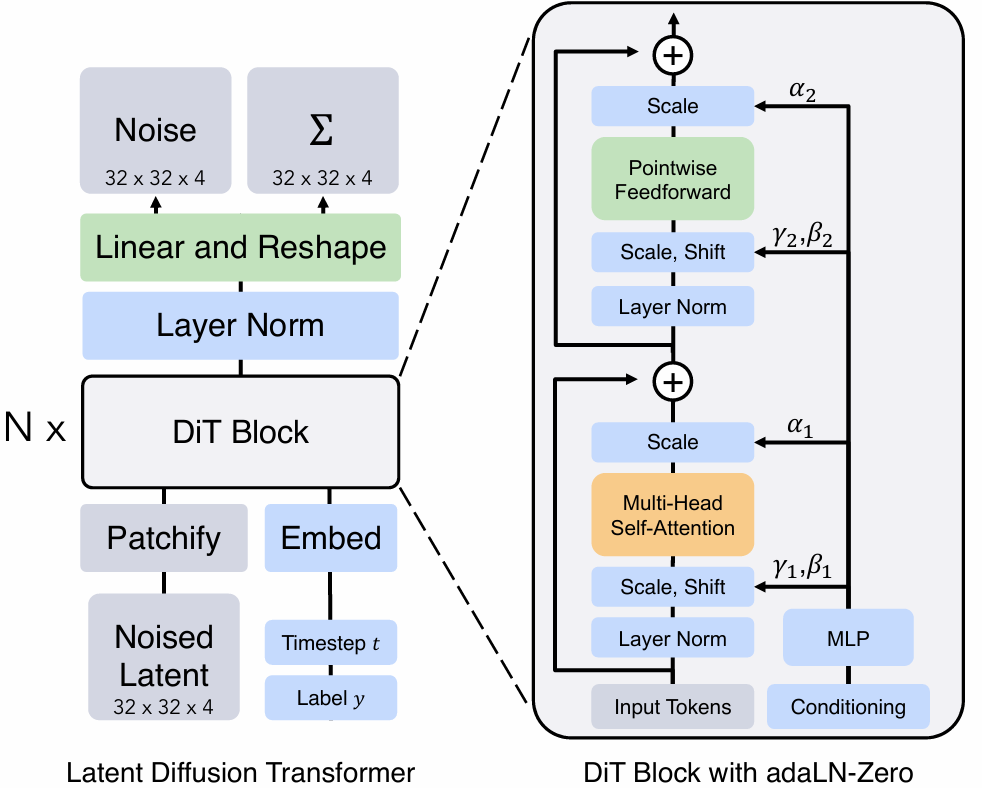
DiT
在一些最近的模型中,UNet 被一种特殊的扩散变压器 (DiT) 架构所取代,该架构使用类似 ViT 的主干,并通过条件输入来预测误差图像(在某些情况下甚至是复杂扩散用例中使用的 $\Sigma$ 协方差)。
这样,DiT 的输出是两个预测的“图像”(如 UNet 的情况)——误差和协方差,它们通过线性层和补丁过程的逆过程从输出标记中组装而成。
作者观察到,与卷积 UNet 相比,该模型具有更好的扩展性。
条件
还探索了注入条件的最佳方式。他们发现自适应层归一化是最佳解决方案,具有零缩放初始化(因此在开始时只有残差是活跃的)。
这意味着条件信号通过 MLP 映射到潜在大小,MLP 发出输入缩放、输出缩放和我们应用于变压器数据流的移位值。
作者还指出,这优于上下文内条件、交叉注意力,甚至是具有非零缩放初始化的自适应层归一化。
DiT 架构
扩散模型的扩展
多阶段网络
多阶段网络用于提高扩散和潜在扩散模型的效率。DALL-E 2 在像素空间中使用多阶段扩散,结合基于 CLIP + 字幕的文本条件超分辨率模型。DALL-E 3 论文还提到他们在不同分辨率上使用了三阶段扩散模型。细节未披露。
最新的发展还引入了精炼器,这些精炼器经过训练以提高生成图像的细节和一致性(整体质量)。这些精炼器在高质量图像上进行训练,并在生成原始潜在图像后使用。

Imagen 在先验扩散上使用仅文本条件,然后在像素空间中进行两个文本条件超分辨率。
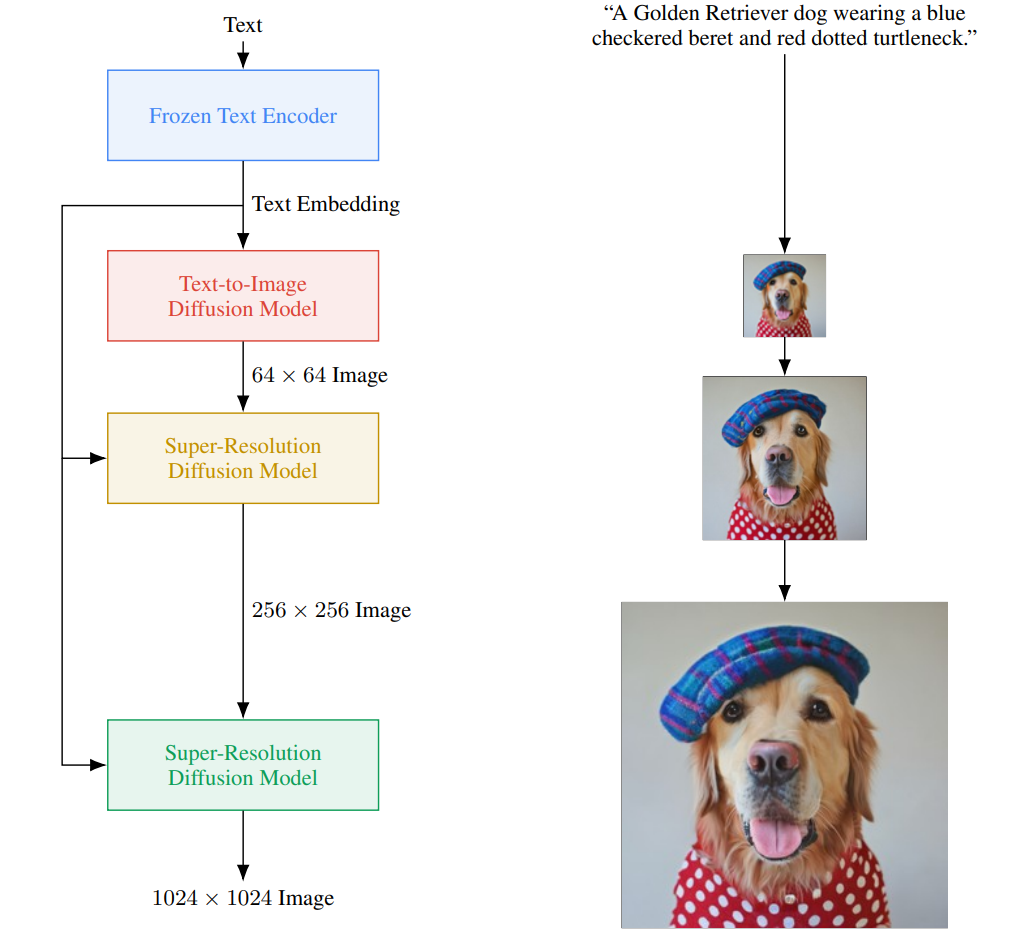
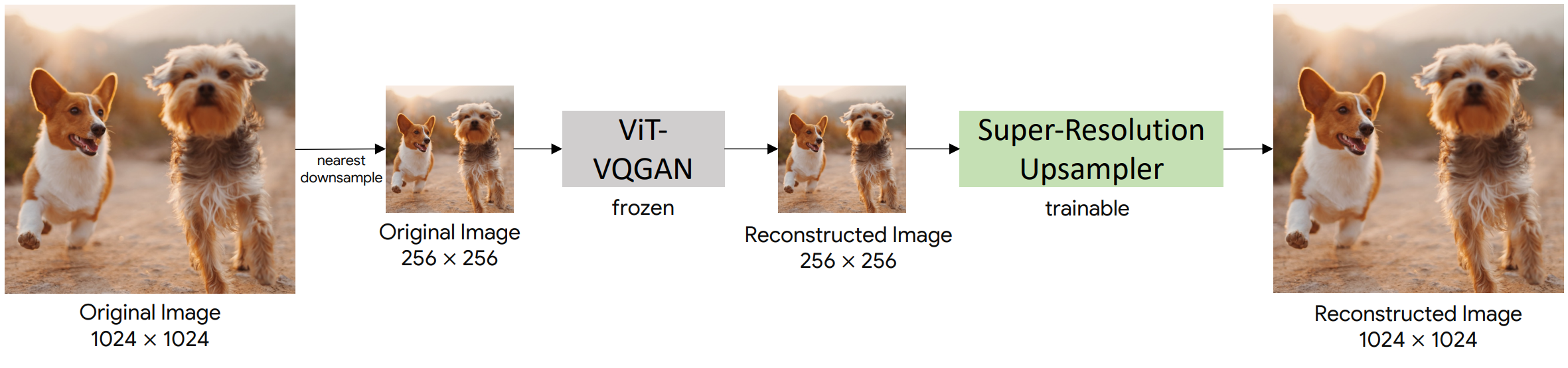
自回归模型也可以以多阶段方式使用。例如,Parti 由 ViT-VQ-GAN 标记器和解码器组成,用于编码和解码图像。自回归模型是一个全栈变压器,其中条件被编码并生成图像。
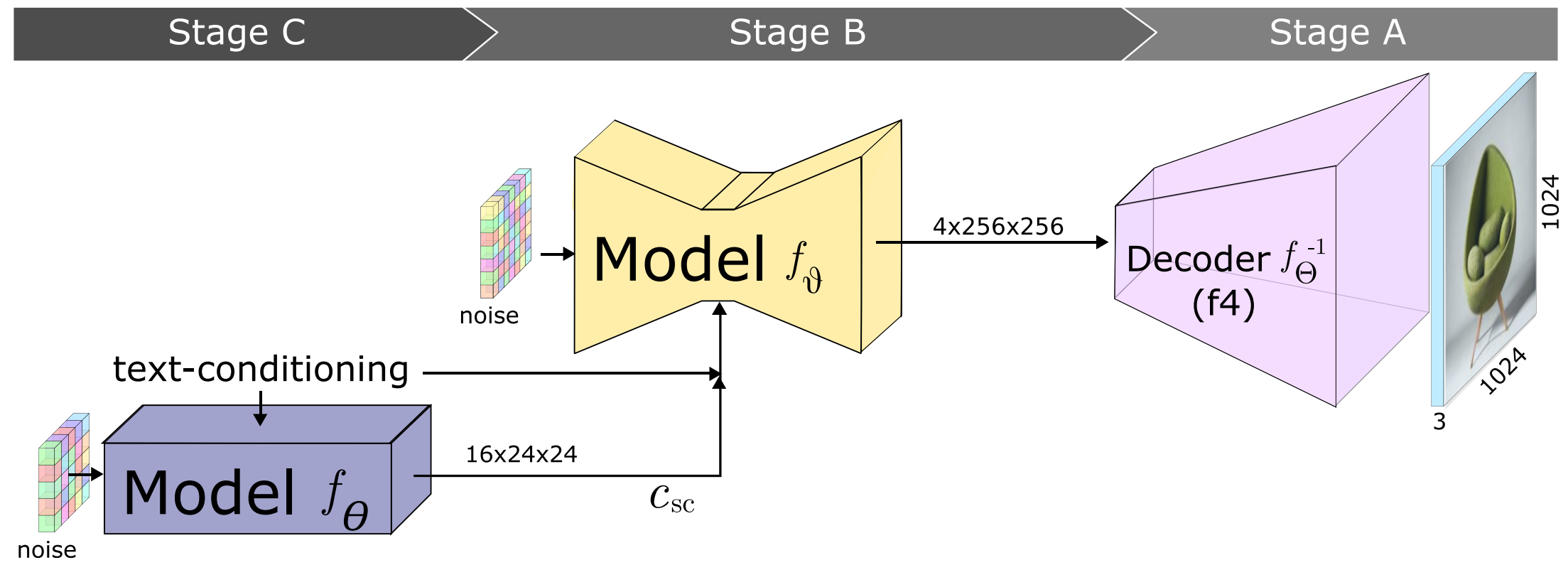
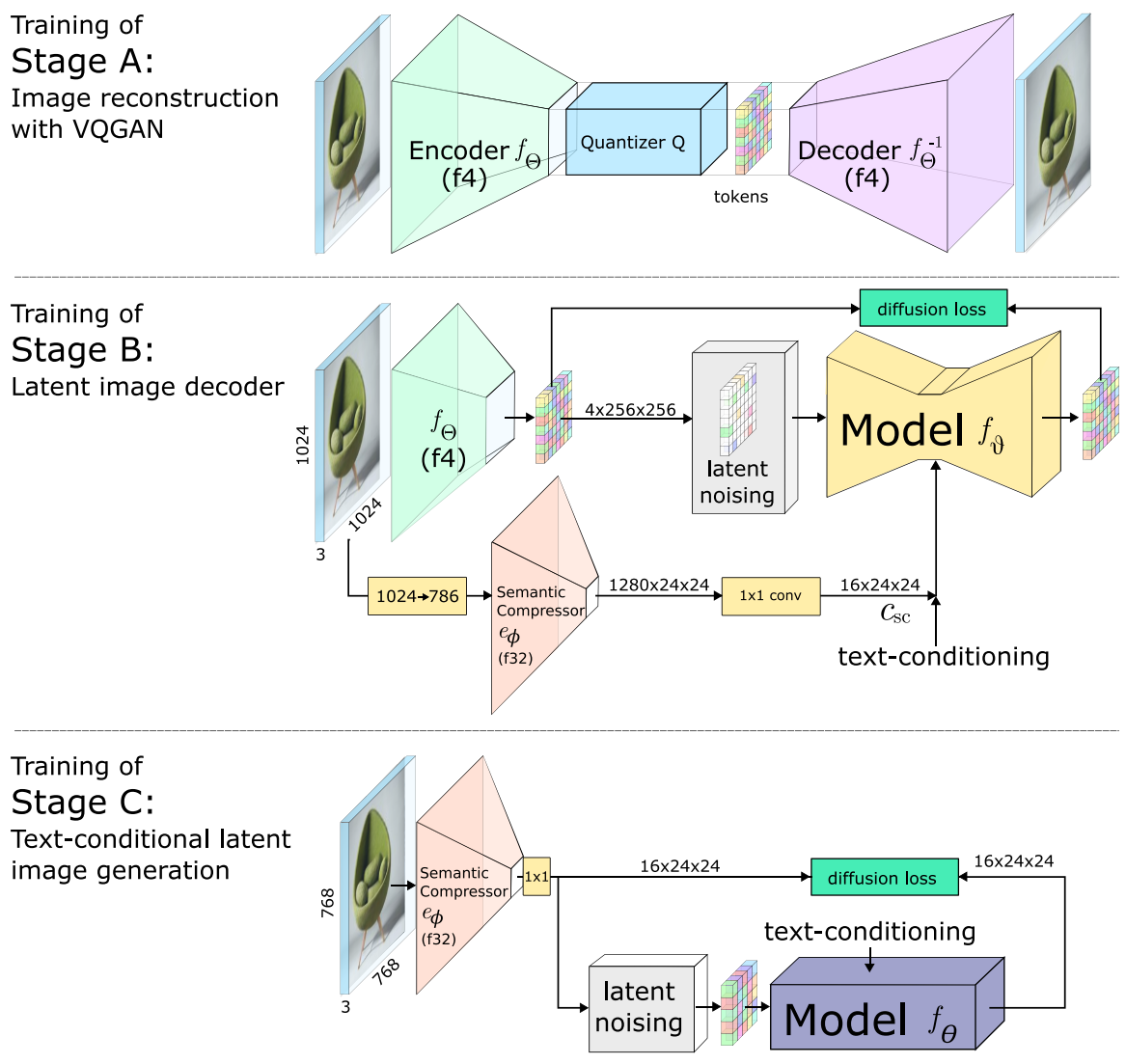
最近的升级,Würstchen 是一种潜在模型,使用类似于 Stable Diffusion 的 VQ-GAN 生成器(即 VQ-VAE)的编码器-解码器架构,但量化后来被放弃。先验是一个多阶段扩散模型,在高度压缩步骤上使用仅文本条件,然后将此压缩潜在先验和文本用作潜在上采样器的条件步骤,生成最终先验。
修复
修复是通过用生成的部分替换原始图像的部分(无论是在像素空间还是潜在空间)来实现的。这是通过使用用户提供的掩码来完成的。在扩散过程中,在扩散过程的每一步中使用未掩盖部分的充分加噪版本。掩盖部分通过加噪的原始 $x_0 \rightarrow x_T$ 或生成的随机初始值进行初始化。

文本反演
文本反演用于扩展文本到图像模型的功能。它们在一小组图像上进行训练,这些图像被输入到预训练的文本到图像模型中。模型被冻结,除了文本编码器的嵌入层。这个嵌入层通过一小组嵌入向量(可以不止一个)进行扩展,这些嵌入向量在一小组图像的扩散损失上进行训练。这样,模型就学会了生成具有新添加的嵌入向量中编码的相同对象或风格的图像。

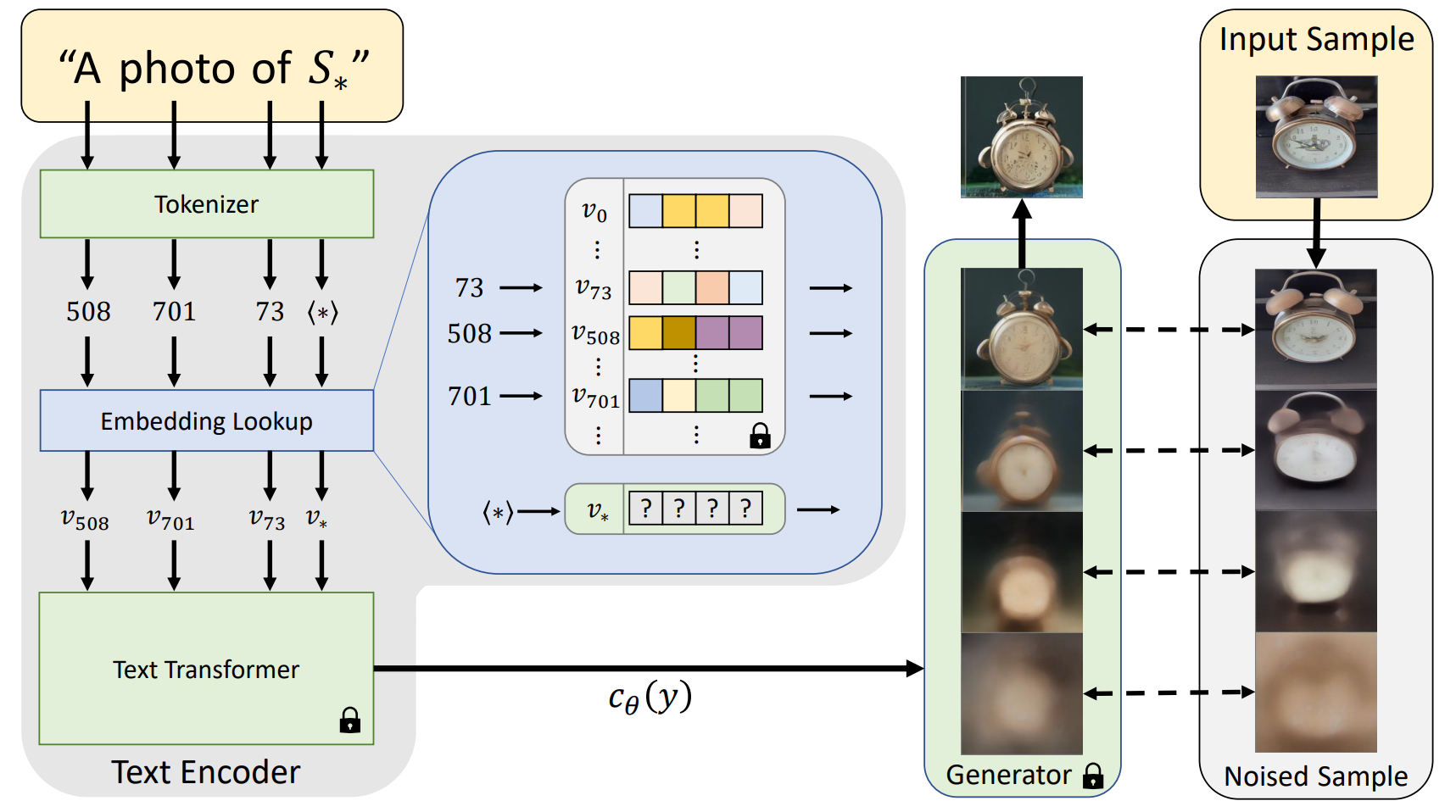
适配器 / LoRA-s
开源扩散模型通常使用全微调或适配器(如 LoRA-s)进行微调。这需要更多的 GPU 内存、训练数据和时间来训练,但质量也更高。
如前所述,可以通过多种方式融合这些适配器或文本反演。这些 LoRA-s 可以通过取它们的加权平均值或通过在从各个 LoRA-s 提取的特征上训练融合的 LoRA 来组合。
$W = \sum\limits_{i=1}^n w_i W_i$
$W = argmin_W \sum\limits_{i=1}^n ||(W_0 + \Delta W_i) X_i - W X_i||_F^2$

潜在一致性
引入了 LDMs 的另一个加速方法,即潜在一致性模型。与在反向过程中预测 $\epsilon_\theta$ 不同,LCMs 直接训练 $f_\theta$ 估计器来预测 $x_0$。作为一种自蒸馏任务,我们可以运行长生成序列的反向过程,然后使用较低阶时间步长的 $x_0$ 预测作为目标。
其中 $\theta’$ 是一组扩展参数,$\psi$ 是一个求解器,如 DDIM,$w$ 是引导权重,$d$ 是距离函数,$\tau$ 是一组解码时间步长。
DALL-E 3 使用这种方法实现 $2-4$ 步生成。
潜在一致性结果

潜在一致性 LoRA
上述训练目标也适用于 LoRA 训练。此 LoRA 模型可用作多个 LDM 的加速器,原始 LDM 的适配器也可与此 LCM-LoRA 一起使用。

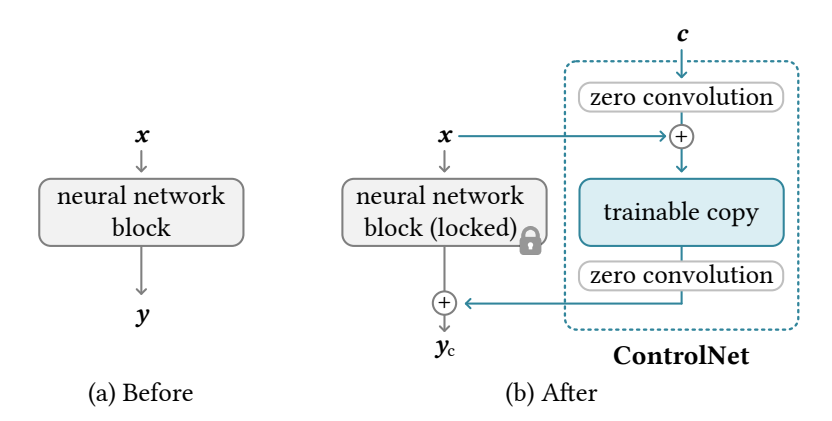
ControlNet
控制 LDM 的条件注入很难,添加额外的控制模态需要重新训练。ControlNet 系列创建了一组适应方法,可用于在不重新训练的情况下控制文本到图像模型。
原始 ControlNet 是 SD UNet 编码器的完整并行副本,经过训练以引导原始模型在额外的模态(如分割掩码、姿势、涂鸦等)上进行操作。
文本到图像适配器和 LoRA 也可用于在不重新训练的情况下实现控制。
这些方法可以在推理时相互混合使用。
T2I 适配器
ControlNet 结果

NLP-TextImageModels