NLP-StaticNeuralEmbeddings

静态嵌入式神经网络

词向量和神经网络

LSI 和 LSA 的成功表明，基于分布的词向量表示对于 NLP 任务非常有用。在神经网络 NLP 模型中，连续的、密集的词表示尤其重要，因为它们

• 可以用作信息丰富且经济的表示，而不是简单地对词进行独热编码
• 可以帮助减少模型参数的数量
• 可以通过神经网络从文本语料库中以自监督的方式学习

一个由神经网络学习到的词向量的最早实例之一可以在语言模型中找到：

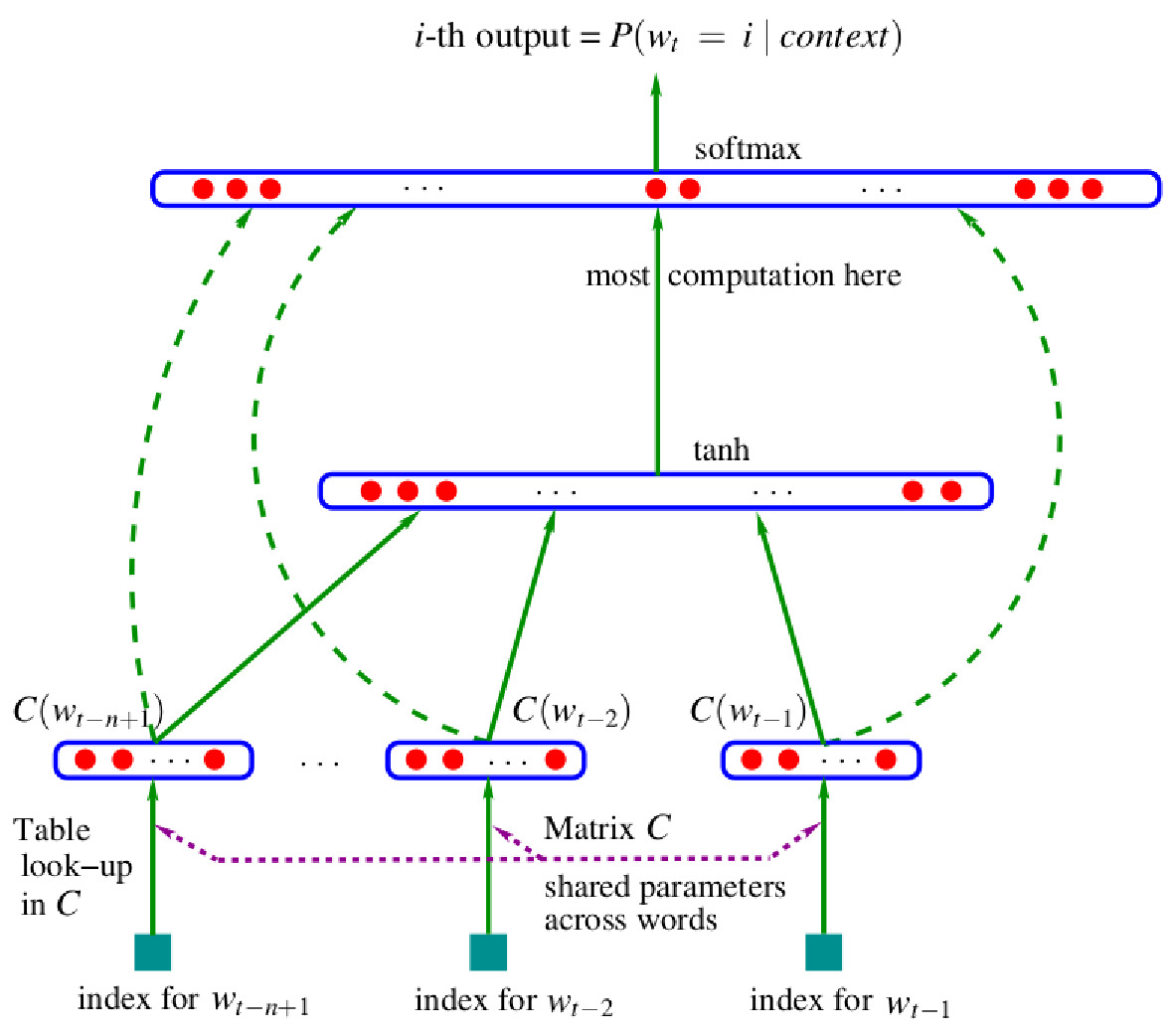
$C$ 是一个嵌入层，将词汇索引映射到实数向量：

$$C: [0, |V|-1] \rightarrow \mathbb R^d$$

（静态）词嵌入的维度通常在 50 到 600 之间。

从技术上讲，嵌入层可以通过多种方式实现，例如，作为一个以独热编码词索引为输入的密集层（在这种情况下，词向量表示为层的权重矩阵），或者作为一个表示为数组的查找表等。

关于嵌入层的重要经验教训：

• 嵌入是静态的：相同类型的标记在不同上下文中具有相同的嵌入
• 使用端到端训练的词嵌入层的模型比传统的 n-gram 语言模型表现更好
• 使用词共现频率矩阵的前几个主成分作为词特征向量，而不是训练的嵌入，没有同样的性能优势
• 使用神经网络学习词嵌入是一种扩展训练语料库的可行方法

Word2vec

区别特征

Word2vec，也是一个神经网络家族，从语料库中学习有用的分布式词表示，但具有几个新颖的特征：

• 它是一个专用架构：表示学习 （representation learning）是其唯一目标

• 它基于一种新的基于语料库的自监督预测任务

• 架构被故意保持非常简单，以便能够在具有大词汇量的巨大语料库上进行训练

Skipgrams

Word2vec 基于 skipgrams，它是 $n$-grams 的推广：虽然 $n$-gram 是文本的连续、长度为 $n$ 的子序列，但 skipgrams 可以包含一定数量的“jumps”：如果基本序列是 $\langle w_1, \dots ,w_N \rangle$，那么具有最多 $k$ 跳距的 $n$ 长度 skipgrams 集合是

$$
{\langle w_{i_1} ,\dots ,w_{i_n}\rangle | i_1<\dots<i_n\in[1, N],i_n - i_1 \leq n -1 + k }
$$

可以有额外的限制，例如对单个跳跃的数量和长度的限制。

Word2vec 任务

Word2vec 任务具体基于长度为 $2c$ 的 skipgrams，在中心有一个单词跳跃。有两种任务变体及其相关的模型架构：

• CBOW: Continuous Bag of Words 预测 skipgram 中心的缺失词
• SkipGram: 给定 缺失/跳过 的词，预测 skipgram 的元素。与 CBOW 任务不同，每个 skipgram 对应一个分类示例，SkipGram 任务为每个 skipgram 生成多个 $\langle$ 中心词，skipgram 中的词 $\rangle$ 示例

skipgram 任务的简单示例：

架构

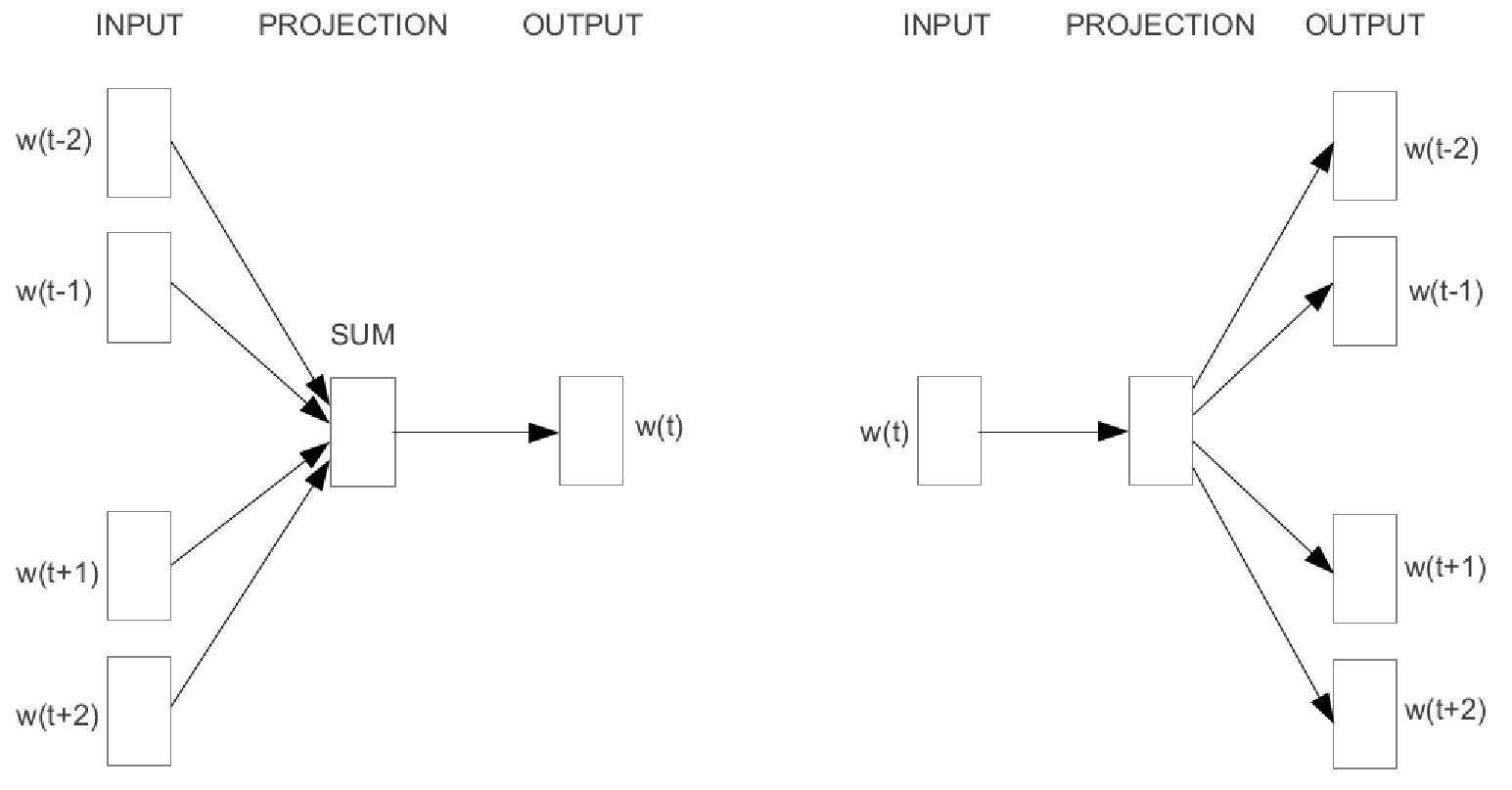
虽然 SkipGram（右）只是将 $E(\cdot)$ 嵌入映射应用于其一个词输入，CBOW（左）嵌入输入 skipgram 中的所有词并计算它们的和。

在将输入投影到词嵌入空间后，这两种架构都仅使用一个带权重矩阵 $W \in \mathbb R^{|V|\times d}$ 的线性投影和一个最终的 softmax 层来生成词汇表中所有词的预测概率：

$$CBOW(\langle w_{t-c},\dots ,w_{t+c} \rangle) = \mathop{\mathrm{softmax}}(W\sum_{i}E(w_i))$$

$$SkipGram(w_t) = \mathop{\mathrm{softmax}}(W_{}E(w_t))$$

这两种模型都使用标准的负对数似然损失和 SGD 进行训练，但在示例采样方面有一些有趣的差异。

值得注意的是，投影矩阵 $W \in \mathbb R^{|V|\times d}$ 也可以看作是词汇表在相同 $R^d$ 空间中的 $E’(\cdot)$ 嵌入。使用这种表示法，两个模型对于特定单词 $w_j$ 的 logits（线性输出）可以简单地写成：

$$CBOW_{linear}[\langle w_{t-c}, \dots ,w_{t+c} \rangle](w_j) = \sum_{i}E(w_i) \cdot E'(w_j),$$

$$SkipGram_{linear}[w_t](w_j) = E(w_t) \cdot E'(w_j)$$

如这种表示法所示，最小化负对数似然训练目标是一种增加输入嵌入和正确预测嵌入的点积的方法。

由于这种表示法所显示的对称性，可以选择绑定两层的权重，使得对所有 $w\in V$ 都有 $E(w) = E’(w)$。

尽管这种方法经常被采用，但通常也会保持它们的不同，并且仅使用输入嵌入 $E(\cdot)$ 的向量作为最终结果，或者将它们结合起来，例如取它们的平均值。

数据点生成和采样

对于 CBOW 变体，我们只需将 $c$ 半径的上下文窗口滑动通过语料库，并在每一步生成一个

$$\langle \langle w_{t-c}, \dots ,w_{t-1}, w_{t+1}, \dots ,w_{t+c} \rangle, w_t \rangle$$

$\langle$ 输入，正确输出 $\rangle$ 数据点。

对于 SkipGram，过程更为复杂，因为在每一步中，实际使用的上下文窗口半径 $r$ 是从 $[1, c]$ 区间内随机选择的，并且为每个 $w_i\in \langle w_{t-r}, \dots ,w_{t-1}, w_{t+1}, \dots ,w_{t+r}\rangle$
单词生成一个 $\langle w_t, w_i\rangle$ 数据点。其效果是离目标词越近的词被采样的概率越高。

避免 full softmax

由于对一个 $|V|$ 长度的向量计算全 softmax 对于大 $V$ 来说是昂贵的，Word2vec 实现通常使用更便宜的输出层替代方案。

一种解决方案是 hierarchical softmax，它基于一个二叉树，其叶子是词汇表中的单词。网络的线性输出对应于内部节点，分配给一个单词 $w$ 的概率可以通过仅计算路径上 $o$ 输出的 $\sigma(o)$ 值来计算。使用平衡树，这个技巧将训练期间 softmax 计算的复杂度从 $\mathcal O(|V|)$ 降低到 $\mathcal O({\log |V|})$，并且通过巧妙的树结构可以进一步减少。

Hierarchical softmax

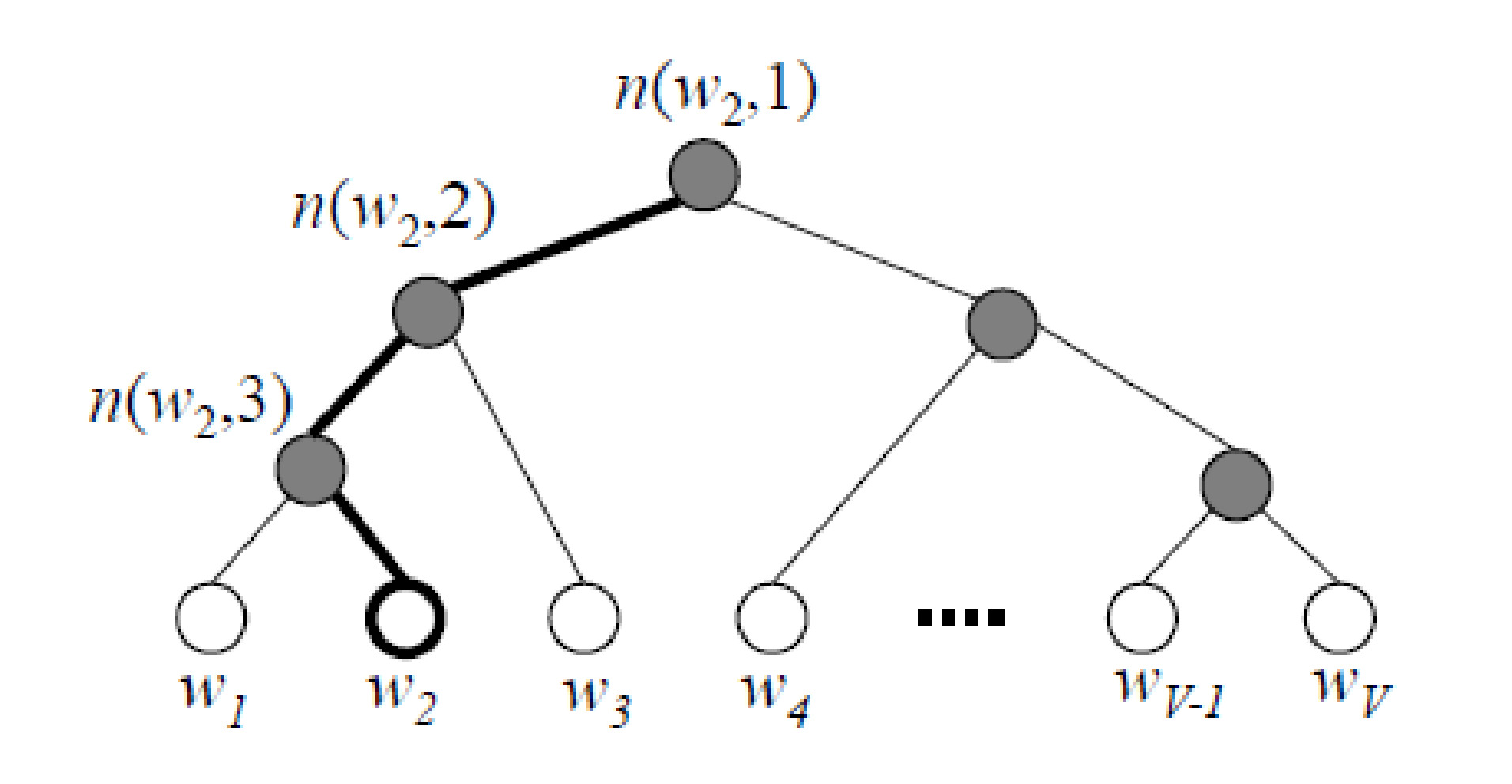
说明：如果路径上的线性输出是 $o(w_2, 1), o(w_2, 2), o(w_2, 3)$，那么分配给 $w_2$ 的概率可以计算为 $(1-\sigma(o(w_2,1)))(1-\sigma(o(w_2,2)))\sigma(o(w_2,3))= \sigma(-o(w_2,1))\sigma(-o(w_2,2))\sigma(o(w_2,3))$。

负采样

另一种替代方案是 Negative sampling。这涉及将 SkipGram 任务重新表述为一个二元分类问题。

• 我们将语料库中的早期 SkipGram $\langle$ 中心词，背景词 $\rangle$ 数据点视为正例

• 并且通过从代表整个语料库的噪声分布中采样，为每个中心词生成一定数量的负例“假背景词”

负采样技巧使得简化网络架构成为可能，达到

$$SGNS(w_{t}, w_{c}) = \sigma(E_t(w_t)\cdot E_c(w_c))$$

其中 $E_t(\cdot)$ 是目标（中心）词嵌入，而 $E_c(\cdot)$ 是背景词嵌入。对于从 $P_n$ 噪声分布中采样的 $k$ 个负样本，每个真实 $\langle w_t, w_c\rangle$ 数据点的负对数似然损失将是

$$- [ \log SGNS(w_{t}, w_{c}) + \sum_{\substack{i=1 \ w_i \sim P_n}}^k \log(1 - SGNS(w_{t}, {w_i}))]$$

Word2vec 作为矩阵分解

在 Word2Vec 成功之后，许多研究调查了它与基于计数的矩阵分解方法的关系，结果发现它们密切相关：SGNS 目标等价于分解基于词共现的 $M$ 矩阵，其元素为

$$m_{ij} = \max(0, PMI(w_i, w_j )- \log k)$$

其中 $PMI(w_i,w_j)$ 是 $w_i$ 和 $w_j$ 的 $\log\left(\frac{P(w_i, w_j)}{P(w_i)P(w_j)}\right)$ 点互信息，$k$ 是负样本的数量。

Pointwise Mutual Information

PMI 衡量单词在彼此上下文中出现的频率与它们独立出现的频率相比的差异。上下界由 $w_i$ 和 $w_j$ 从不 ($P(w_i, w_j) = 0$) 或总是 ($P(w_i, w_j) = P(w_i)$ 或 $P(w_i, w_j) = P(w_j)$) 共现的情况提供：

$$-\infty \leq PMI(w_i, w_j) \leq \min(-\log(p(w_i)), -\log(p(w_j)))$$

PMI 公式中的 $\frac{P(w_i, w_j)}{P(w_i)P(w_j)}$ 比例可以基于目标词-上下文词共现计数估计为

$$\frac{C(w_i, w_j)C(\mathrm{\langle target~word, context~word\rangle~pairs~in~corpus})}{C(w_i)C(w_j)}$$

在一个大型维基百科片段中，PMI 分数最高和最低的三组二元组：

单词 1	单词 2	PMI
puerto	rico	10.03
hong	kong	9.72
los	angeles	9.56
$\cdots$	$\cdots$	$\cdots$
to	and	-3.08
to	in	-3.12
of	and	-3.70

GloVe

GloVe [Global Vectors] 是另一种从非常大的语料库中学习静态词嵌入的算法。它不是一种神经方法，但在这里讨论是因为它在 Word2vec 之后（一年）发表，作为对其的反应，并且是其最重要的替代方案之一。

与 LSA 方法类似，GloVe 明确基于固定大小上下文窗口中词共现的矩阵的低秩分解，但矩阵元素实际上是词共现的对数。

关注共现的对数是基于以下观察的动机：共现概率的比率在语义上非常有信息量：

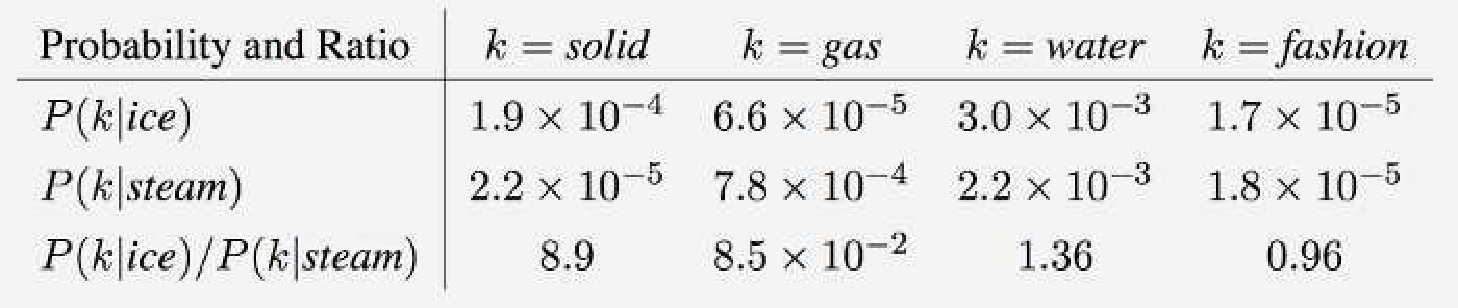
该表显示了比率在区分与词对冰、蒸汽相关的词（即固体和气体）与噪声词方面做得很好。

直接分解共现对数概率矩阵需要对于任何 $w_i$, $w_j$ 词对满足

$$ E_w(w_i)\cdot E_c(w_j)\approx \log (P(w_j~|~ w_i)) \approx \log (C(w_i, w_j)) - \log (C(w_i)) $$

其中 $E_w(\cdot)$ 词嵌入和 $E_c(\cdot)$ 上下文嵌入满足这个要求，$\log(P(w_k \space | \space w_i)/P(w_k \space | \space w_j))$ 对数概率比可以简单地表示为 $(E_w(w_i) - E_w(w_j))\cdot E_c(w_k)$，即语义上信息丰富的共现关系对应于嵌入之间的简单几何关系。

GloVe 不尝试最小化 $E_w(w_i) \cdot E_c(w_j) + \log (C(w_i)) - \log (C(w_i, w_j))$ 的差异对于 $w_1,w_2\in V$，而是最小化密切相关的

$$\sum\limits_{i, j=1}^{|V|} f(C(w_i,w_j)) (E_w(w_i)\cdot E_c({w}_j) + b_w(w_i) +
{b_c}(w_j) - \text{log} C(w_i, w_j))^2$$

目标。差异在于

• $f(\cdot)$ 加权函数对稀有共现进行降权，
• 为每个词学习的 $b_w$ 和 $b_c$ 偏差，提供了 $\log(C(w_i))$ 的对称替代。

GloVe 训练

与通过滑动上下文窗口训练的 Word2vec 不同，GloVe 的训练分为两个步骤：

1. 组装全局共现计数矩阵

2. 通过随机梯度下降（SGD）优化上述目标中的 $E_w, E_c, b_w, b_c$ 参数，随机采样共现矩阵的元素

与 Word2vec 相比，GloVe 由于处理共现矩阵（尽管是稀疏的）可能需要更大的内存，但这可以通过在之后对非零矩阵元素进行优化来补偿，其数量通常在语料库长度上是次线性的。

评估

评估类型

如何衡量词嵌入的质量？作为学习到的表示，词向量可以通过以下方式进行评估：

• 内在地，intrinsically 根据它们与人类对词语语义和形态特征的判断的对应程度

• 外在地，extrinsically 根据它们在下游 NLP 任务解决方案中的有用程度

从内在的角度来看，使用适当调整参数并在大型高质量语料库上训练的 Word2vec 可以生成几何特性与人类相似性判断惊人接近的嵌入。

内在评估

评估词嵌入质量的两种最常用的内在方法是测试它们在两个词汇语义任务中与人类判断的相关性：

1. 词相似度 Word similarity

2. 类比 Analogy

相似度

相似的词应该有相似的向量。

• 语义：dog - hound

• 语法：dogs - pears

两个词的相似度通过它们表示的余弦相似度来衡量：$\frac{E(w_1)\cdot E(w_2)}{|E(w_1)|\times |E(w_2)|}$。

注意：归一化很重要，因为向量的长度大致与词频的对数成正比。

相似度可以通过使用降维技术（例如 t-SNE 或 UMAP）进行可视化，例如：

类比

Analogy 任务测试词之间的 关系，例如 $king:queen$ 和 $man:woman$，它们在向量空间中的几何关系是否相似。

这些关系对应于向量的差异，即 $E(king)-E(queen)\approx E(man)-E(woman)$

或者，以稍微不同的形式，嵌入最接近 $E(king)-E(queen) + E(woman)$ 的词是否是 $man$。

语义和句法类比的示例：

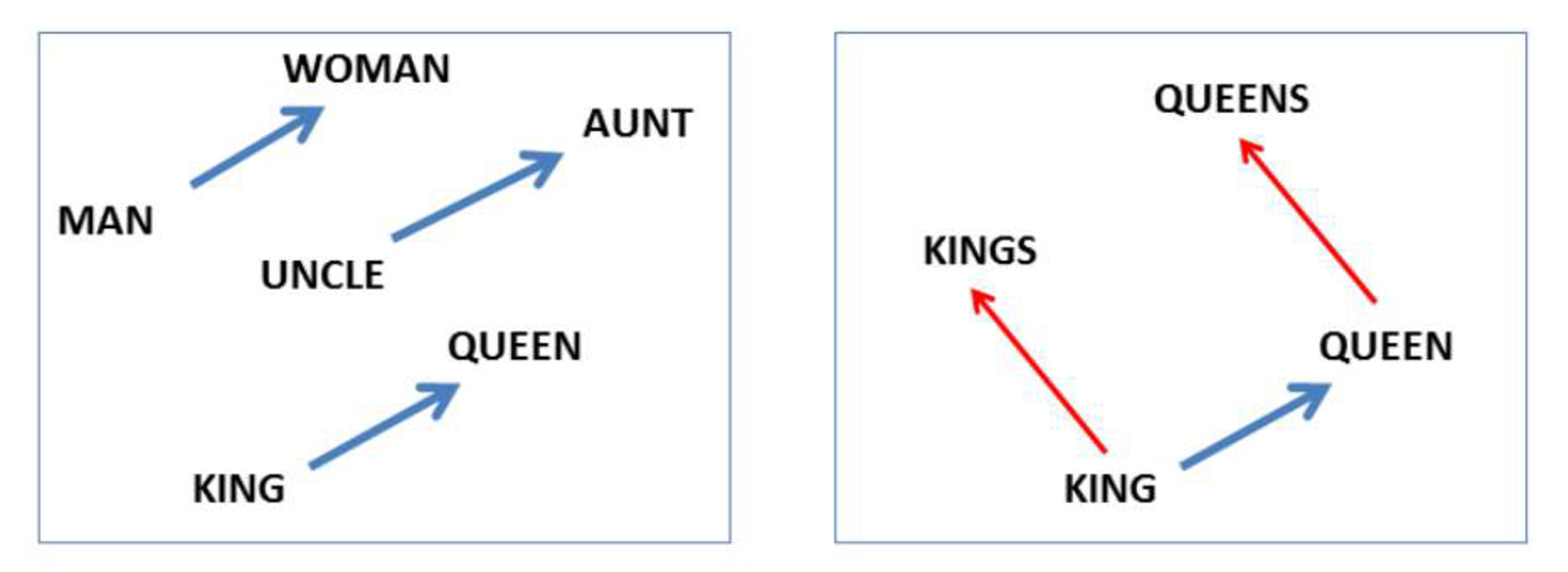
数据集

也有一些专门用于内在评估的数据集，例如：

• WordSim-353 数据集包含 353 对英语单词及其语义相似度分数，范围从 0.0 到 10.0。（注意：原始数据集混淆了相似性和相关性；链接版本大多修正了这一点。）

• SimLex-999 取代了 WordSim-353，包含 999 对单词及其相似度分数，使用相同的评分尺度。

• BATS（The Bigger Analogy Test Set）包含 98000 个类比问题，用于测试单词类比与向量偏移之间的对应关系。

外在评估

Extrinsic 评估可以使用任何 NLP 任务进行，但通常使用标准的序列标注任务，例如命名实体识别。

可以通过在嵌入式架构中切换不同的嵌入来评估它们，同时保持其他部分不变。

在使用嵌入时，有一个重要的区别是直接使用嵌入（“冻结”）而不改变它们，还是对它们进行 微调，即在任务数据集上与其他参数一起训练它们。

评估结果

在某些共现矩阵上，Word2vec 变体、GloVe 和传统 SVD 之间的性能差异不大。最重要的是，他们发现

• 超参数调优对性能的影响大于算法的选择

• SGNS 被证明是一个非常强的基线，在任何情况下都没有“显著表现不佳”

• 两个学习到的嵌入（目标和上下文）的和通常比单独使用其中一个表现显著更好

利用内部词结构

Utilizing internal word structure

黑箱问题

我们讨论的词嵌入完全基于分布，词的内部结构不起作用。因此，

• 词汇表外的词，和
• 在训练语料库中罕见的词

没有足够的嵌入，即使它们的 内部形态/字符结构（internal
morphological/character structure） 可以提供关于其语义和句法属性的丰富信息。

除了使用需要形态分析器的词素（morpheme）嵌入外，还出现了一些自监督解决方案。

fastText

fastText 算法基于 SGNS，但将 $n$-grams ($3\leq n \leq 6$) 添加到词汇表中，并将目标词建模为其所有组成部分嵌入的总和。

例如，对于单词 where 和 $n=3$，其组成部分是 <wh、whe、her、ere、re>，加上整个单词 <where>。

SGNS 架构被修改为

$$\sigma(\sum_{w\in G(w_t)}E_t(w)\cdot E_c(w_c))$$

其中 $G(w_t)$ 是 $w_t$ 的所有组成部分的集合。

在相似性任务中，fastText 向量通常比原始 Word2vec 表现更好，尤其是在形态丰富的语言中。

一个额外的重要优势是，使用 fastText 可以通过将其组成 $n$-grams 的嵌入相加来生成未见词的有信息嵌入。

子词嵌入

解决黑箱问题的一个更激进的解决方案是切换到子词分词（例如，使用 BPE）并使用已建立的算法仅为词汇表中的子词生成嵌入。

例如，PBEmb 使用 GloVe 为 BPE 分词生成的子词生成嵌入。类似于 fastText，可以通过组合组成子词的嵌入（例如，取平均值）来生成 OOV 词的嵌入。虽然表现相似，但这种类型的解决方案所需的词汇表明显小于 fastText。