NLP-Seq2Seq
RNN 序列模型和注意力
基于 RNN 的序列处理
根据输入、输出和 hidden/cell 状态的处理方式,RNN 可用于各种序列转换和处理任务:
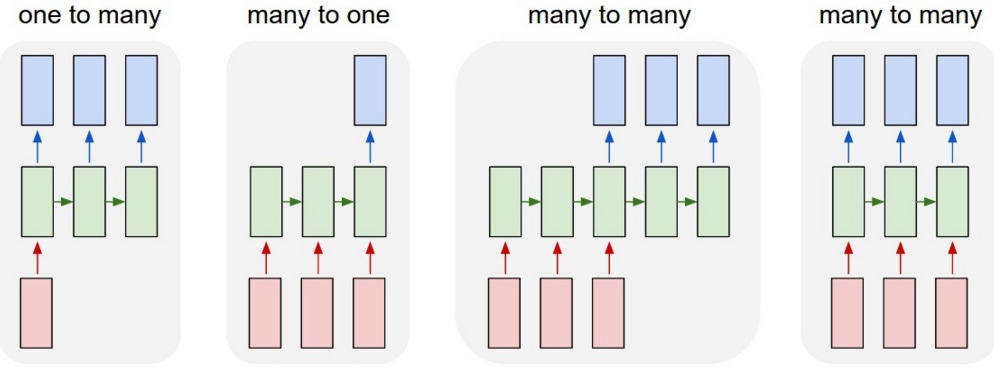
也许最基本的是将 $\langle \mathbf{x}_1,\dots,\mathbf{x}_n \rangle$ 输入序列转换为 $\langle \mathbf{y}_1,\dots,\mathbf{y}_n\rangle$ 序列的对应输出。
这种类型的架构可以用于序列标注,当输出是标签的分布时。例如,语言建模可以被视为序列标注的一个特例,当文本中每个单词的正确“标签”只是下一个单词:
$$\mathbf{x} = \langle w_1,\dots,w_{n-1}\rangle$$
$$\mathbf{y} = \langle w_2,\dots,w_{n}\rangle$$
序列标注
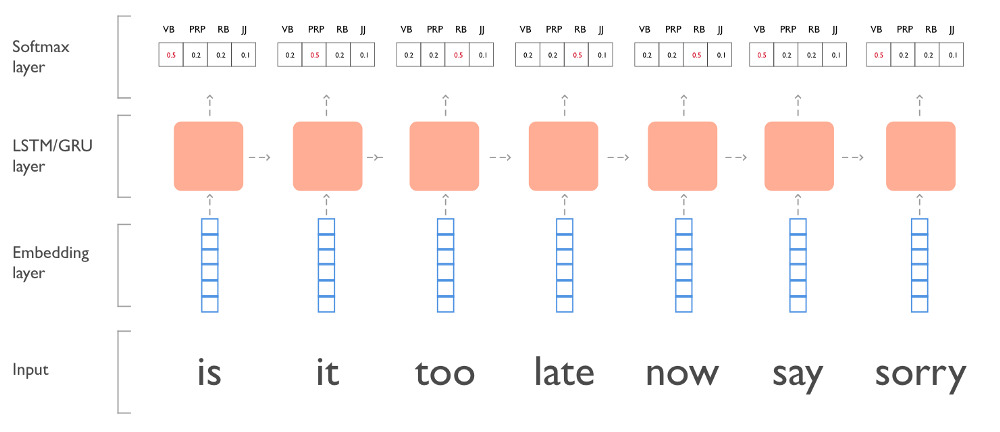
一个简单的标注示例:基于 LSTM 的词性标注器,具有词嵌入输入和 softmax 输出层。
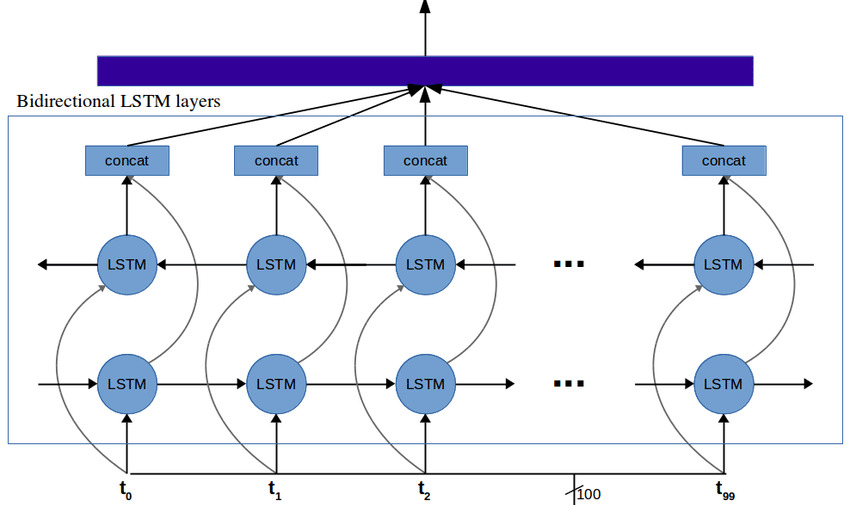
双向 RNN
作为序列标注任务的语言建模有一个非常特殊的属性:模型不能访问要标注元素之后的元素信息。
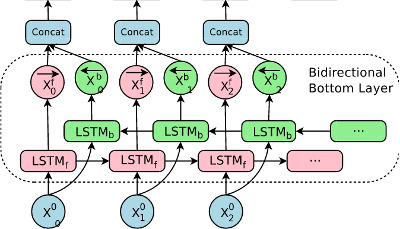
对于其他序列标注任务,这种情况并不成立:元素之后的上下文是输入的重要组成部分。但 RNN 单元本质上是单向的:隐藏状态只能包含关于较早时间步输入的信息。一种广泛使用的方法是使用双向 RNN 并在每个元素处连接它们的隐藏状态。这就是所谓的 Bidirectional RNN 层。
自然地,双向 RNN 层可以像普通的单向 RNN 一样堆叠:
Seq2vec: 序列编码
有许多任务需要将可变长度的输入序列映射到固定长度的输出,例如情感分类等序列分类任务。
如何使用一个或多个堆叠的 RNN 将输入序列映射到一个有用的表示整个输入的向量?关键在于 RNN 的 隐藏状态(加上 LSTM 的 cell 状态)可以表示到给定时间步的整个输入序列。
对于单向 RNN,显而易见的解决方案是使用最后的隐藏状态(在 LSTM 的情况下可能还包括 cell 状态)来表示整个输入序列。例如,对于分类任务:
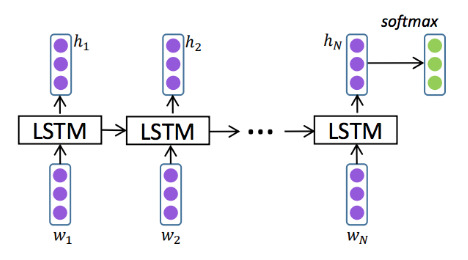
相比之下,双向 RNN 的隐藏状态在每个时间步都包含关于整个输入的信息,因此更有意义的是聚合所有隐藏状态,例如,使用平均或最大池化。
Vec2seq: 序列生成
基于固定大小向量的序列生成类似于使用语言模型的语言生成,但在这种情况下,生成是有条件的:我们希望建模序列概率
其中 $\mathbf{x}$ 是一个固定长度的向量。类似于基于 RNN 的无条件语言模型,我们可以将问题简化为使用 RNN 建模个体
$$P( y_n|~ \langle y_1,\dots,y_{n-1} \rangle, \mathbf{x})$$
续接概率。
标准的基于 RNN 的语言模型架构可以通过一个简单的修改来重用:RNN 的隐藏状态也依赖于条件向量 $\mathbf{x}$。模型具有以下条件独立结构:
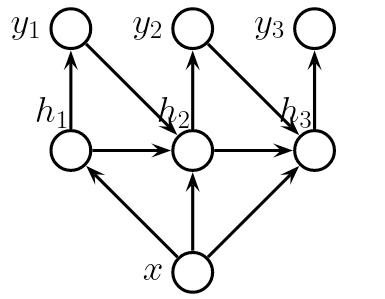
在神经网络架构层面,可以通过多种方式将 RNN 的隐藏状态依赖于 $\mathbf{x}$:
- 使用 $\mathbf{x}$(直接或经过转换)作为 RNN 的初始隐藏状态(对于 LSTM 也作为初始 cell 状态)
- 使用 $\mathbf{x}$(直接或转换后)作为第一个时间步的输入
- 使用 $\mathbf{x}$(直接或转换后)作为每个时间步的输入(除了已经生成的序列元素之外)
最常用的两种解决方案,例如,以下图像字幕模型使用图像的特征向量作为第一个 LSTM 输入:
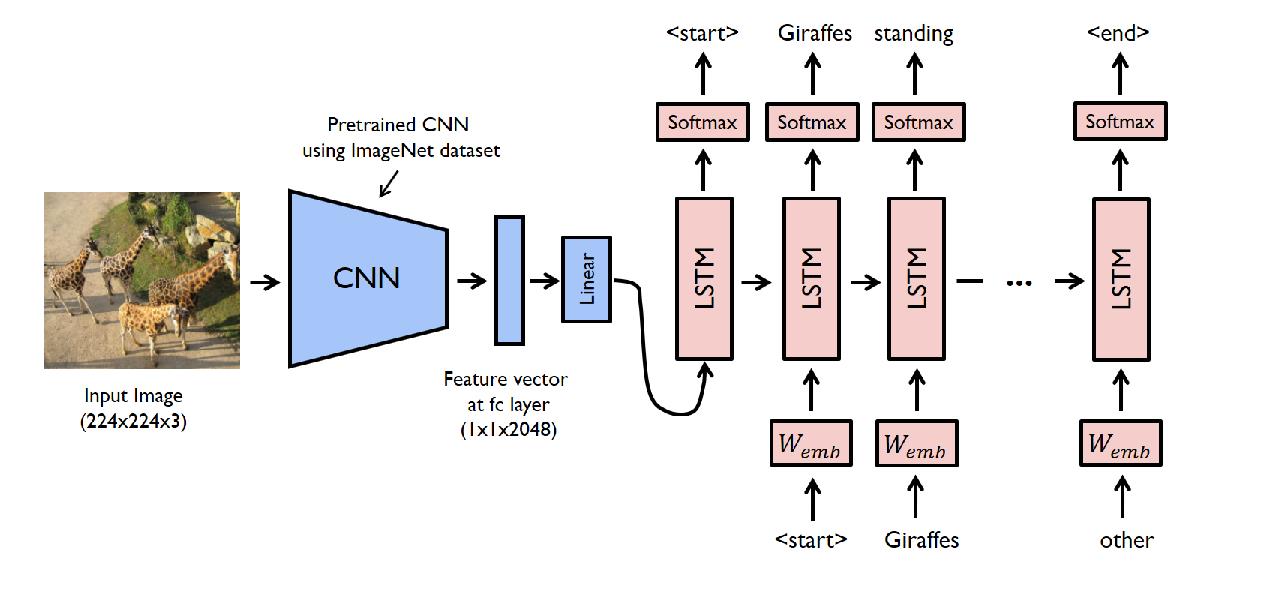
Vec2seq 模型的训练同样类似于无条件语言模型的训练:
主流策略是 教师强制:训练数据集的序列用作 RNN 输入,预测的续接概率仅用于计算损失(负对数似然)。
与无条件情况一样,教师强制会导致 暴露偏差(训练和推理设置之间的不健康差距),因此也使用诸如计划采样等替代训练策略。
基于 RNN 的 Seq2seq
通过将 RNN Seq2vec 与 RNN Vec2seq 模块结合,我们可以构建一个 Seq2seq 模型,该模型通过首先将输入编码为固定大小的向量表示,然后将该向量解码为另一个序列,从而将可变长度的输入序列转换为另一个未对齐(unaligned)的序列。组合模型的概率结构如下:
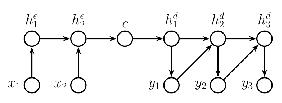
历史上,基于 RNN 的 Seq2seq 模型是 RNN(更具体地说,是 LSTM 变体)最成功的应用之一。应用包括:
- 机器翻译(LSTM Seq2seq 模型是第一个与传统短语翻译解决方案竞争并后来优于它们的神经机器翻译模型)
- 摘要生成
- 问答系统
- 对话系统
在架构上,这些模型通常是:
- 基于嵌入的
- 在编码器和解码器中使用多个 LSTM 层
- 使用编码器的(最后或聚合的)隐藏状态和 cell 状态初始化解码器的隐藏状态和 cell 状态
- 像往常一样,通过教师强制和负对数似然损失进行训练
虽然解码器不能包含反向 RNN(显而易见的原因),但编码器通常包含双向 RNN 层。
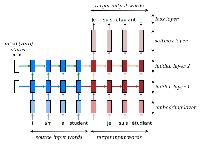
这个模型展示了如何将一个输入序列翻译成另一个语言的输出序列。编码器将输入序列编码成一个固定长度的向量,解码器则根据这个向量生成目标语言的序列。该模型通常使用注意力机制来提高翻译质量。
注意力机制
在基本的 RNN Seq2seq 模型中,如我们所见,解码器只能以编码器生成的固定大小向量表示形式访问编码的输入序列。
显著的是,这个固定大小的“摘要”并不依赖于解码器在解码过程中的位置,尽管我们知道对于典型的 Seq2seq 任务,例如翻译,输入的不同部分在不同的解码阶段是相关的。
即使固定大小的向量是通过对整个编码器隐藏状态序列进行池化生成的,解码器的上下文对池化没有影响。
注意力机制通过在每个解码时间步提供对编码器隐藏状态的动态池化版本的访问来解决这个问题,基于编码器的上下文,即 $h_{t-1}^d$ 隐藏状态:
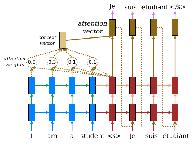
具体来说,注意力机制基于 $h^d_{t-1}$ 解码器上下文使用 $s(\cdot, \cdot)$ 评分函数对 $\mathbf{h}^e=\langle h_1^e\dots,h_n^e \rangle$ 编码器隐藏状态进行评分,并使用得分的 softmax 产生加权和:
$$\mathbf{s}(\mathbf{h}^e, h_{t-1}^d ) =\langle s({h}^e_1, h_{t-1}^d),\dots, s({h}^e_n, h_{t-1}^d) \rangle$$
$$\mathcal A(\mathbf{h}^e, h_{t-1}^d) = \mathop{\mathrm{softmax}}(\mathbf{s}(\mathbf{h}^e, h_{t-1}^d )) \cdot \mathbf{h}^e$$
注意力机制:评分函数
根据评分函数的类型,注意力机制主要有两种类型:
加性 或 MLP 或 Bahdanau 注意力:评分通过一个简单的具有一个隐藏层的前馈网络计算:
$$s_{add}(\mathbf{a}, \mathbf{b}) = \mathbf{v^\intercal}\tanh(\mathbf{W_1\mathbf{a} + \mathbf{W_2} \mathbf{b}})$$
其中 $\mathbf{v}$、$\mathbf{W}_1$ 和 $\mathbf{W}_2$ 是学习到的参数。
乘性 或 Luong 注意力:评分计算为
$$s_{mult}(\mathbf{a}, \mathbf{b}) = \mathbf{a}^{\intercal} \mathbf{W} \mathbf{b}$$
其中 $\mathbf{W}$ 同样是学习到的参数。
点积注意力
Dot product 评分是一种重要的、简单的乘性评分变体,其中 $\mathbf{W}$ 是单位矩阵,即,
$$s_{dot}(\mathbf{a}, \mathbf{b}) = \frac{\mathbf{a} \cdot \mathbf{b}}{\sqrt d}$$
其中 $d$ 是 $\mathbf{a}$ 和 $\mathbf{b}$ 的维度,除以 $\sqrt d$ 确保如果 $\mathbf{a}$ 和 $\mathbf{b}$ 输入具有 0 均值和 1 方差,则得分也具有 0 均值和 1 方差。
注意力机制带来的性能提升
将注意力机制添加到 RNN Seq2seq 架构通常会带来显著的性能提升,在翻译任务中困惑度降低了 11%,BLEU 分数提高了 20%。
因此,最先进的 RNN Seq2seq 模型几乎总是包含某种类型的注意力机制。
注意力权重可视化显示了它们如何反映对解码步骤的相关性:
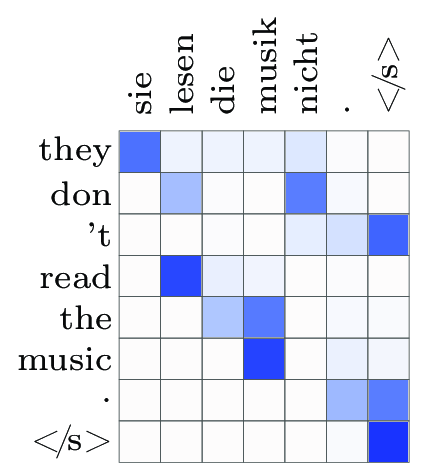
前言:卷积神经网络(CNNs)
尽管我们的讨论集中在 RNN 上,但卷积网络在许多 NLP 任务中也相当有竞争力。它们使用一维卷积:

…以及一维(通常是最大或平均)池化层。事实上,表现出色的 fastText 分类模型使用了没有卷积的池化:
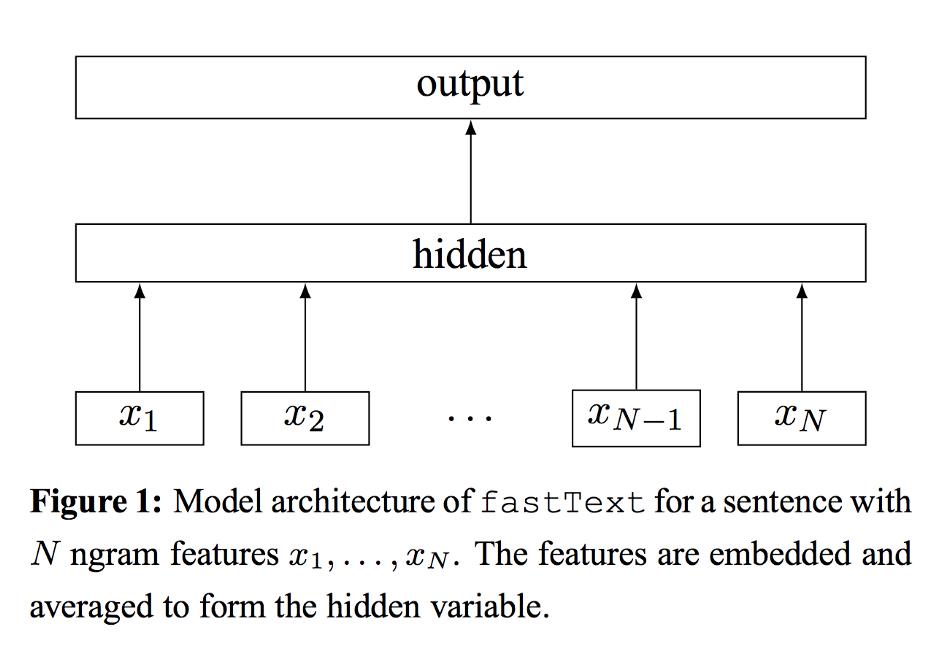
NLP-Seq2Seq