NLP-ReducedComplexity

精简

介绍

从第一天开始，LLM 的参数数量就一直在增加，即使在神经 LMs 的扩展规律确立之前也是如此。如前所述，大型模型存在各种问题：

• 不利的环境影响
• 非常高的硬件要求
  • 推理
  • 微调

在今天的讲座中，我们将看到一些可能缓解这些问题的方法。

这些“规律”不是严格的数学构造，更像是摩尔定律。

蒸馏

知识 distillation

LMs（或任何分类模型）通常通过最小化模型预测与独热训练标签之间的交叉熵来进行训练。

这种设置忽略了单词之间的关系（例如同义词）。例如，模型最终会学到汽车、火车和卡车都是车辆，但在任何训练句子中，只有一个是正确的，并且只有它的概率会增加。这会减慢训练速度。

知识蒸馏使用较大模型（教师）的输出来替换训练较小模型（通常是学生）时的独热标签。

学生通过蒸馏损失进行训练：即与教师的（软）目标分布的交叉熵：

$$L_{ce} = \sum_i t_i * log(s_i)$$

还使用了参数化的 softmax 版本

$$p_i = \frac{\exp{(z_i / T)}}{\sum_j \exp{(z_j/T)}}$$

其中 $T$ 是控制分布平滑度的温度。在训练期间，使用 $T>1$ 的值来放大教师知识中的隐含 implicit 泛化 generalization。

DistilBERT

DistilBERT 将 BERT-base 蒸馏为一个层数减半的模型。训练损失有三个组成部分：

• 蒸馏损失 $L_{ce}$
• 掩码语言模型 损失 $L_{mlm}$
• 余弦嵌入损失 $L_{cos}$ 用于对齐隐藏向量

小模型保留了 BERT 在 GLUE 上 $97%$ 的性能，同时体积减少了 $40%$，推理时间加快了 $60%$。

蒸馏主要用于预训练，但在一个任务中，微调后的模型也通过蒸馏进行训练。

Switch Transformer

Switch Transformer 是一个拥有 1.6T 参数的 LLM。该模型使用 专家混合 设置来实现稀疏性：

• Hard 专家切换：一次只激活一个专家
• MoE 仅应用于 FF 层
• 预训练速度提高 $7\times$

该模型非常强大，但太大而无法有效使用。使用与 DistilBERT 相同的技术：

• 从教师模型初始化学生权重
• 硬损失和软（教师）损失的 $75$–$25%$ 混合

蒸馏后的 密集 dense 模型（压缩率为 $80-99%$）仍保留了教师模型质量提升的约 $30%$。

量化

量化 是将连续值映射到一小组离散 discrete 值的过程。
除了蒸馏，它是另一种减少 LLM 内存使用的方法，使得在单个 GPU 上运行大型模型成为可能。

形式上，量化的目标是给定（层）权重矩阵 $\mathbf{W}$ 和层输入 $\mathbf{X}$，找到量化后的权重矩阵 $\mathbf{\hat{W}}$ 使得

$$\mathbf{\hat{W}} = \textrm{argmin}_\mathbf{W_q} |\mathbf{WX} - \mathbf{W_qX}|_2^2$$

量化 LLMs

量化 LLMs 并不是一项简单的任务：

• 最简单的四舍五入到最接近（round-to-nearest）方法仅在 8 位/权重时效果良好
• 需要模型再训练的高级方法在 GPT-3 级别的模型（如 OPT-175B 或 BLOOM）上非常昂贵
• 训练后（一次性）方法复杂且在大约 15 亿参数时变得不可行

引入了 GPTQ / OPTQ 算法，这是第一个可以将 OPT 或 BLOOM 量化到 3-4 位的算法。

算法

该算法是Optimal Brain Quantization算法的增强版本。OBQ 逐行逐个权重地量化 $\mathbf{W}$，始终更新剩余权重以补偿量化误差。

OBQ 需要 4 小时来量化一个 1 亿参数的模型。为了处理大型 LLMs，该算法

• 每列仅更新一次权重
• 使用惰性批处理以实现高内存吞吐量
• 解决数值不稳定性

量化仅改善模型的内存需求。为了加速推理（$3.2-4.5\times$），实现了特殊的反量化内核。

结果

GPTQ 可以在大约 4 小时内将 OPT 和 BLOOM 量化到每个权重 4 位和 3 位。

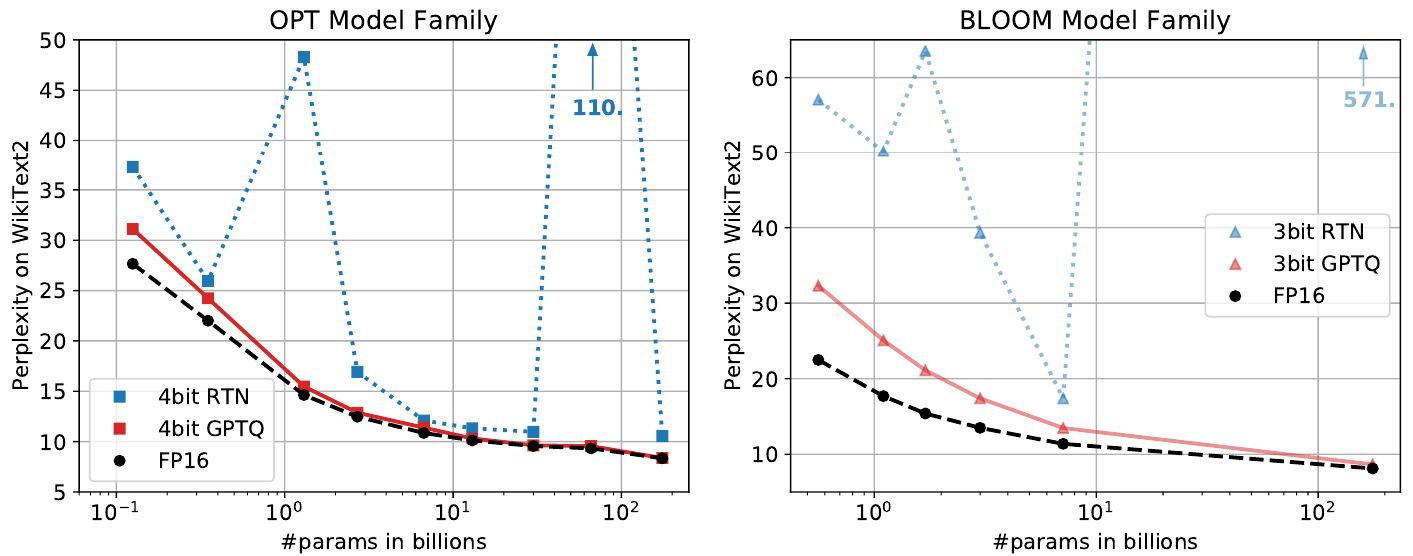
观察结果：

• 最大量化模型的困惑度在 fp16 模型的 1-2 点以内
• 对于较小的模型，差异更大，因为量化不那么重要

数据高效量化

GPTQ 算法确实需要大量高质量数据来优化量化权重，因为它旨在匹配量化模型和原始模型之间的激活。现代量化方法利用不同的假设/指标来实现更高效的数据量化。

• NormalFloat 4-bit [“bitsnbytes” 或 “bnb” 风格] 量化假设权重的某种分布来设计最佳量化级别。它不需要任何数据来量化权重
• Activation-aware Weight Quantization (AWQ) 仅使用激活幅度来选择性地量化权重，从而使其对数据的变化或缺乏更具鲁棒性

基本量化

标准量化将原始表示范围映射到较小的范围，四舍五入到固定（较小）数量的量化级别

$$\mathbf{X}^{\text{Int8}} = \text{round}(c^{\text{FP32}} \cdot \mathbf{X}^{\text{FP32}})$$

其中 $c^{FP32} = \frac{127}{\text{absmax}(\mathbf{X}^{\text{FP32}})}$ 是基于最大值的最佳量化常数。

为了防止异常权重影响最大值，我们可以根据权重分布的分位数选择量化常数，并选择权重矩阵的块进行单独量化。

“BitsnBytes” 或 QLoRA 风格量化

结合了块级和基于分位数的方法。

由于大多数深度学习模型权重是通过归一化训练的，它们大多遵循正态分布。缩放这些权重很容易，因为如果我们假设均值为 0，则只需要一个 $\sigma$ 参数。

这将导致一个缩放的正态分布，其中 Normal Float 数据格式非常有用。在这里，我们定义量化级别，使它们之间的概率质量相等，而不是算术四舍五入。

为了进一步减少内存消耗：块的量化常数（在这种情况下为 $\sigma$ 值）再次量化（双重量化）。

NF4 可能值

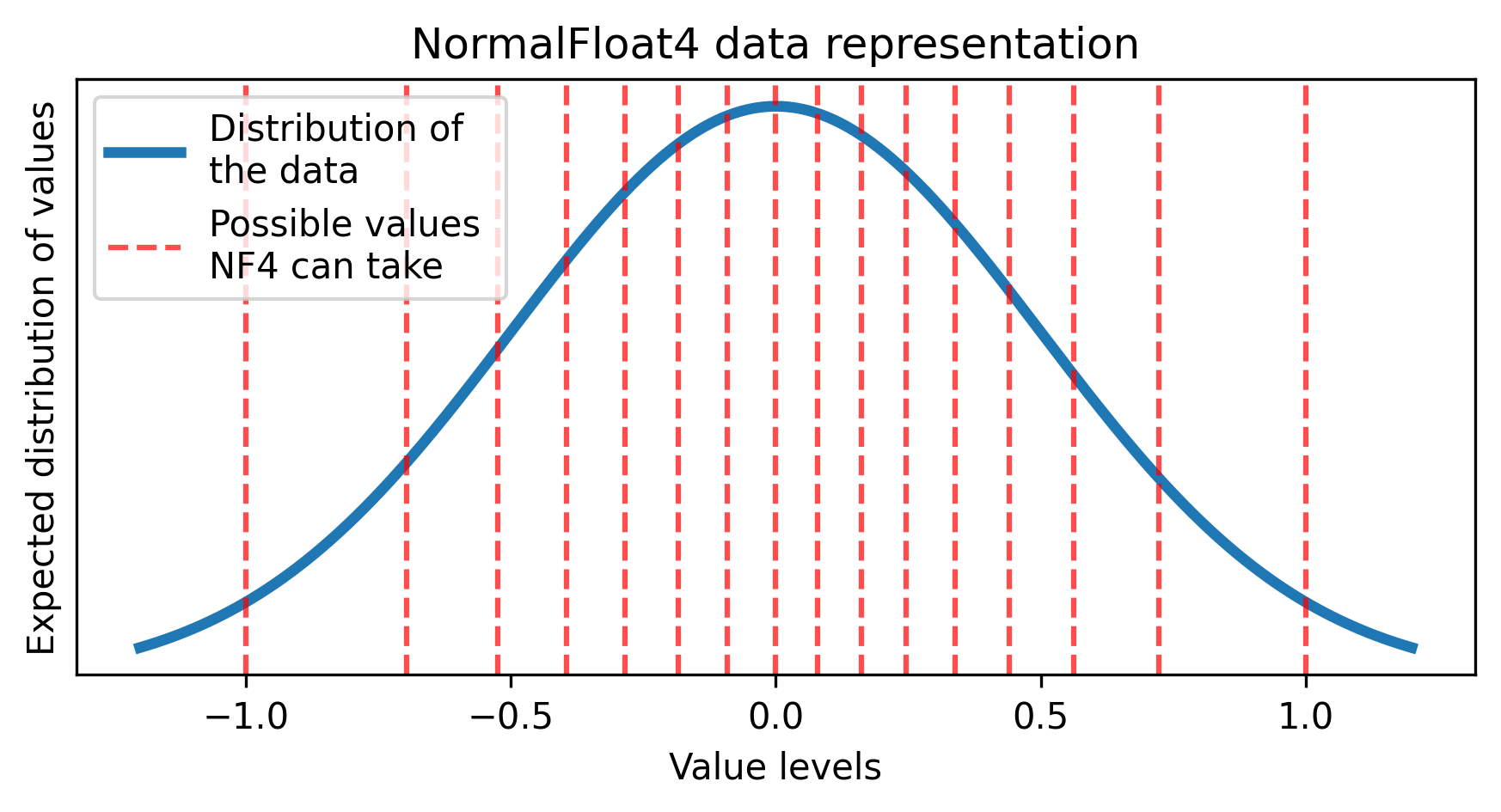
激活感知权重量化

Activation-Aware Weight 是一种数据高效的方法，其主要创新是保持一组显著权重在原始精度（fp16）下，并在量化前按重要性比例缩放权重（同时按此缩放因子划分输入通道）$Q(w) = 1/c \cdot \text{round}(c\cdot w \cdot s)$，而输入则反向缩放传递 $x/s$ 到层。这里我们使用块状线性绝对最大缩放 ($c$) 和通道级缩放因子 ($s$)，该因子由小数据集上的激活幅度确定。

激活幅度计算为：$A_d = \sum_{i=1}^{N} |x_{i,d}|$，其中 $N$ 是数据集中的样本数量，$d$ 是通道索引。通道 $\hat{d} = \text{argmax}_d (A_d)$ 的权重保持为 fp16，其余部分进行量化。

AWQ 基准测试结果

缩放因子 $s$ 为每个通道确定为 $s_d = A_d^{\alpha}$，其中 $\alpha$ 是通过网格搜索找到的可调参数。使用 $\alpha=0$ 意味着没有缩放，而通常考虑最多线性缩放 $\alpha=1$。在量化之前，放大的权重在给定通道上分布得更广，这导致较小的量化误差，同时可能增加其他通道的误差。AWQ 不使用基于梯度的优化，而是在前向传递中使用小数据集进行 $A_d$ 和 $\alpha$ 计算。

高效量化推理

CPU 和 GPU 并不总是为混合精度操作做好准备（因此每个操作可能需要在使用全精度输入之前暂时反量化权重）。因此，需要专门的内核或表示来存储和处理量化模型，以避免内存或计算开销。目前首选 MARLIN 内核。

对于内存高效的权重存储，应使用特定平台的打包数据类型（例如：在 32 位变量中存储 8x 4 位权重）。

高效适应

Efficient Adaptation

动机

自 BERT 以来，通过微调将 LLM 知识转移到 NLP 任务上一直是实现最先进性能的方法。然而，微调在参数上效率低下：每个任务都需要一个新模型。

两个相关概念：

• 多任务学习 在多个任务上微调模型。然而，在微调时可能并非所有任务都可用——我们感兴趣的任务可能会缺失。
• 持续学习 系统旨在从任务流中学习。每当出现新任务时，模型需要能够处理它而不会忘记以前的任务。

适配器

适配器通过以下方式解决了持续学习和微调浪费的问题：

• 向原始模型添加特定任务的小型适配器模块 adapter

• 冻结原始模型的权重

• 在微调期间仅训练适配器模块

• 在 transformer 层的两个子层之后插入适配器

• 将它们初始化为接近身份

• 通过使用瓶颈适配器将 $d$ 维数据投影到 $m$ 维并返回来限制附加参数的数量

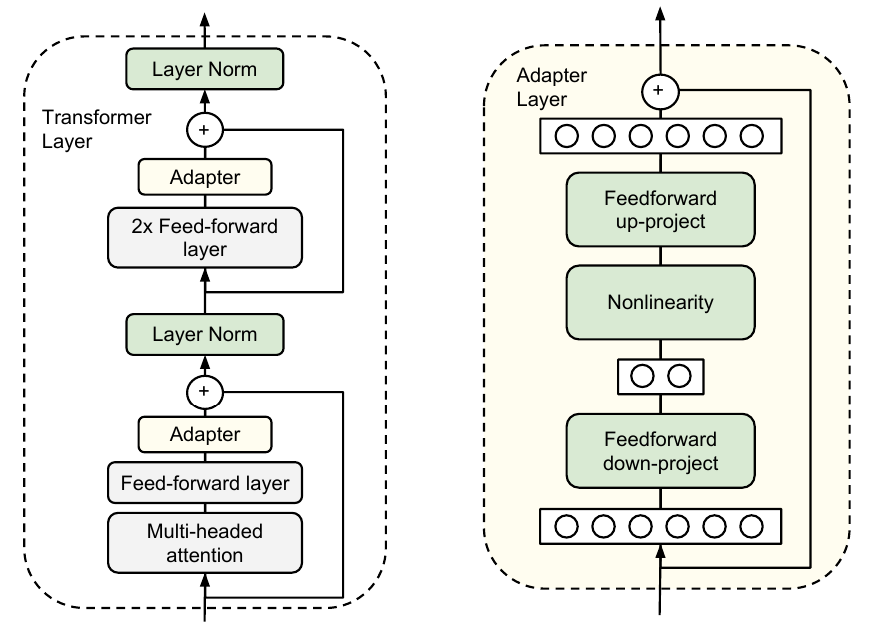
性能

适配器方法的替代方法是仅微调顶层。下层通常计算通用特征；顶层特定于任务。

然而，适配器以两个数量级更少的参数（$1.14-3.6%$）实现了相同的结果：

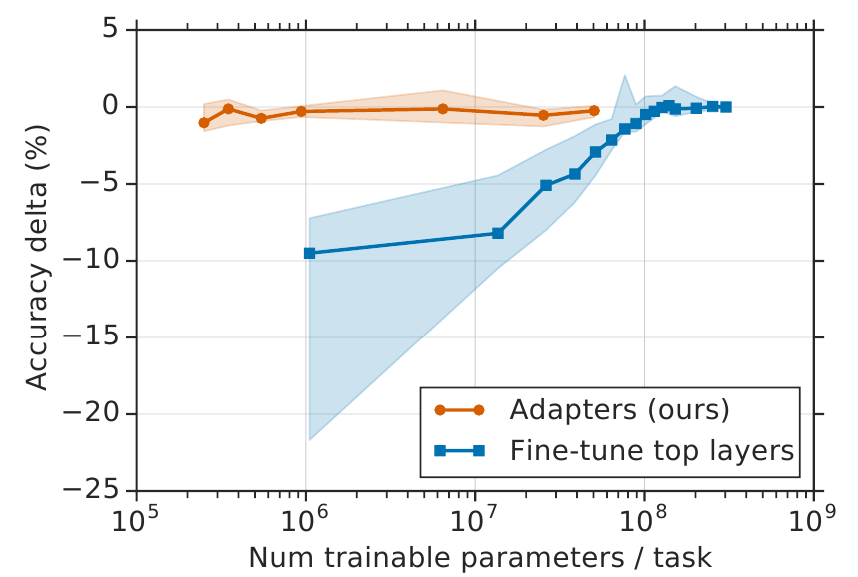
低秩适应 (LoRA)

Low-rank adaptation 通过稍微不同的方式解决了与适配器相同的问题。它不是在原始模型的组件之后添加新的可训练层，而是添加低秩分解矩阵，以并行于原始冻结矩阵表示适应所需的变化：

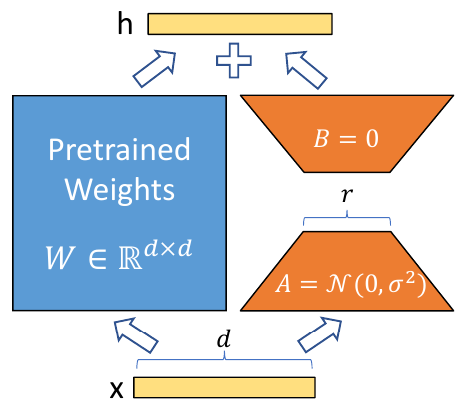
LoRA 类似于适配器：

• 添加小型、低维模块——通常 $r=2$ 或 $4$ 就足够了
• 为每个任务训练一组不同的模块
• 模块大小与适配器相似
• 确保高效微调

然而，有一些关键区别：

• LoRA 仅应用于自注意力矩阵 ($W_k, W_q, W_v, W_o$)
• LoRA 模块可以在推理时与冻结矩阵合并，这不会产生与适配器相比的推理延迟
• LoRA 通常在下游任务上取得略好的结果

内在维度

为什么我们可以使用 SGD 在特定任务的小数据集上微调百万/十亿参数模型，而无需归一化？为什么低秩适应技术（瓶颈适配器、LoRA）适用于微调？Intrinsic Dimensions 可能提供了答案。

目标函数的内在维度是解决优化任务所需的最小维度。在我们的情况下，这转化为：

我们需要多少参数（除了未微调的预训练模型）才能达到至少 $90%$ 的完全微调模型的性能？

数学公式

计算最低维度 $d$ 是不可行的；我们只能通过启发式方法近似。设 $\theta^D$ 为微调模型的 $D$ 维参数，$\theta_0^D$ 为原始模型的参数。那么，我们正在寻找最低的 $d$ 使得

$$\theta^D = \theta_0^D + P(\theta^d)$$

其中 $P: \mathbb{R}^d \rightarrow \mathbb{R}^D$

在原始公式中，$\theta_0^D$ 是完整模型的参数。此公式扩展为考虑多个层。LoRA 在此框架中定义为 $P(\theta^d) = B$。

寻找 $d$

找到 $d$ 的唯一方法是通过超参数搜索。

• 内在维度是下游任务相对于预训练模型的最小描述长度
• 从这个角度看，内在维度与压缩有关，因此它也与模型的泛化能力相关
• 较大的模型允许更小的内在维度

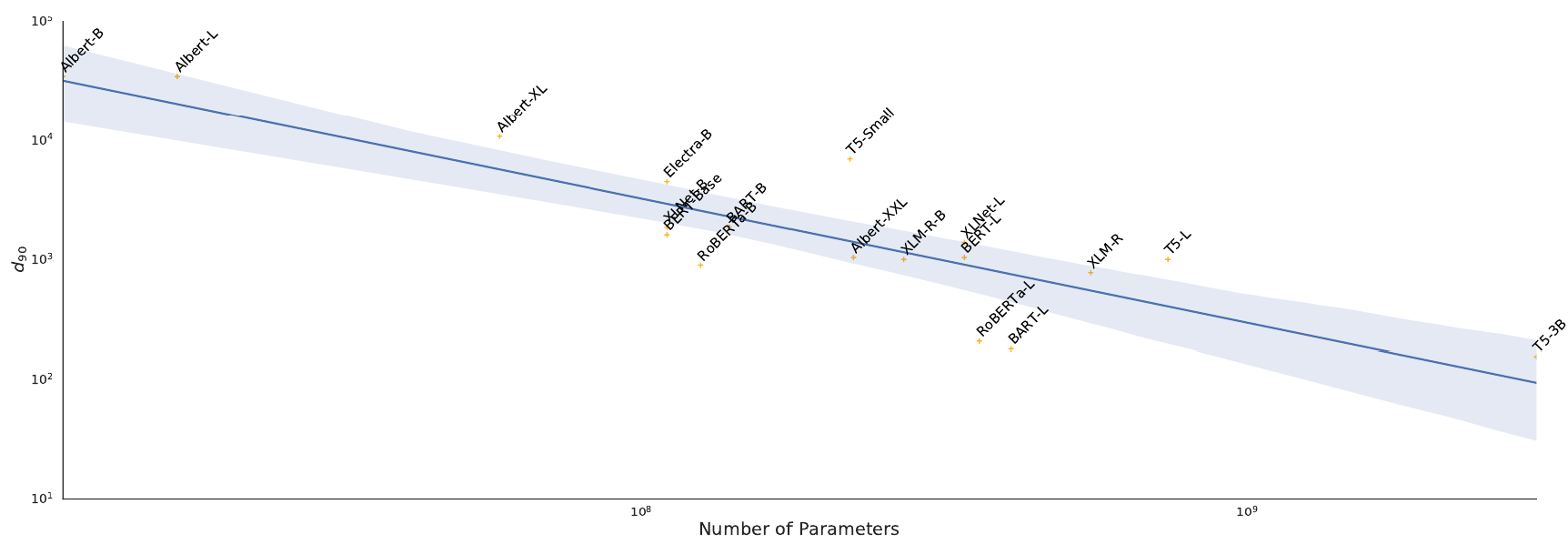
P^*^-Tuning

p^*^-tuning 是一组用于轻量级微调的方法。它的灵感来自 prompting。在这里，可训练的组件是任务特定的自由参数“tokens”，插入到实际输入之前（也称为软提示）。

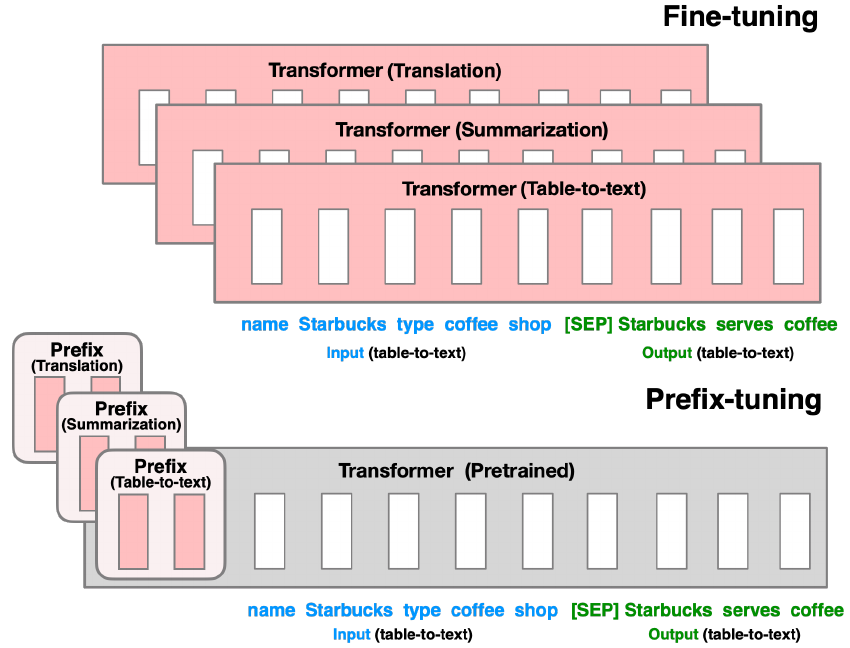
p^*^-tuning 适用于仅解码器和全栈模型。

前缀微调

前缀微调 将软 tokens（前缀）添加到输入嵌入和每一层的输入中。

• 前缀微调需要大约 $0.1%$ 的额外参数
• 与适配器相比，这是 $30\times$ 的减少
• 前缀微调
  • 优于适配器
  • 获得与微调相当的性能
  • 在低数据设置中优于微调

其他方法

提示微调 类似于前缀微调，但提示仅添加到输入嵌入中。

P-tuning 训练一个 LSTM 来生成软提示（不仅仅是前缀）。它在多个数据集上比提示微调高出 $15-20$ 分。

P-tuning V2 对于 Transformer 编码器模型，实际上与前缀微调相同。

PEFT 库

参数高效微调 (PEFT) 库 支持所有这些方法（以及更多）。