NLP-EfficientAttention
高效注意力
动机
Transformer 非常强大,主要得益于 注意力机制,它避免了传统 seq2seq 模型中的瓶颈。然而,注意力机制也有其自身的成本。
回想一下在注意力层中,输入序列中的每个向量 $\mathbf{I} = \langle\mathbf{i}_1, …, \mathbf{i}_n\rangle$ 都会与另一个序列中的每个向量 $\mathbf{X} = \langle\mathbf{x}_1, …, \mathbf{x}_m\rangle$ 进行比较,通过计算(例如)相似度
$$
s(\mathbf{i}_i, \mathbf{x}_j) = \frac{\mathbf{i}^\intercal_i \mathbf{x}_j}{\sqrt{d}}
$$
大多数 Transformer 模型使用 全局注意力,其中(在自注意力层中)$\mathbf{X}=\mathbf{I}$。这意味着
$$
\mathbf{S} = \frac{\mathbf{Q^\intercal}\mathbf{K}}{\sqrt{d}}
$$
矩阵的计算和存储复杂度将是二次的:$\mathcal{O}(n^2)$。这限制了
- Transformer 可以使用的 上下文
- 适合 GPU 内存的模型 大小
- 模型的 吞吐量,因此增加了其碳足迹
在下文中,我们将看到试图解决这些问题的技术。
稀疏 Sparse 注意力
稠密 Dense 层中的稀疏性
在 CIFAR-10 数据集上训练了一个 128 层的图像 Transformer,并观察到在许多层中,注意力模式是稀疏的:

因式分解自注意力
注意力层可以通过 连接模式 (connectivity pattern) $S = {S_1, …, S_n}$ 来表征,其中 $S_i$ 是第 $i$ 个输出向量关注的输入索引集。对于常规自注意力,这是 $S_i = {j: j \leq i}$。
Factorized 自注意力
- 有 $p$ 个独立的头,而不是常规注意力的 1 个头(或多头注意力的 $\times p$)
- 对于第 $m$ 个头,$S_i = A^{(m)}_i \subset {j: j \leq i}$,是稠密注意力的一个 子集
- 这些是连续应用的:$A_i = A^{(1)}_i \cdots A^{(p)}_i$
如果 $|A^{(m)}_i| \propto \sqrt[p]{n}$,则因式分解自注意力的复杂度为 $\mathcal{O}(n\sqrt[p]{n})$。从现在起,假设 $p=2$。
因式分解 patterns
如果 $A$ 可以连接所有输入和输出位置,则因式分解是 有效的。两个例子:
跨步 Strided 注意力
- 给定一个 步长 $l \approx \sqrt{n}$
- $A^{(1)}_i = {i-l, i-l+1, …, i}$(前 $l$ 个位置)
- $A^{(2)}_i = {j: (i - j)\mod l = 0}$(每 $l$ 个)
固定注意力
- $A^{(1)}_i = {j: (\lfloor j/l \rfloor = \lfloor i/l \rfloor)}$(每个输出向量关注其块)
- $A^{(2)}_i = {j: j\mod l \in {l-c,l-c+1,…,l} }$(未来的输出关注块中的最后 $c$ 个项目)
固定注意力更适合文本,跨步注意力更适合图像。
两种稀疏注意力类型的示意图:

架构
$p$ 个头可以通过三种方式集成($W_p$ 是 FF):
- 每层一个头:
$\textrm{attention}(X) = W_p \cdot \textrm{attend}(X, A^{(r\mod p)})$ - 合并头:
$\textrm{attention}(X) = W_p \cdot \textrm{attend}(X, \bigcup^p_{m=1}A^m)$ - 多头($n_h$)注意力:
$\textrm{attention}(X) = W_p\bigl(\textrm{attend}(X, A)^{(i)}\bigr)_{i \in {1, …, n_h}}$
通过这些变化,可以训练具有数百层和/或非常长上下文(文本为 12,160,音乐为 $2^{20}$)的 Transformer。
其他稀疏注意力变体
多头注意力选项也适用于其他稀疏注意力模式:
- 全局注意力:一些全局 token 关注整个序列;
(注意:这种稀疏全局注意力不同于密集全局注意力,因为只有少数 token 关注所有内容) - 随机注意力:对于每个查询,计算一组 $r$ 个随机键,查询关注这些键
- 窗口注意力:仅关注固定半径内的局部邻居
Big Bird
Big Bird 模型结合了所有这些线性注意力类型,以显著增加输入 token 的数量,而不会显著改变内存需求:
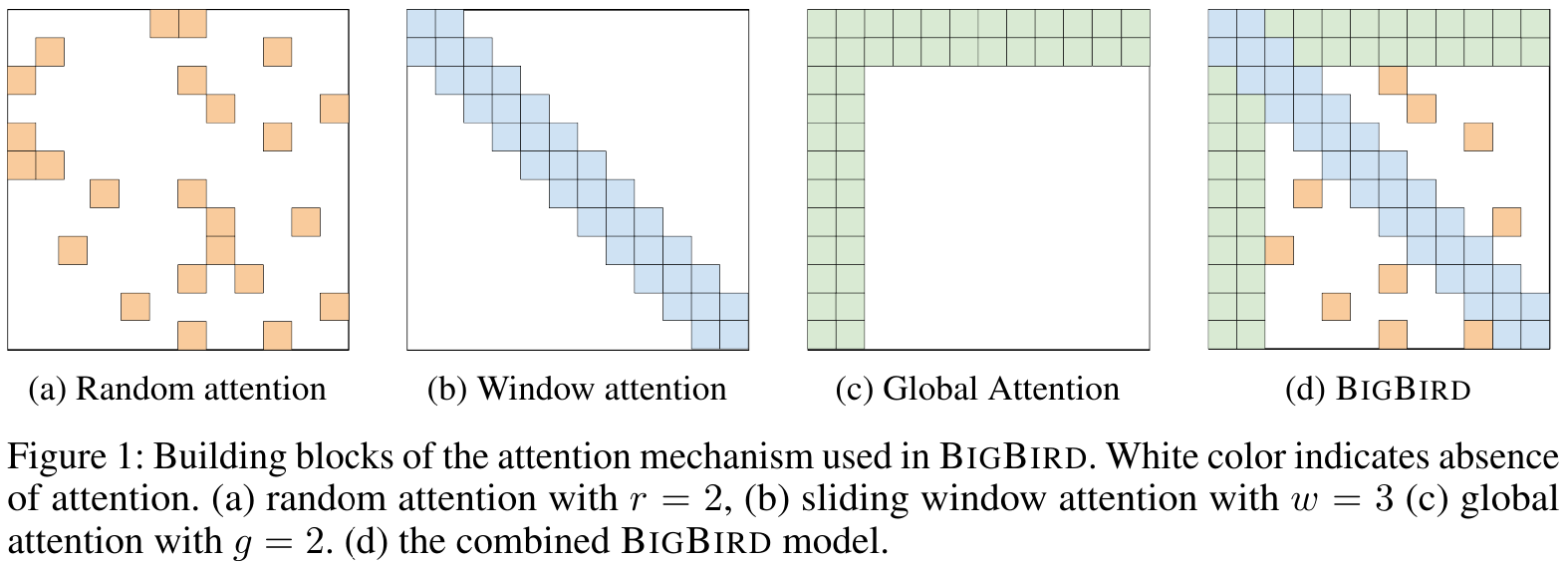
长序列
长序列的外推
RNN 可以在短序列上训练,但在推理期间可以在更长的序列上运行。Transformer 解码器可以像这样 extrapolate,但效果不佳:
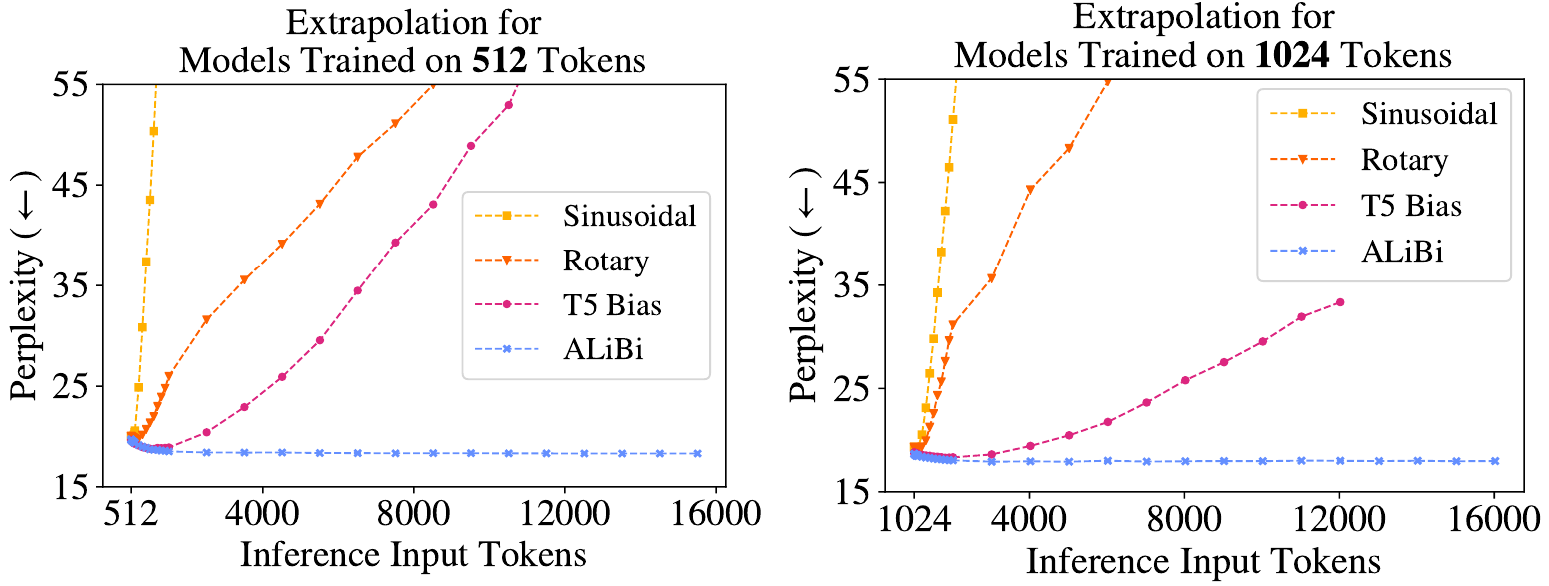
位置方法
测试了以下位置方法:
- 正弦位置嵌入:默认的 Transformer 嵌入。性能在增加 $5-10%$ 额外 token 后下降
- 旋转位置嵌入 (RoPE):例如在 GPT-3 中使用。将Sinusoidal嵌入应用于每个注意力层中的 $\mathcal{K}$ 和 $\mathcal{Q}$(但不应用于 $\mathcal{V}$ 和嵌入)。可以外推到 $+10-40%$ 的 token,但速度较慢
- T5 偏置:一种相对位置方法,根据每层中键和值对之间的距离向 $\mathcal{V}$ 添加一个 学习 偏置。嵌入未被修改。可以外推到 $+80-120%$,但速度非常慢

ALiBi
ALiBi (Attention with Linear Biases) 是一种简单的方法,它根据查询-键距离添加一个静态(非学习)偏置:
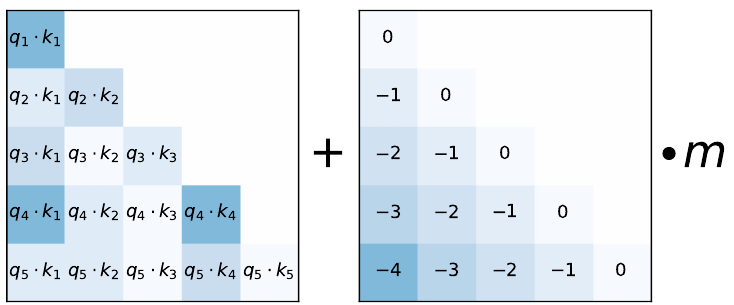
$$ \textrm{softmax}(\mathbf{q}_i\mathbf{K}^\intercal + m\cdot[-(i-1),…,-1,0]) $$
对于 $n$ 个头,斜率形成一个几何序列,范围在 $\bigl(1, \frac{1}{2^8}\bigr]$ 之间;例如,对于 8 个头,斜率为 $\frac{1}{2^1}, …, \frac{1}{2^8}$。
具有 ALiBi 的模型可以轻松地将其训练上下文($L$)外推到 $2-10$ 倍,通常在 $2L$ 时表现最佳!
RoPE 的分析
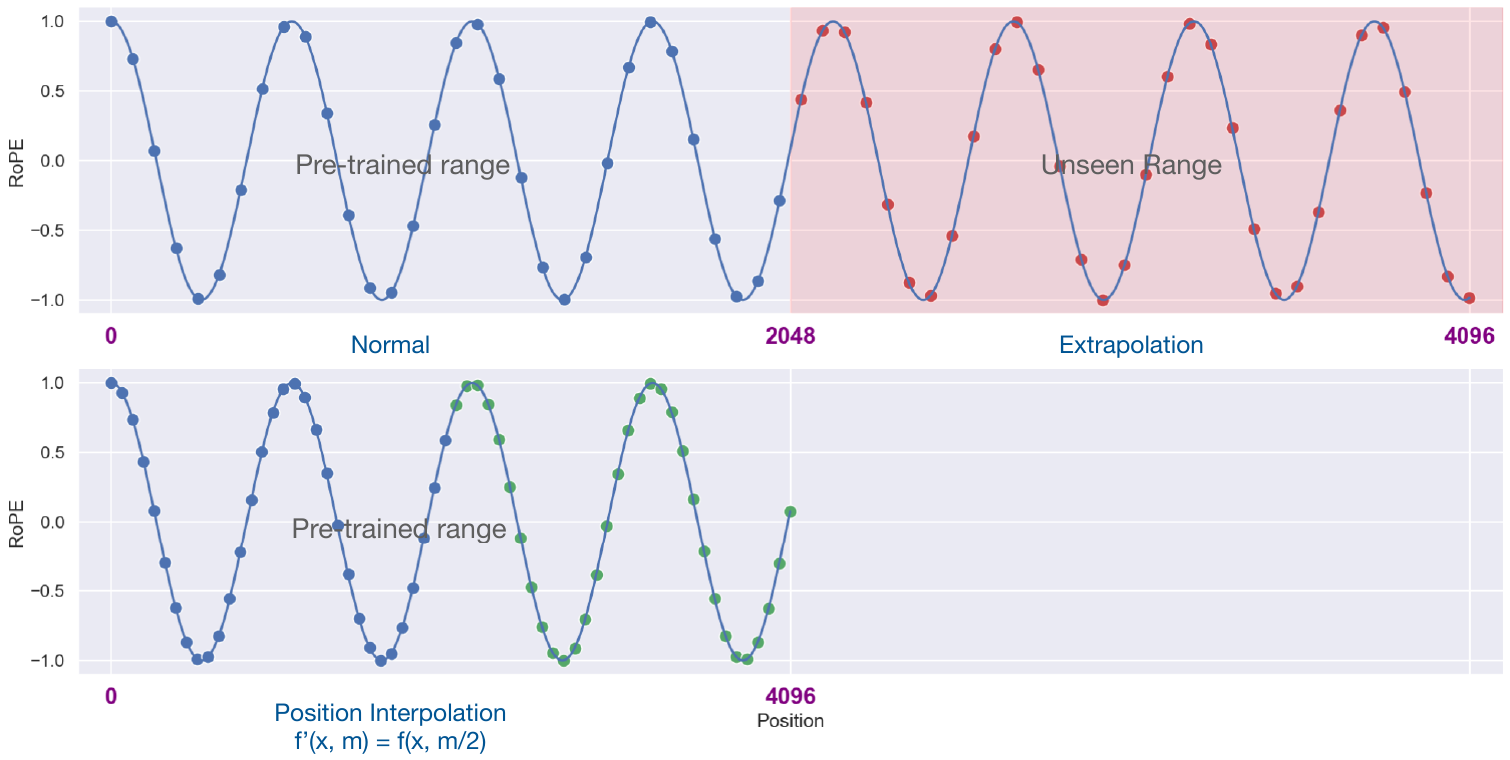
为什么 RoPE 的直接外推不起作用?
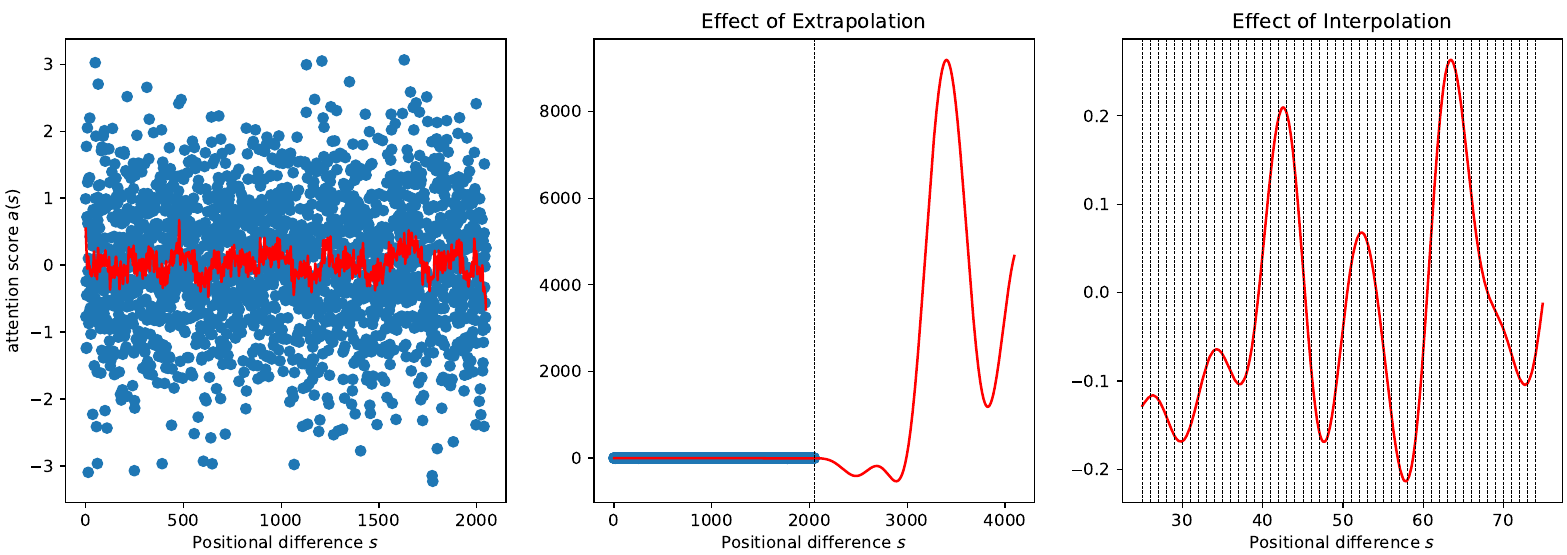
虽然在 RoPE 中自注意力得分应该只取决于两个位置之间的相对距离,但在训练上下文 $L$ 之外(中间),它会变得任意大。
三角函数族是一个通用 approximator,可以拟合任意函数。由于我们只在 $[0, L]$ 范围内训练 RoPE,我们不知道函数在 $L$ 以上的表现。
位置插值
位置插值(Position Interpolation,PI)通过将更长的上下文窗口 $L’$ 映射到 $L$ 来解决这个问题。
- 每个位置 $m’ \in L’$ 被转换为 $m = m’\frac{L}{L’}$
- 然后对模型进行 1000 步的微调
结果
实验表明
- Llama 的 2k 上下文可以扩展到 32k;
- 针对 $L’=8k$ 微调的模型在原始 $L$ 范围内表现出最小的退化($2%$)。
其他 实现类似策略的报告表明,即使没有微调,也可能实现 $2-4\times$ 的扩展。
Flash 注意力
理论与实践
许多近似方法(例如稀疏注意力)设法减少了 FLOPs,但没有减少实际时间。这是因为忽略了内存访问速度(IO)。
常规注意力通过物化从 $Q, K, V \in \mathbb{R}^{N\times d}$ 计算输出 $\mathbf{O} \in \mathbb{R}^{N\times d}$
$\mathbf{S} = \mathbf{QK}^\intercal \in \mathbb{R}^{N\times N}$
$\mathbf{P} = \textrm{softmax}(\mathbf{S}) \in \mathbb{R}^{N\times N}$
$\mathbf{O} = \mathbf{PV} \in \mathbb{R}^{N\times d}$
在 GPU 的高带宽内存(HBM)中。这是因为
- 这些是 PyTorch / TF 中的单独指令
- 这些矩阵在反向传播 backpropagation 中是必需的
GPU 层次结构
主要问题是
- 与计算和 SRAM 相比,HBM 非常慢
- softmax、dropout、norm 操作都是内存受限的,需要 $\mathcal{O}(N^2)$ 的 HBM 访问
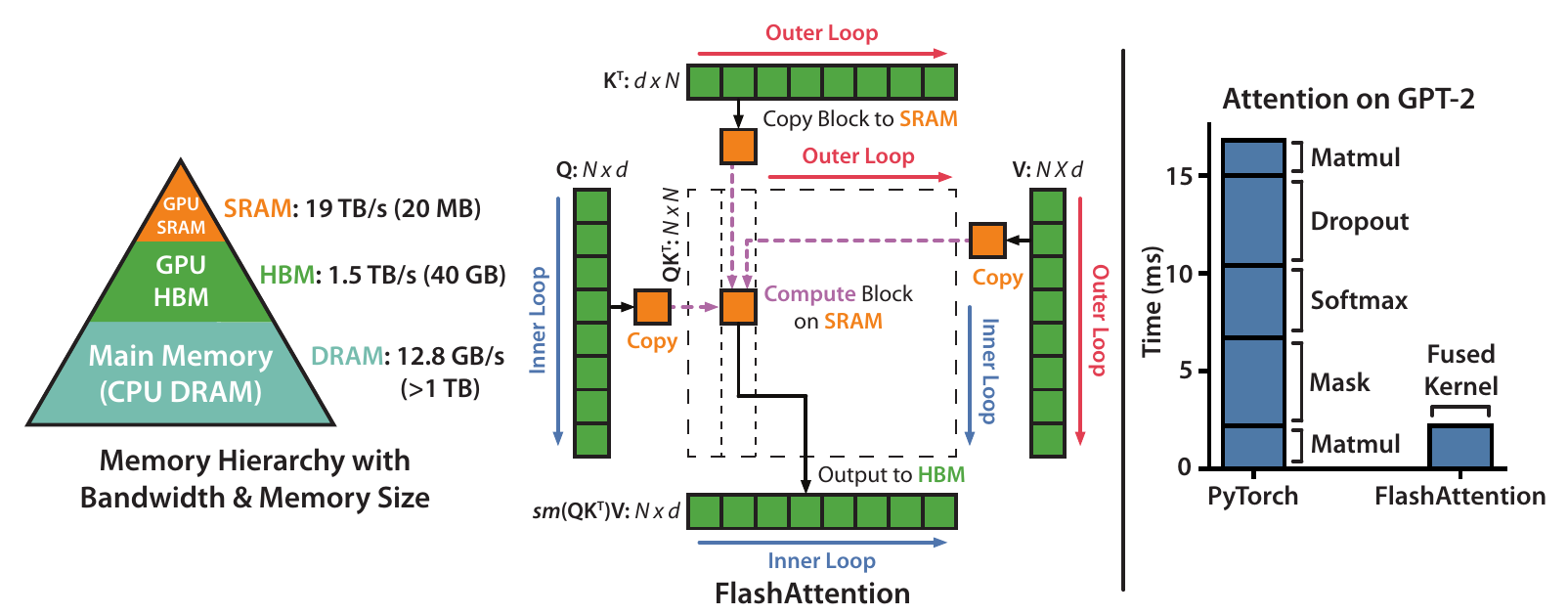
FlashAttention 通过优化内存访问解决了这些问题。
FlashAttention
优化:
- $\mathbf{S}$ 和 $\mathbf{P}$ 使用平铺 tiling逐块计算
- 它们从未在 HBM 上物化,而是在反向传播时重新计算
- 单个块的所有操作在单个内核中同时执行
尽管重新计算会导致更多的指令(FLOPs),但 HBM 访问的总次数减少了
- 从 $\Theta(Nd+N^2)$(标准注意力)
- 到 $\Theta(N^2d^2M^{-1})$(FlashAttention)
其中 SRAM 大小 $M > d^2$ “多次”。
FlashAttention
- 相对于标准注意力,实现了 $15%$(与 BERT 速度记录相比)到 $3\times$(GPT-2)的加速
- 内存随 $N$ 线性扩展
- 允许更长的上下文(GPT-2 为 4k)
稀疏 FlashAttention
- 块稀疏注意力可以通过 FlashAttention 加速
- 更快(取决于稀疏性,$2-4\times$),上下文可达 64k
FlashAttention2 通过优化 GPU 线程之间的作业分配,再次实现 $2\times$ 的加速
NLP-EfficientAttention