NLP-Contrastive
对比表征学习
自监督学习
主要目标
自监督学习(Self-supervised learning)旨在从数据本身获取监督。
“从一切中预测一切。”
Yann Lecun
数据是部分已知,部分未知的。
利用数据的潜在结构(例如语言建模中的顺序性)。
为什么不是强化学习?
试错法无效。
优势
自监督学习:
- 降低标注的成本和复杂性
- 增加系统的额外泛化 generalization 能力
- 使得可以利用数据的内部结构
- 能够重建控制输入集的潜在 latent 变量
基于能量的建模
基于能量的建模(Energy-based modeling)是大多数 SSL 方法的统一原则。
EBM 解决了 $L_2$ 类损失的“平均问题”。
- 想象一个有多个可行输出的情况(例如 Skipgram 模型中的相邻词)
- 损失将对这些单个输出的“平均值”最小化
- 我们希望损失函数对每一个可行解都接近最小
能量函数
能量函数 $F(x, y)$ 在 $x \in X$ 输入空间和 $y \in Y$ 输出空间上设计来解决这个问题,其中低能量意味着可行解。
这种模型的推理可以通过:$\hat{y} = argmin_y F(x, y)$
需要注意的是,多个 $\hat{y}$ 可能是可行的!
能量函数 $F(x, y)$ 衡量 $x$ 和 $y$ 之间的兼容性。
作为概率模型的 EBM
使用 Gibbs-Boltzmann 分布,生成(联合“分布”)EBM 可以转换为判别概率模型:
$P(y|x) = \frac{e^{-\beta F(x, y)}}{\int_{\acute{y}} e^{-\beta F(x, \acute{y})}}$
这里 $\beta$ 是一个正常数,$\acute{y} \in Y$。
多模态 EBM 架构
EBM 对于创建联合 Multimodal 表示非常有用。
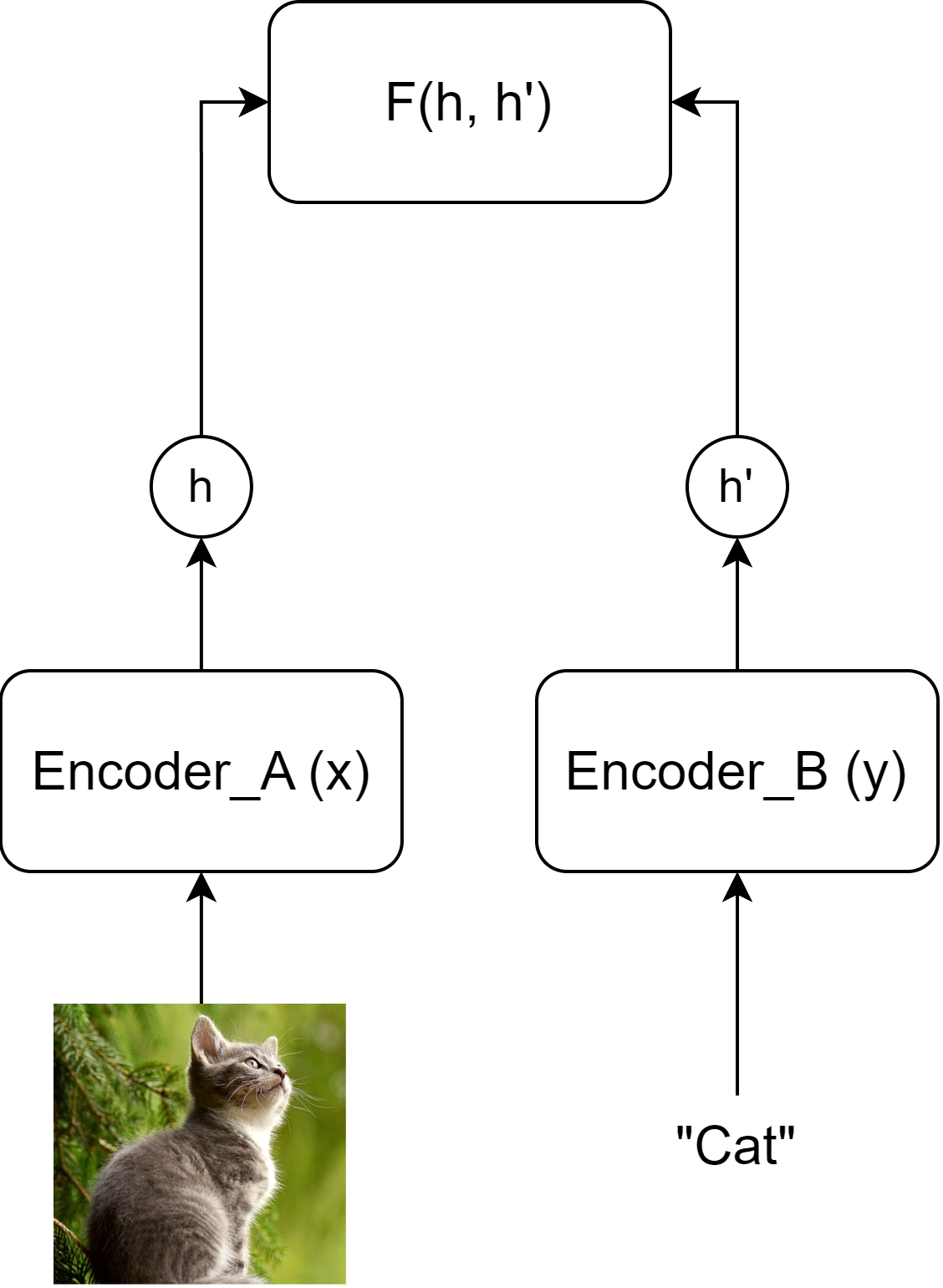
潜 Latent 变量可以用于生成过程(例如扩散 diffusion)。$z$ 是一个独立的“解释 explanatory”变量。可以通过对 $y$ 和 $z$ 的联合最小化进行推理。
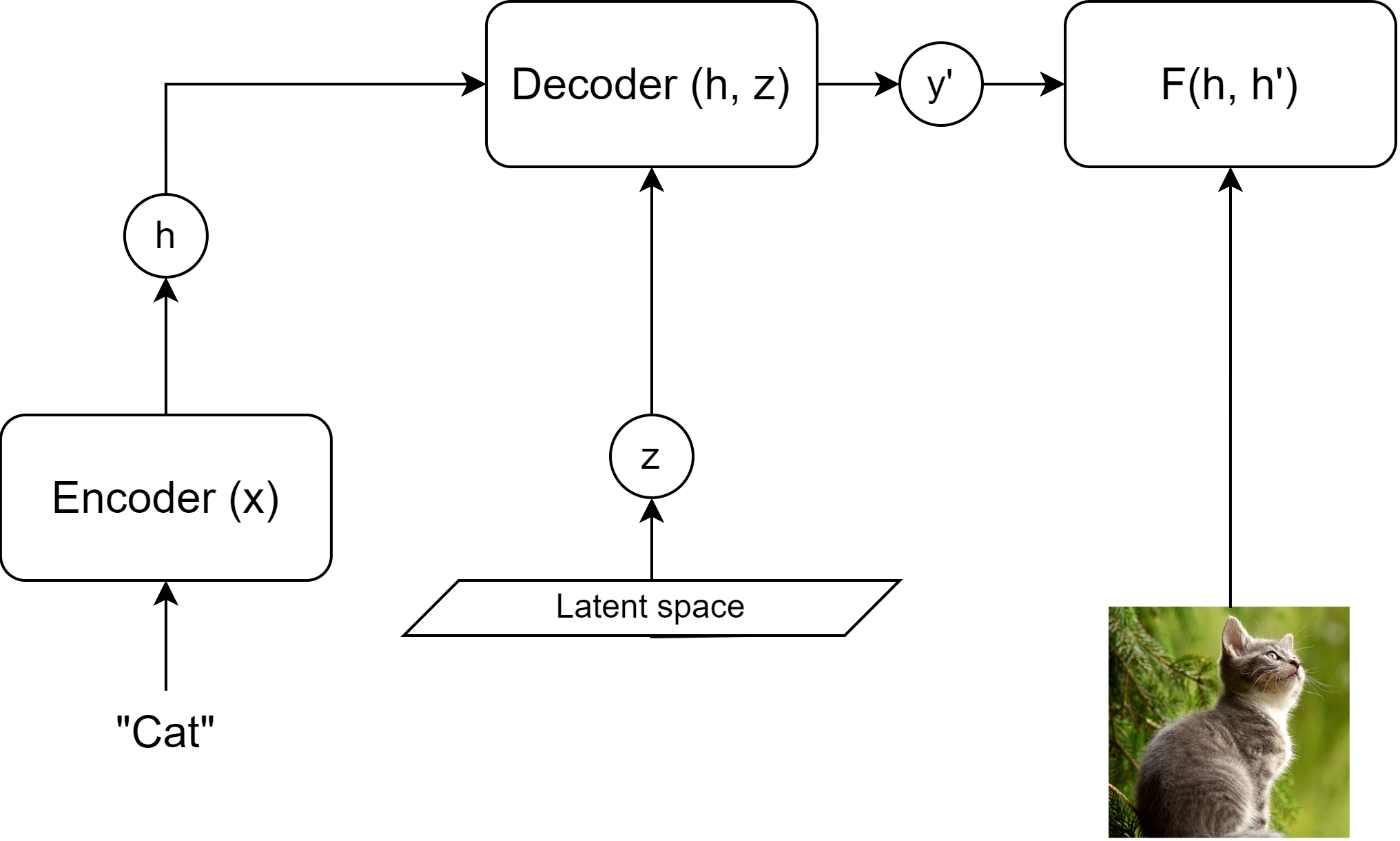
EBM 的学习方法
主要目标:为可行的 $x$-$y$ 对获取低能量,同时为不兼容的对保持高能量。
对比方法
- 为每个兼容对(即数据集的正元素)降低 $F(x, y)$
- 为每个其他可能的组合(即负示例)提高 $F(x, y’)$
主要目标:为可行的 $x$-$y$ 对获取低能量,同时为不兼容的对保持高能量。
正则化方法
- 确保低能量区域的范围有限或最小化
- 正则化、量化、聚类等
主要目标:为可行的 $x$-$y$ 对获取低能量,同时为不兼容的对保持高能量。
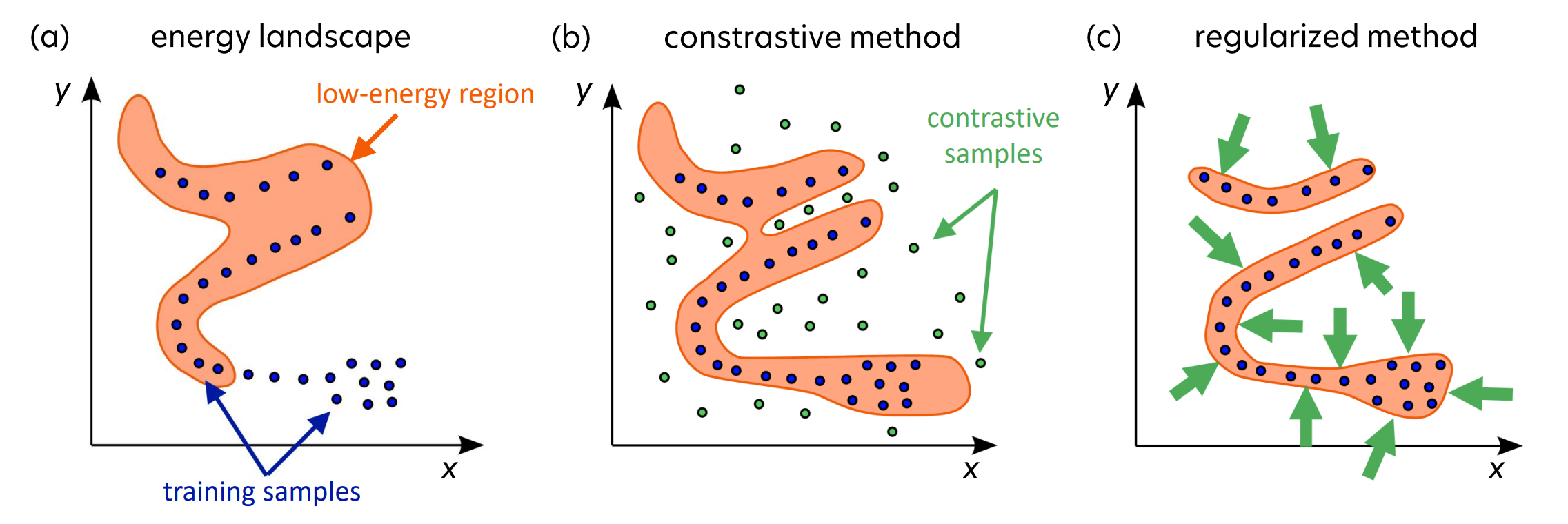
对比学习及其变体
学习方法
对比学习通常包括以下主要步骤:
- 选择一个 $q$ 查询并从正样本分布 $k^+\sim p^+(.|q)$ 和负样本分布 $k^-\sim p^-(.|q)$ 中采样
- 应用模型变换,将 $\mathcal{X} \rightarrow \mathcal{R}^N$ ,其中 $N$ 是结果嵌入维度,$x \in \mathcal{X} | x = (q, k)$
- 使用基于能量或概率的方法对正负样本对进行评分
- 参数更新
评分函数
评分函数是损失计算的核心,由所需嵌入空间的属性决定。它们是简单的函数,例如:
- L1 或 L2 距离
- 点积
- 双线性模型 $S(q, k) = qAk$
基于距离和概率的损失函数建立在这些度量之上。
基于距离的损失函数
对 Pair 损失
$\mathcal{L}_{pair} = \begin{cases} ||q-k^+||_2^2\ max(0, m-||q-k^-||_2^2) \end{cases}$
其中 $m$ 是围绕 x 的预定义边距。这最小化了正样本的距离,并尝试将负样本的距离推到边距之外。
三元组 Triplet 损失
$\mathcal{L}_{triplet} = max(0, ||q-k^+||_2^2 - ||q-k^-||_2^2 + m)$
这种方法强制正样本和负样本之间的相对距离。
基于 Softmax 的概率损失函数
动机:正确分类pairs。
作为使用评分函数 $S(.,.)$ 的分类问题,我们可以将其表述为:
$p(k^+|q) = \frac{exp(S(q, k^+))}{\sum_k exp(S(q, k))}$
引入负采样到过程中,我们可以避免计算所有 $k$ 的分母。相反,我们将计算重新表述为一个二元问题。
噪声对比估计
Noise Contrastive Estimation,如果我们从均匀分布中更频繁地采样负例 $M$ 次,则对对是正例 (C=1) 的概率为:$p(C=1|q,k) = \frac{p(k^+|q)}{p(k^+|q)+m\cdot p(k^-|q)}$
因此,二元分类损失是(使用负对数似然)对所有可能对的:
其中 $p^-(.|q)$ 是噪声(负样本)分布,$p^+(.,.)$ 是正分布。
InfoNCE
我们可以构建一个包含多个负例和一个正例的集合 $K = {k^+, k^-_1, k^-2, …, k^-{M}}$,而不是二元分类。然后修改后的任务是确定哪个元素是正例。这导致了一个类似 softmax 的度量,称为 InfoNCE:
为什么它有效?
使用 InfoNCE 类损失函数训练模型 $f$ 反转(解码)数据生成的未知生成过程 $g$。因此,我们数据背后的潜在分布被重建并变得可访问。
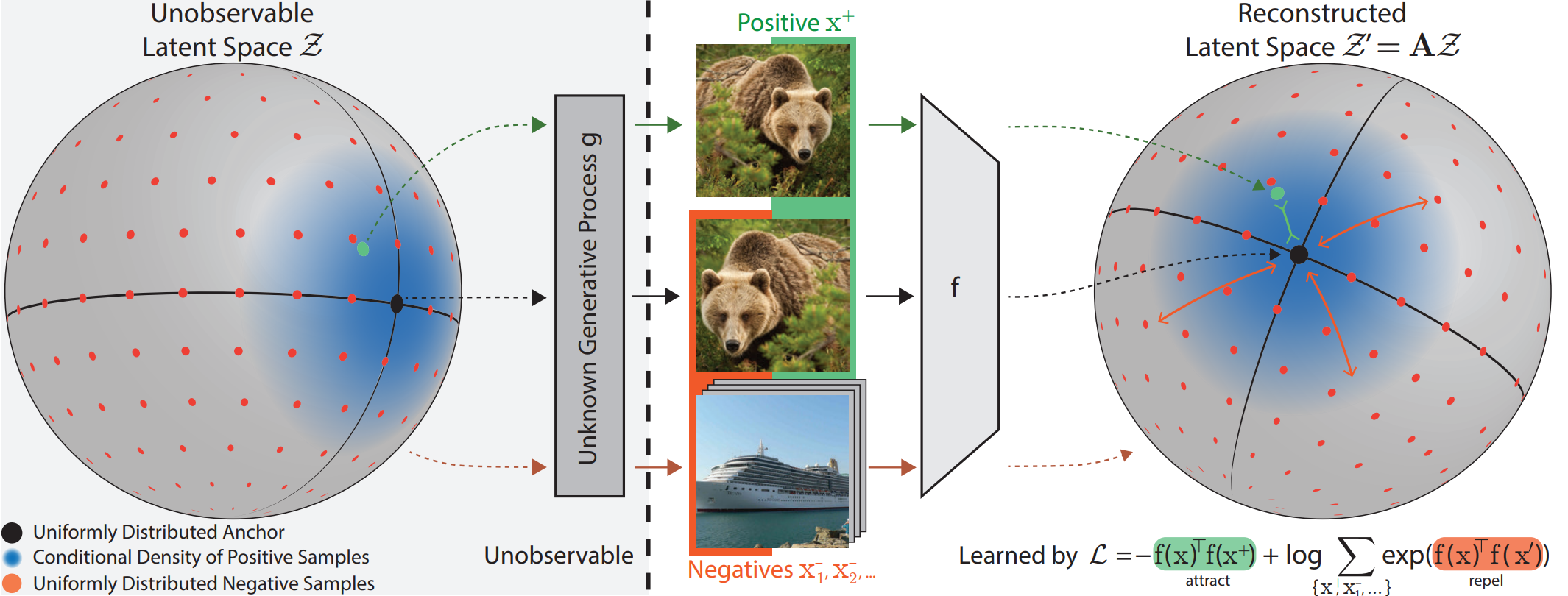
采样示例
数据生成过程可以包括广泛的自监督过程,例如:
- 邻域信息(空间或时间)
- 掩蔽
- 各种增强(视觉或音频噪声等)


添加标签监督
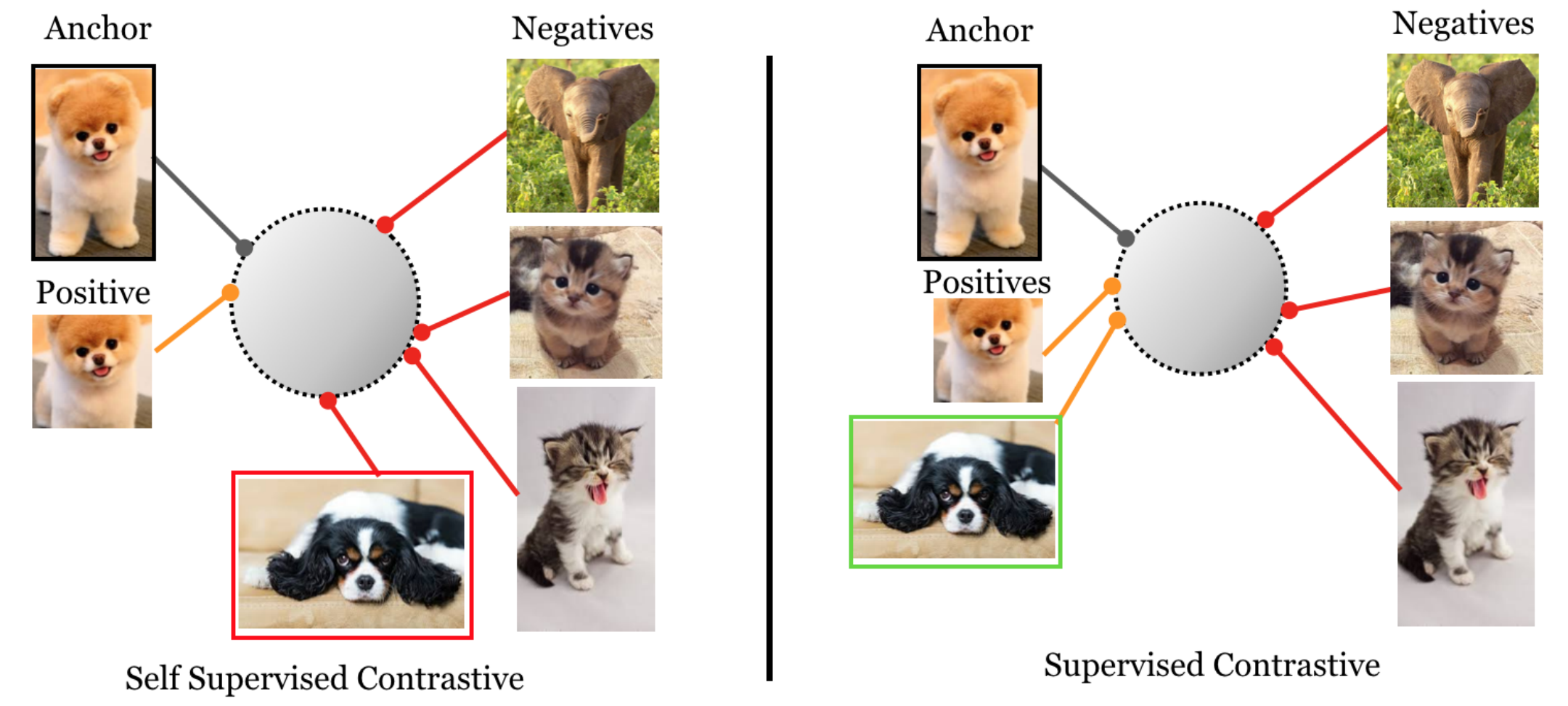
通过结合标签信息(添加经典监督)也可以进行数据生成。在这种情况下,正常的 InfoNCE 方程将发生变化,因为存在多个正样本。这导致了 InfoNCE 项的总和。在对数内和对数外有两个变体。
其中 $J$ 是批处理元素的集合,$q$ 是选定的查询元素,$I$ 是不包括 $q$ 的批处理元素集合,$P(q)$ 是与 $q$ 具有相同标签的元素集合。
其中 $J$ 是批处理元素的集合,$q$ 是选定的查询元素,$I$ 是不包括 $q$ 的批处理元素集合,$P(q)$ 是与 $q$ 具有相同标签的元素集合。
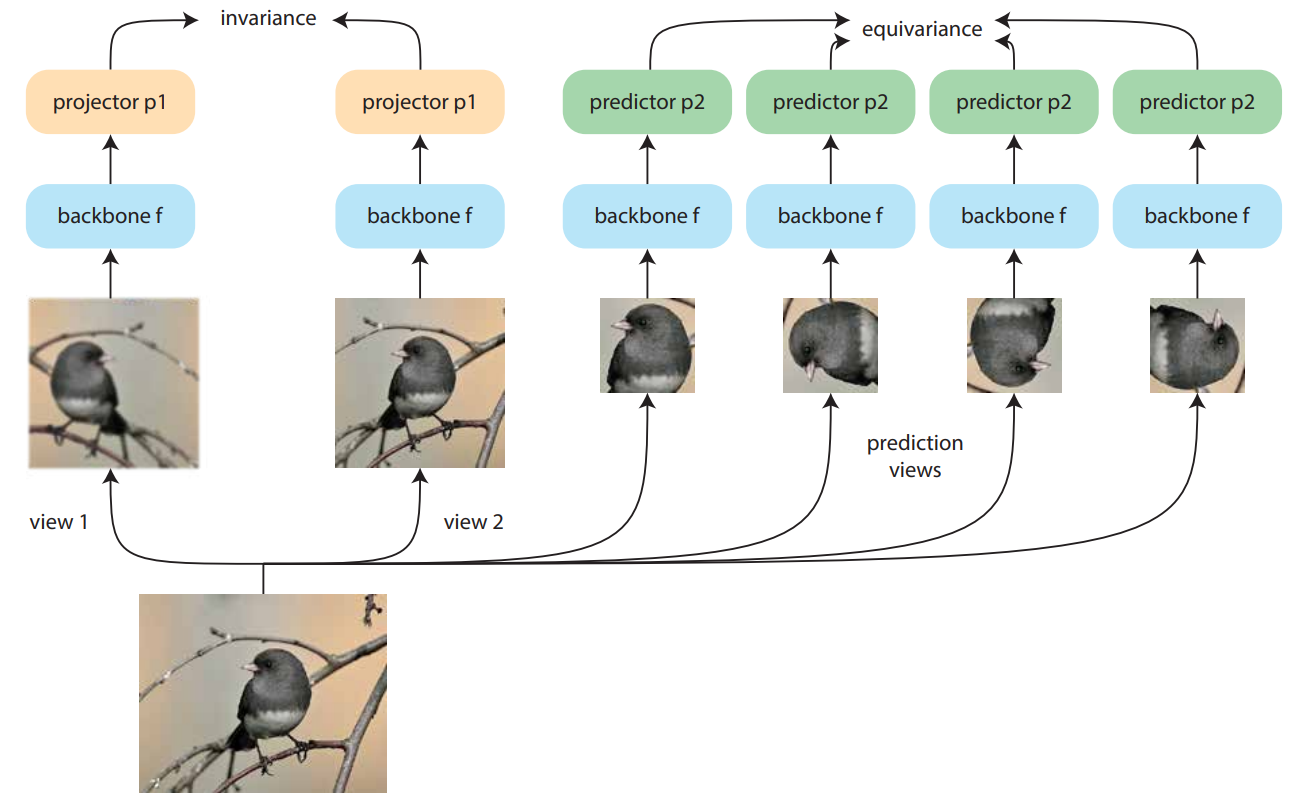
不变性和等变性特征
在标准对比学习中,正样本对具有所需的不变性。$S(q, k)$ 应该很高。当 $q=k$ 时,标准相似性度量最能产生这种行为。这种行为将抵消两个原始输入 $x_q$ 和 $x_k$ 之间的某些差异的影响。
令 $T(\cdot)$ 变换表示这种差异,$f(\cdot)$ 表示我们用 CL 训练的函数(或网络)。在不变的最优情况下:
$x_k = T(x_q) \rightarrow k = q$
在某些情况下,我们希望在嵌入空间中保留这种变换。这意味着我们需要在嵌入空间中与输入空间中相同或相似的变换($\acute{T}(\cdot)$)。
$x_k = T(x_q) \rightarrow k = \acute{T}(q)$
NLP 中的对比方法
Word2Vec 作为对比学习
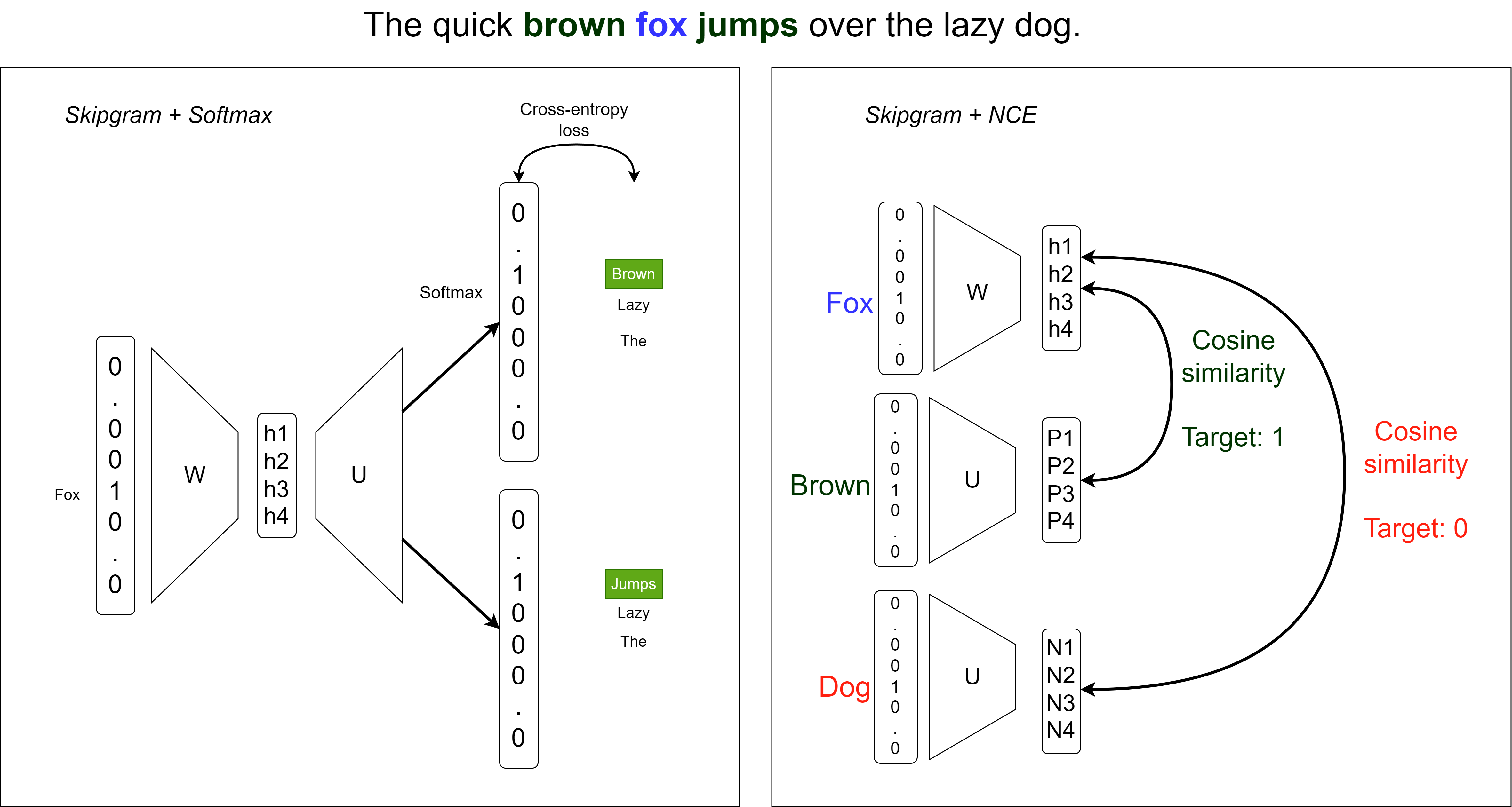
将 skipgram 重新表述为多编码器联合嵌入类型的自监督问题。
我们使用噪声对比估计损失(Noise Contrastive Estimation)而不是 Softmax。
正样本对最大化相似性(根据 EBM 建模最小化能量)。
负样本对最小化相似性(根据 EBM 建模最大化能量)。
BERT 下一句预测
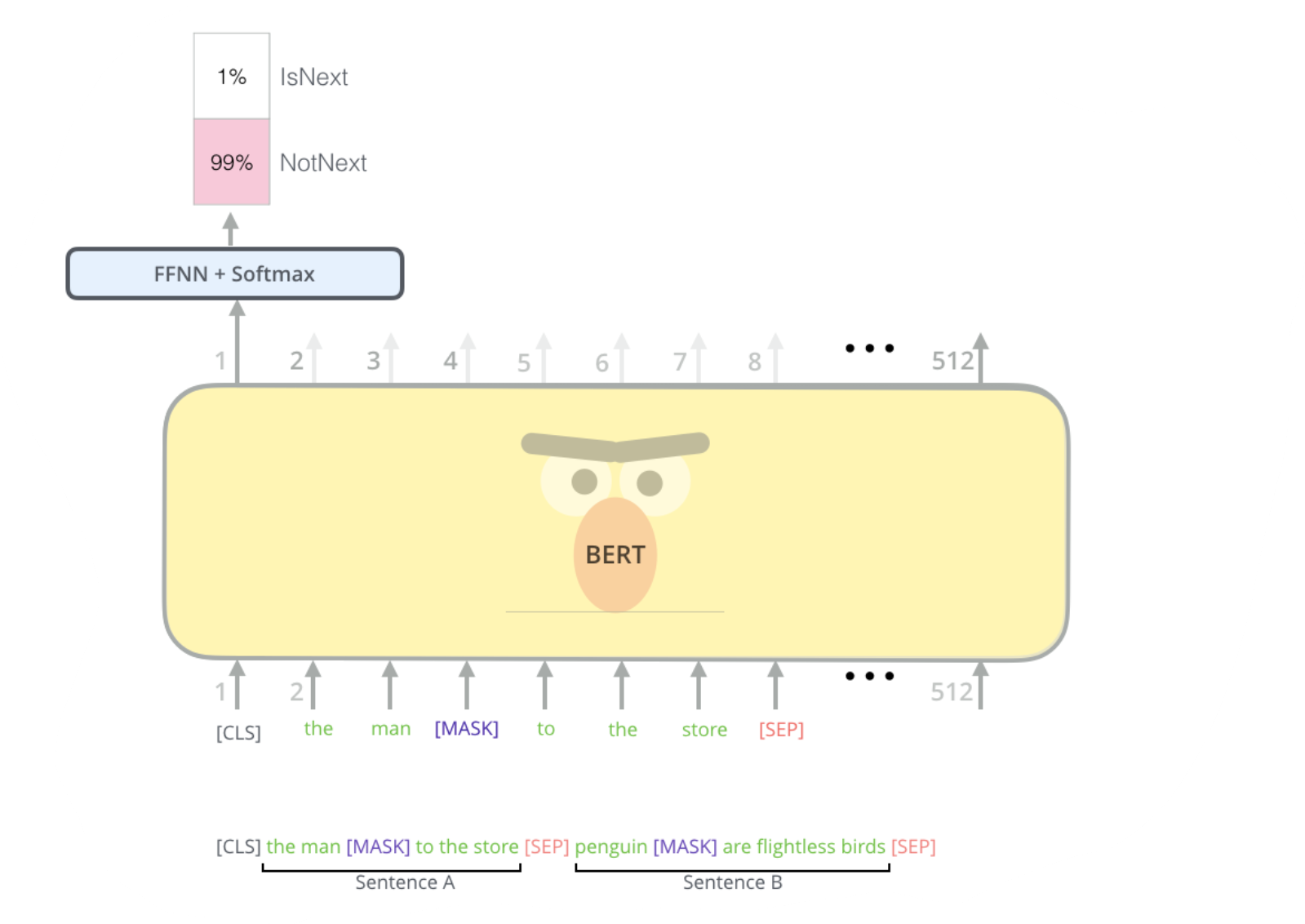
文本嵌入模型
预训练和微调的语言模型可用于生成文本的语义嵌入。
- 这在一般语言语义方面是有利的
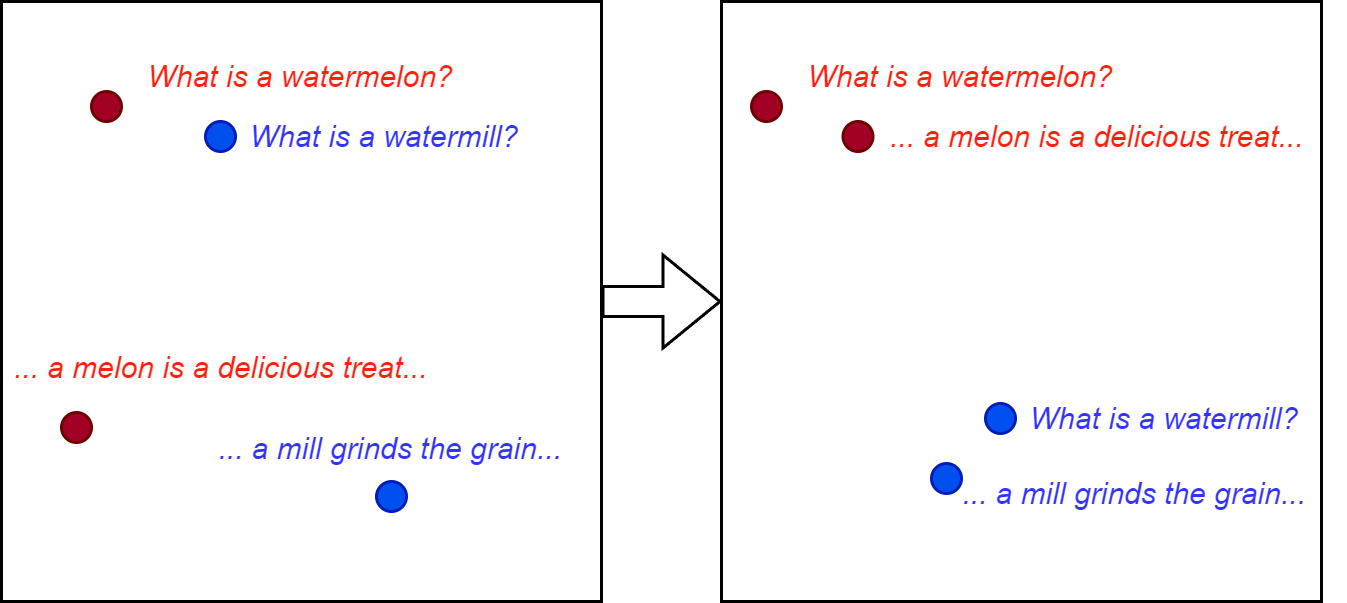
在领域相关的嵌入或多任务嵌入的情况下,对比微调附加的自监督任务非常有用。
这些任务可能包括:
- 检索,重新排序(根据查询查找/排序文档)
- 聚类(在嵌入空间中创建聚类)
- 文本分类
- 摘要
- 去重
对比多模态方法
CLIP
对比语言-图像预训练
问题:视觉分类器受限于有限的监督标签集
解决方案:使用自然语言描述视觉特征,尝试实现零样本/少样本学习
数据:来自网络爬虫的(图像,文本)对(甚至是文件名),包括 Instagram、基于 Wikipedia 的图像文本、YFCC100M 和 MS-COCO。开源的大规模数据集包括 Laion5B
CLIP 结构
图像嵌入 ($E_I$) ResNet 或 ViT $[n \times d_I]$
文本嵌入 ($E_T$) Transformer LM $[n \times d_T]$
线性投影 ($W_I$, $W_T$) $[d_I \times d_E]$, $[d_T \times d_E]$
分类的温度参数 $t$(类似于 softmax 温度)
相似性的标签 $L$ 通常是单位矩阵 $[n \times n]$
按列(文本)或按行(图像)的交叉熵损失 $CE_{col | row}$
$loss = 0.5 CE_{col}(S_{scaled}, L) + 0.5 CE_{row}(S_{scaled}, L)$
CLIP 编码器细节
- 修改的全局池化:注意力池化
交叉注意力,其中图像特征是 K,V,Q 由一个学习的常量向量(或一组向量)定义。 - ViT(视觉 Transformer):使用图像的小块(矩形部分)作为标记的 Transformer。
- 文本编码器是一个 GPT-2 风格的模型。
CLIP 训练
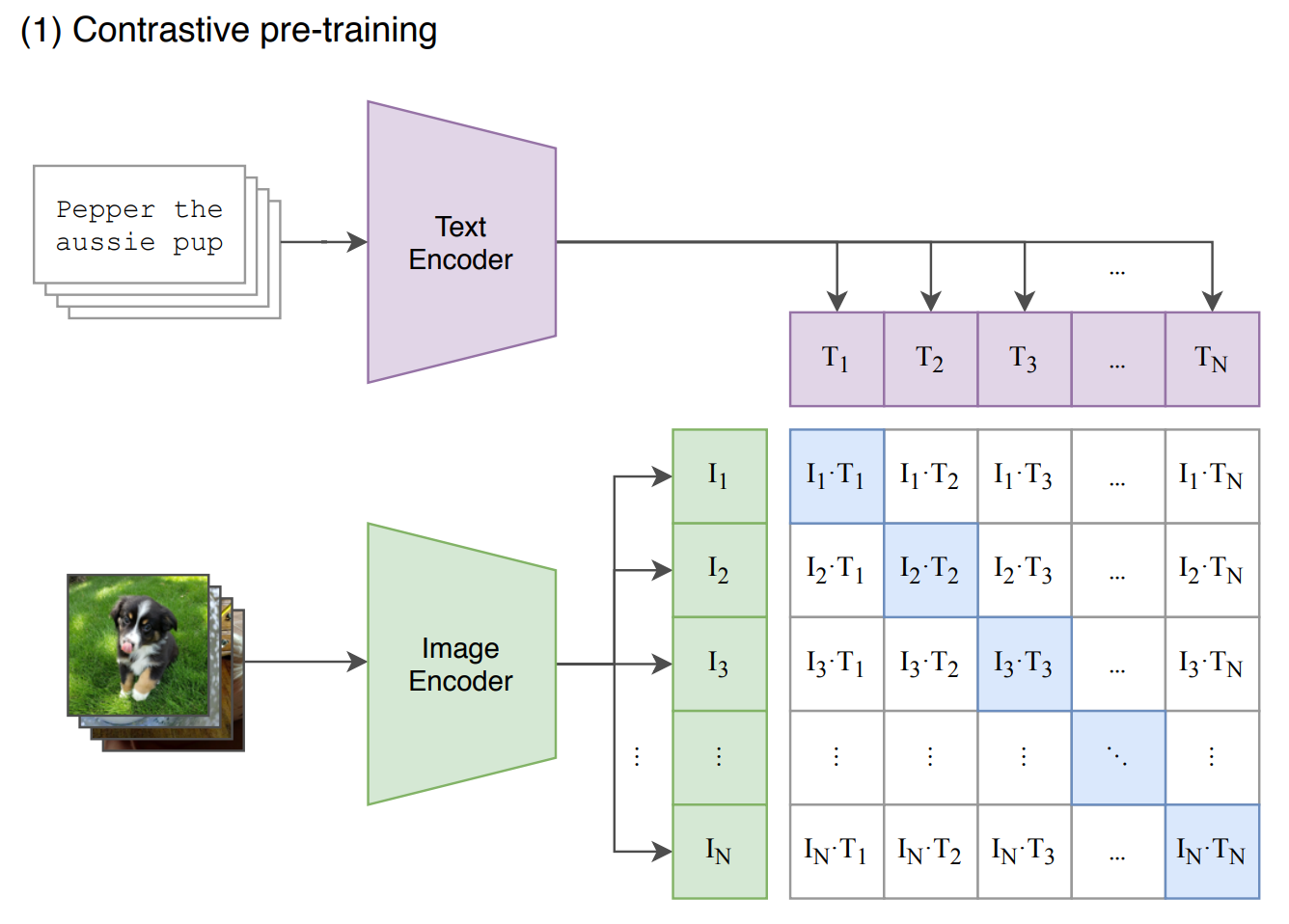
CLIP 零样本推理
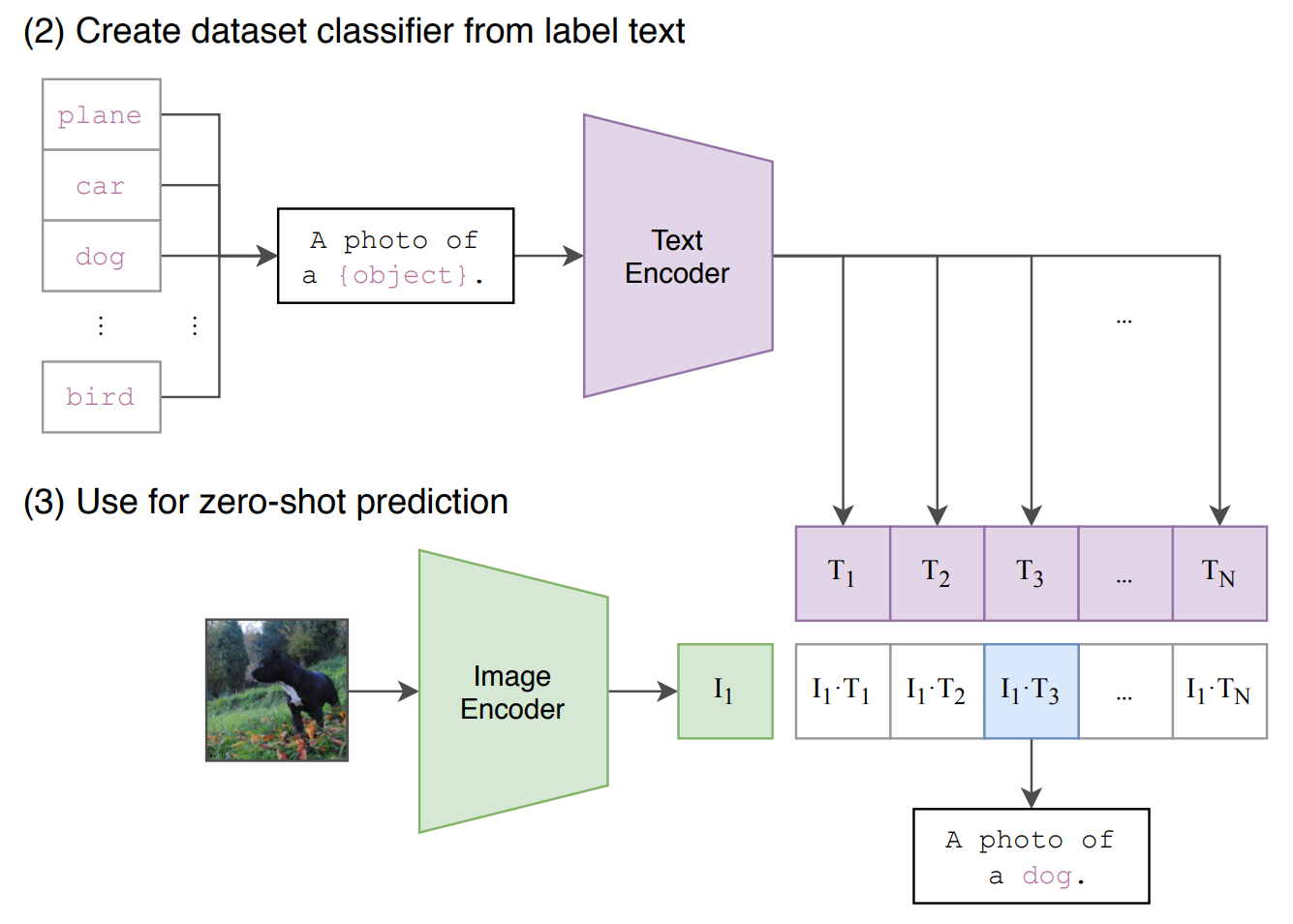
CLIP 可以根据相应的文本定义对图像进行分类。
选择通过找到最相似的类别定义来完成。
其他用例包括:
- 自定义分类器的基础模型
- 迁移学习的基础模型(性能优于以前的 ImageNet 模型)
- 图像检索(搜索引擎)
- 图像生成的条件向量
- 多模态语义
ImageBind
CLIP 展示了通过在一个表示空间中结合多种模态可以产生额外的泛化能力。ImageBind 更进一步,将 $7$ 种模态结合在一个嵌入空间中。

自发 Emergent 对齐
再次使用 InfoNCE,我们可以构建 $(\mathcal{I}, \mathcal{M}_1)$ 和 $(\mathcal{I}, \mathcal{M}_2)$ 的对齐。观察到这种对齐是传递的,并导致部分 $(\mathcal{M}_1, \mathcal{M}_2)$ 对齐。编码器现在从预训练模型(例如:CLIP)初始化。
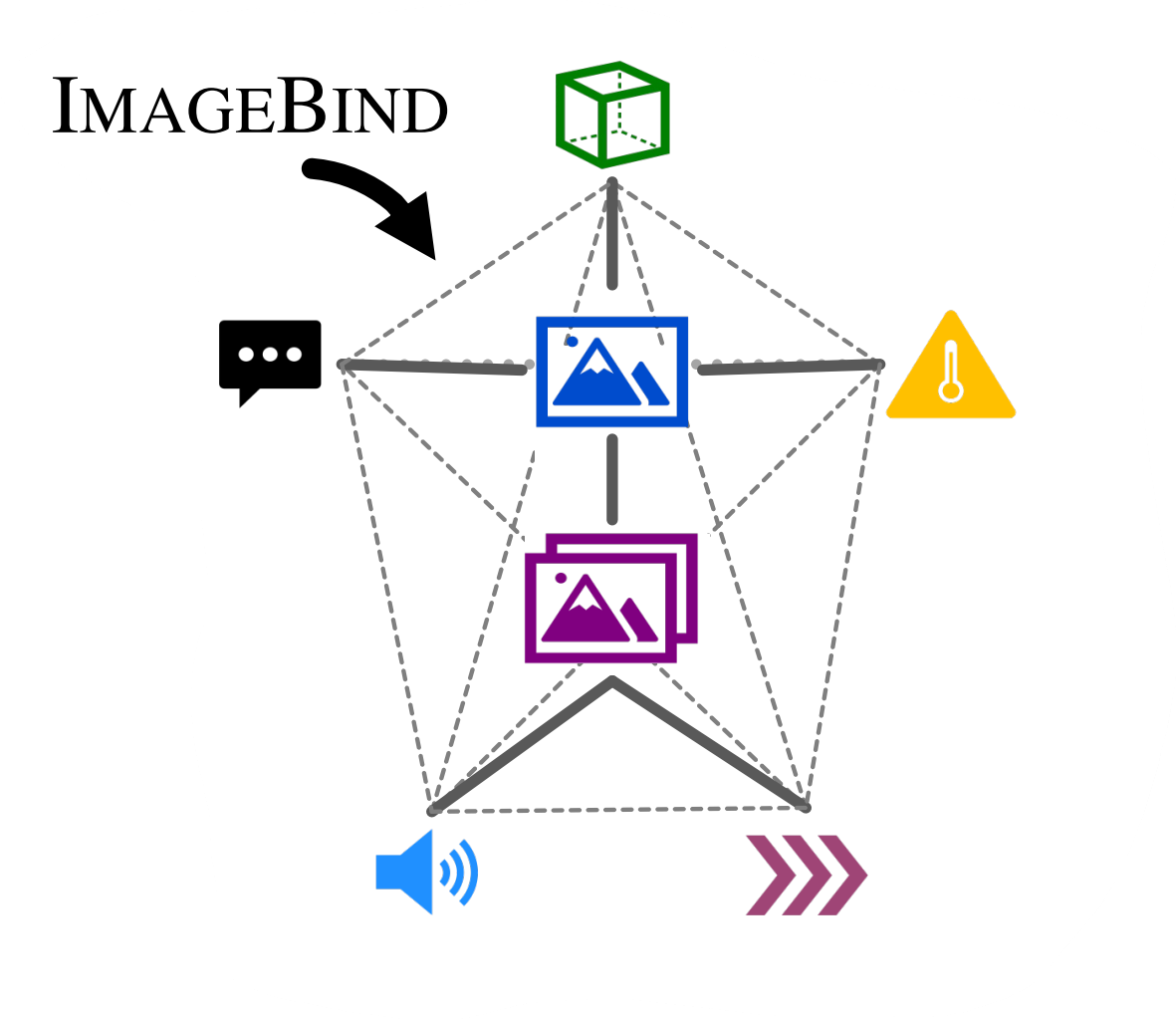
ImageBind 结果
多模态对比嵌入在没有自然存在的多模态信号(例如:文本到音频)的情况下,表现优于监督模态转换器。
ImageBind 的用例示例包括:
- 跨模态检索
- 嵌入空间算术
- 跨模态解码器再利用
跨模态检索


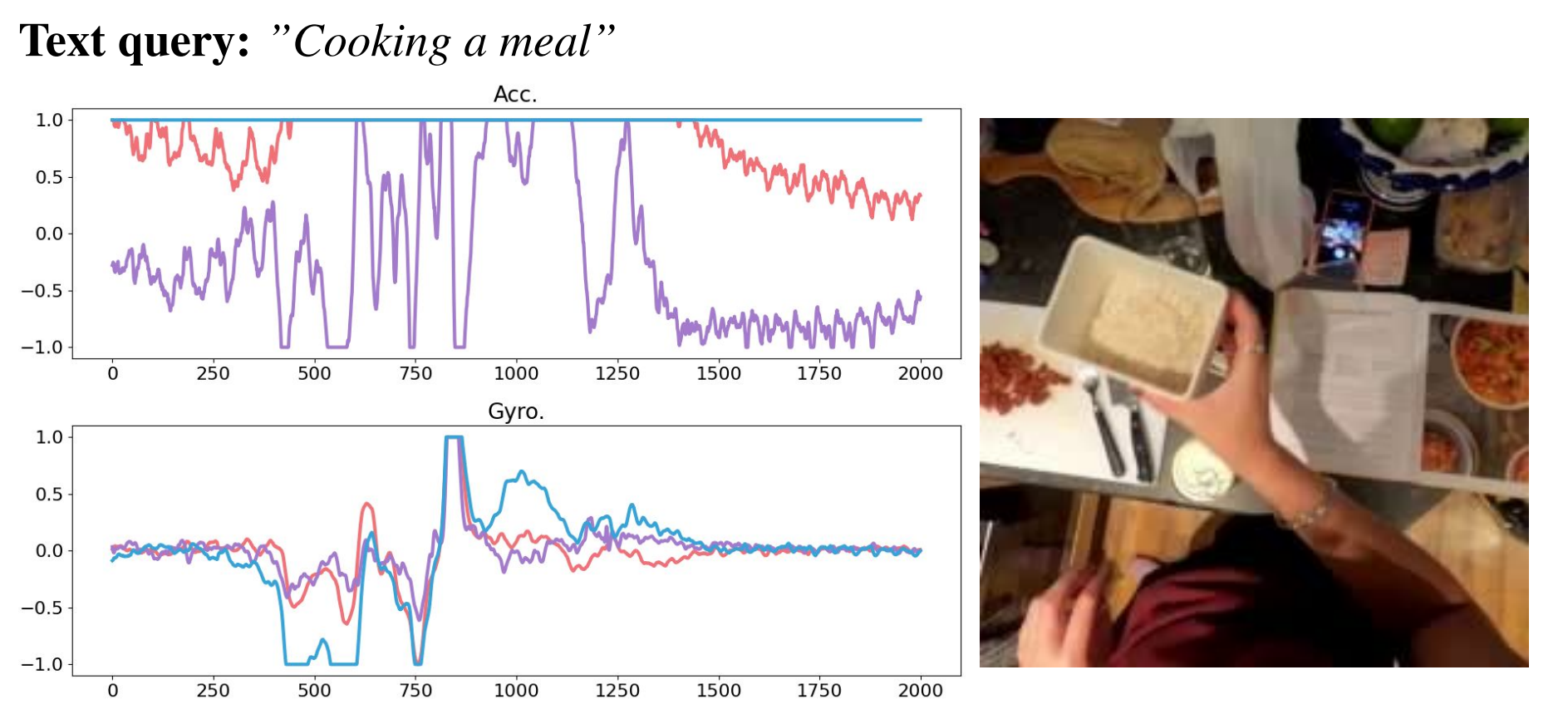
嵌入空间算术

跨模态解码器再利用

解码方法
如何反转联合嵌入?
- 迭代方法
- 前缀解码器
- 零样本解码器
- 对比描述器(Contrastive Captioners CoCa)
- 扩散过程(Diffusion)
我们的示例主要集中在视觉-语言模态对(主要是描述),但这些方法也可以适用于其他模态对。
迭代解码器
最简单的解决方案,不涉及训练。
该方法依赖于语言模型。在生成过程中,中间文本输出被迭代地编码到联合 CLIP 空间,其中与编码图像表示最相似的被选中。然后基于这些生成新的候选描述(或续写)。
问题:
- 不准确(没有适当的指导)
- 效率低(随词汇量/描述长度扩展)
前缀解码器
前缀解码器使用经典的 seq2seq 解码方法。通过结合 CLIP 和 LM(通常是 GPT),所需的数据量减少。
一个小的映射网络足以使 CLIP 图像嵌入空间和 LM 兼容。微调 LM 通常会带来轻微的性能提升。
我们可以想象映射器是一个小的 MLP 或 Transformer,从输入图像 $x^i$ 生成 $[p_1^i, …, p_k^i] = MAP(CLIP(x^i))$ 前缀。
前缀解码器中的映射
为什么需要映射?
- 对比损失不能确保正文本-图像对嵌入的精确匹配
- 领域相关的描述可能需要在嵌入空间中稍微不同的对齐/结构
前缀解码器的训练
模型在带有描述的图像上进行微调。使用以下损失函数:
$L = - \sum_{i=1}^N\sum_{j=1}^M log p_\theta(c_j^i | p_1^i, …, p_k^i, c_1^i, …, c_{j-1}^i)$
其中 $c_1^i, …, c_{j-1}^i$ 是之前的描述标记,$\theta$ 表示可训练参数。
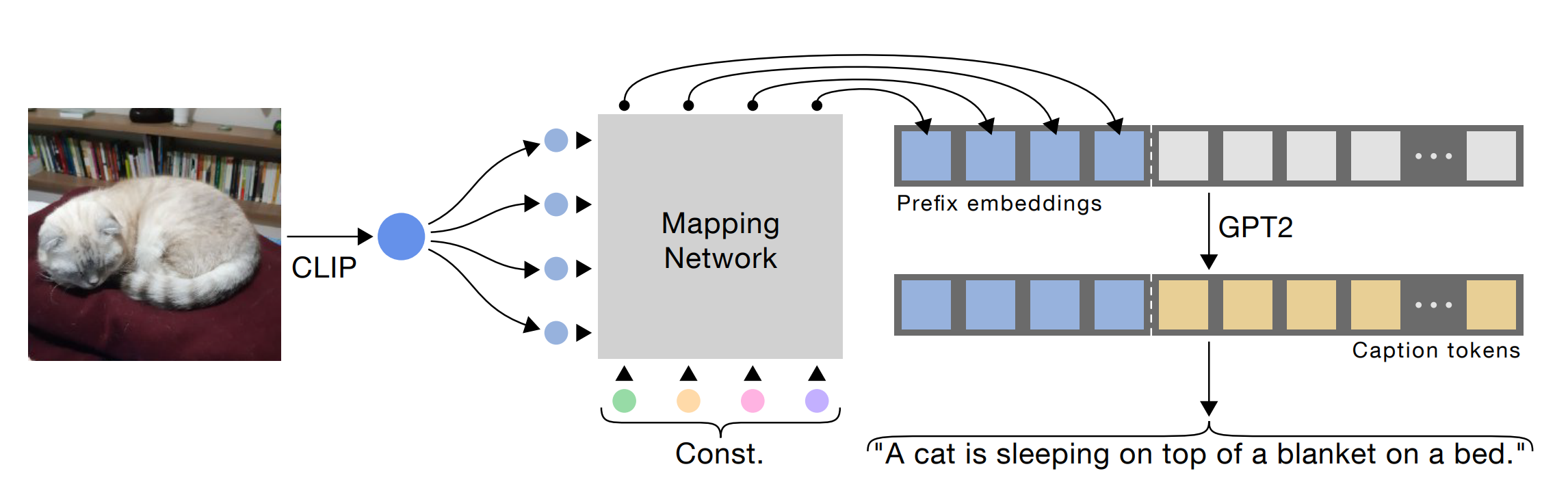
零样本解码器
虽然前缀解码器有效且性能可接受,但它们仍然需要依赖于领域的(图像,标题)训练数据。
最流行的解决方案使用仅文本前缀微调解码器,并使用不同的技巧来替换 CLIP 空间映射:
- 基于先前编码文本嵌入的非训练投影
- 噪声注入以训练一个鲁棒的解码器
DeCap
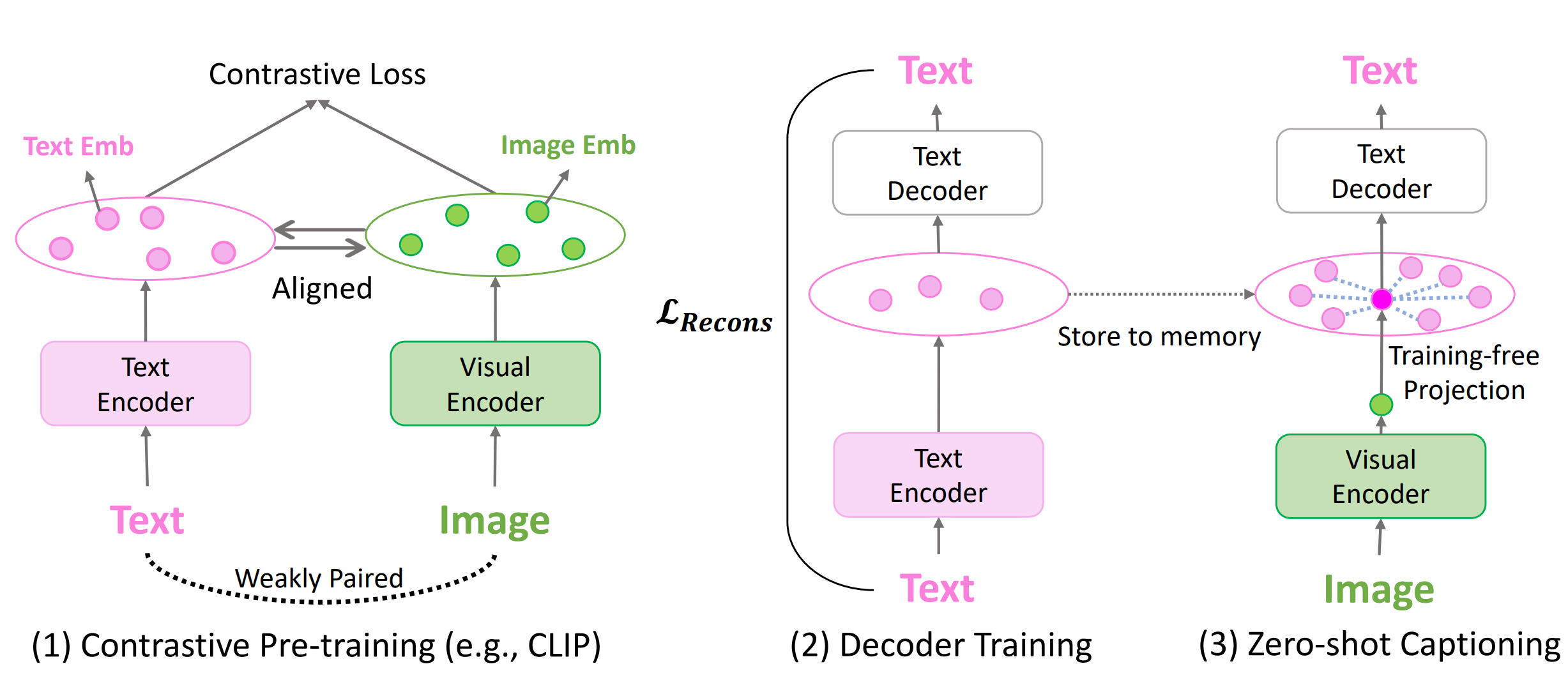
CapDec
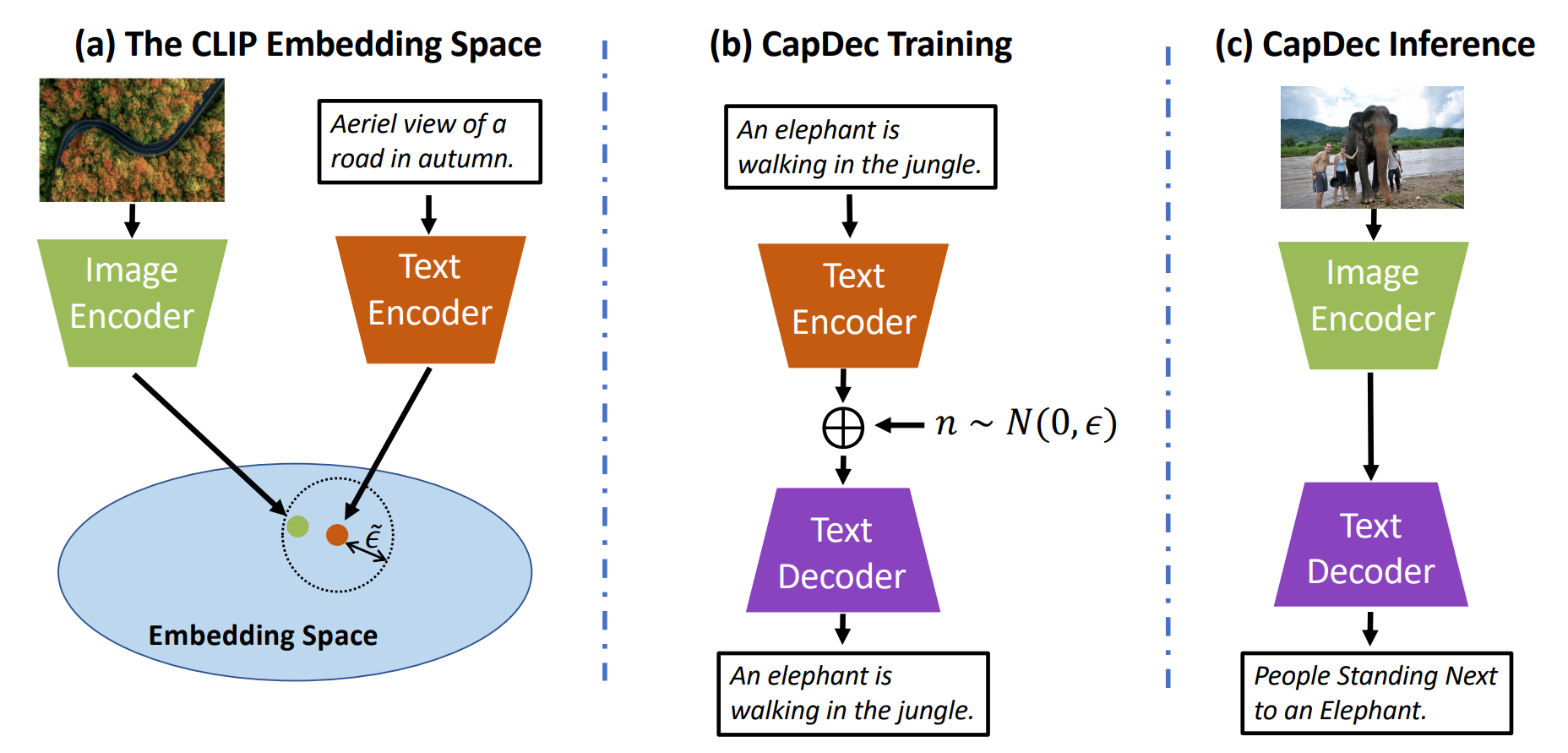
对比描述器(CoCa)
与前缀解码器相关的性能和效率问题:
- 当我们有交叉注意力时,我们还需要前缀吗?
- 为什么不在对比训练阶段并行训练解码器,从而设计一个具有解码能力的原始模型?
- 编码器应该是迁移学习的
CoCa 架构
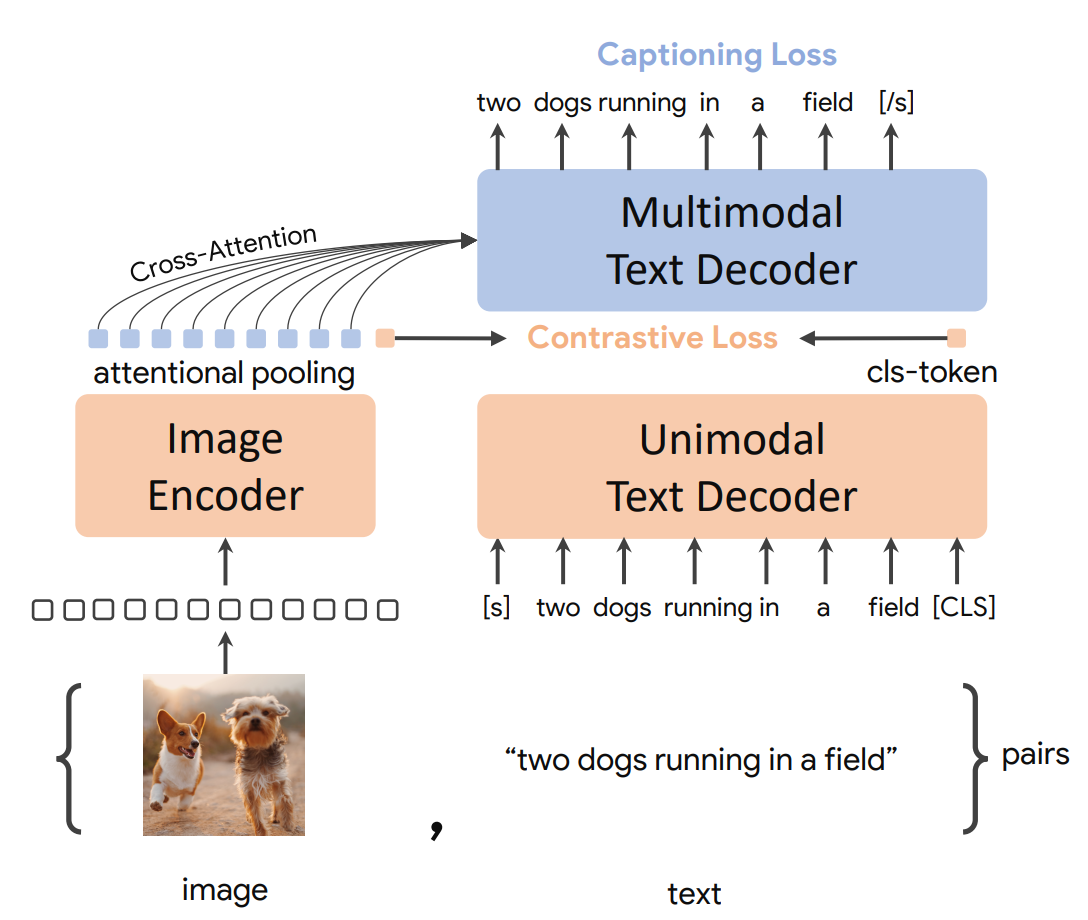
CoCa 训练
- 从单模态预训练模型初始化模型
- 更改视觉头(不同的注意力池化用于标题生成和对比学习)
- 拆分文本,省略前半部分的交叉注意力
- 同时进行对比和重建(标题生成)训练
如果词汇表正好是可能类别的集合,则图像仅数据集也可以用于重建任务。
CoCa 推理
对比描述器模型可以通过进一步微调或以零样本方式使用其构建块的任意组合。CoCa 不仅限于视觉-语言模态。
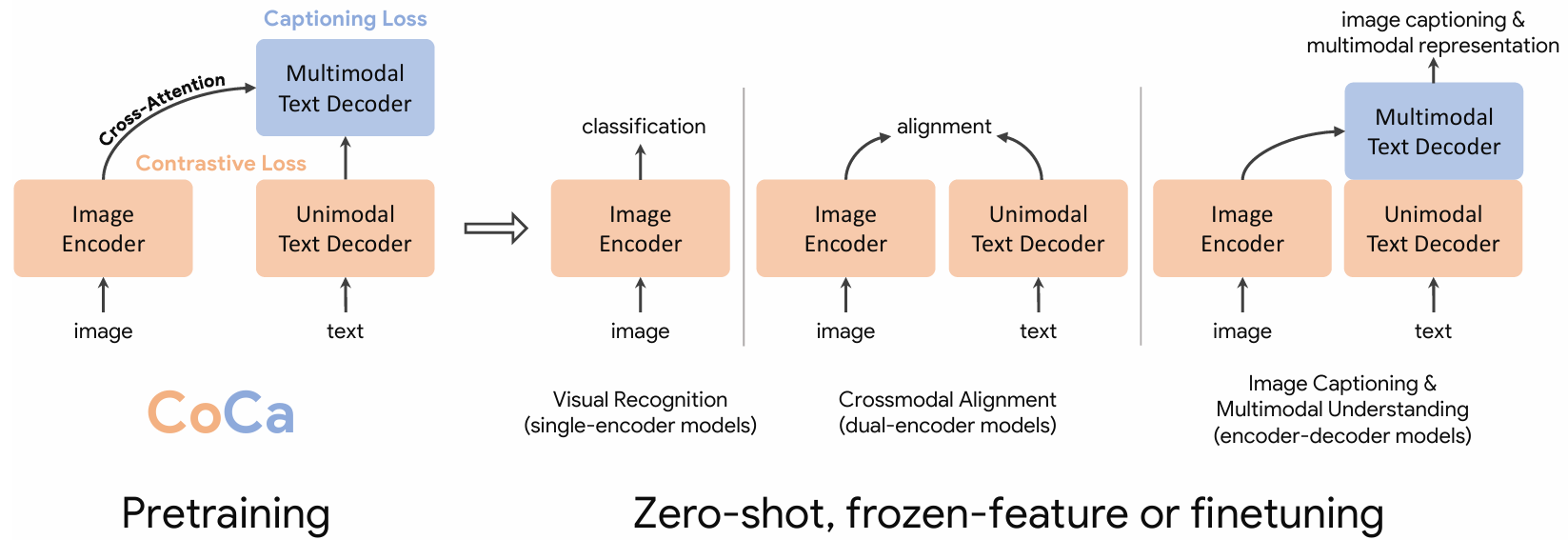
总结
自监督学习(SSL)是一种强大且成本高效的训练方法,可以捕捉给定数据集的潜在分布。广泛使用的神经网络形式是通过对比学习(由 InfoNCE 类损失定义)。
对比方法生成多模态的联合嵌入,通过跨模态对齐创建强大的语义表示。这些方法对于检索和零样本分类任务非常有用。解码器(例如:描述器)也可以构建来执行逆任务。
NLP-Contrastive