3D Computer Vision
我不中了
Basic Estimation Theory
估计 = 给定很多不完美的观测，用数学找“最合理”的未知参数。
| 项目 | 齐次 | 非齐次 |
|---|---|---|
| 方程 | Ax = 0 | Ax = b |
| 目标 | 最小 ‖Ax‖ | 最小 ‖Ax − b‖ |
| 约束 | ‖x‖ = 1 | 无 |
| 解法 | 最小特征值 / SVD | 正规方程 |
| 典型任务 | Homography, F, Plane normal | Line fitting, Calibration |
Solution for homogeneous linear system of equations
齐次线性方程组的解
数学形式 $ A x = 0 $
想象你有很多“约束”，但它们都指向同一个方向。
比如：
- 多个点大致在一条直线上
- 每个点都说一句话：“直线法向量应该满足这个关系”
这些约束合起来就是：
“找到一个非零向量 x，让 Ax 尽量接近 0”
x = 0 永远是解，但没意义
所以我们强制一个约束：
‖x‖ = 1（单位长度）
解：x 是 A 的最小奇异值（Singular value）对应的奇异向量。
典型例子
平面拟合 / 直线拟合
很多 3D 点 ≈ 在一个平面上：$ax + by + cz + d = 0$
→ 对每个点是一条齐次线性方程
→ 堆起来就是 (Ax = 0)
→ 用 最小特征值（Eigenvalue）解
Solution for inhomogeneous linear system of equations
非齐次线性方程组的解
现在不是“全指向 0”，而是：
每个观测点说：“结果应该是 b，但我有噪声”
- 你问 100 个人体重
- 每个人都给你一个“差不多”的数
- 不可能完全一致
核心思想：最小二乘
找一个 x，使 误差平方和最小
$\min_x |Ax - b|^2$
解满足 正规方程（Normal Equation）：
$A^T A x = A^T b$
→ 解为：
$x = (A^T A)^{-1} A^T b$
几何解释
Ax 是所有可能结果的一个子空间
b 被“投影”到这个子空间上
投影点就是最优解
Robust Fitting Methods
最小二乘一遇到离群点（outliers）就会崩。
- 你要用很多点拟合一条直线
- 80% 的点在直线附近
- 20% 是错误匹配（完全乱飞）
普通最小二乘会被这 20% “拉歪”
RANSAC 的思想：
与其相信所有点，不如只相信“彼此一致”的点
RANSAC 的核心思想
随机抽最少点 → 建模型 → 看谁支持它 → 重复 → 选支持最多的模型
The RANSAC method
Step 1：随机采样（Random Sampling）
- 随机选 最小样本数 的点
- 这个数量 = 模型所需的最小点数
例子：
- 直线：2 点
- Homography：4 点
- Fundamental matrix：7 或 8 点
这一步的假设是：
“这一次，抽到的点全是 inliers”
Step 2：模型估计（Model Estimation）
- 用这几个点
- 直接算一个模型（通常是线性解）
例子：
- 2 点 → 一条直线
- 4 对点 → 一个 Homography
Step 3：一致性检测（Consensus / Inlier Test）
- 用这个模型
- 测试所有数据点
- 计算误差（distance / reprojection error）
判断规则：
“误差 < 阈值 → inlier
误差 ≥ 阈值 → outlier”
Step 4：记录支持度（Support）
统计：
有多少 inliers 支持这个模型
支持度 = inlier 数量
Step 5：重复 + 选择最优
- 重复以上步骤 N 次
- 选择 inlier 数最多 的模型
最后一步：
用所有 inliers 再做一次最小二乘精估
这是为什么 RANSAC 的结果不“粗糙”。
RANSAC 是“在参数空间里做投票”
- 每一次随机采样 → 提出一个假设
- 每个数据点 → 给“支持 / 不支持”投票
- 得票最多的模型 → 胜出
最小样本数
- 由模型决定
- 决定了 RANSAC 的“基本成本”
阈值（Threshold）
- 决定 inlier / outlier
- 太小 → 好点被误删
- 太大 → 坏点混进来
要跑多少次才够？
“希望至少有一次，抽到的点全部是 inliers”
优点
- 对 outliers 极其鲁棒
- 简单、通用
- 和任何模型都能搭配
缺点
- 随机 → 结果不完全确定
- 参数（阈值、次数）需要经验
- 只能找到 一个模型
但真实数据里可能有多个模型
Multi-model Fitting
“RANSAC 只能找一个模型，那如果有多个模型怎么办？”
真实世界里，数据往往不只来自一个模型。
典型例子
- 激光雷达点云：地面 + 墙 + 桌面
- 图像直线检测：多条直线
- 特征匹配：多个平面
普通 RANSAC：
- 只能找到 inliers 最多的那一个模型
- 其他结构会被当成 outliers 丢掉
| Sequential RANSAC | MultiRANSAC |
|---|---|
| 找一个，删一个 | 多个一起找 |
| 贪心 | 全局视角 |
| 简单 | 更复杂 |
| 易错 | 更稳健 |
Sequential RANSAC
一次只找一个模型，找到后把它删掉，再找下一个
Step 1：在全部数据上跑 RANSAC
- 得到 模型 M₁
- 得到它的 inliers 集合 I₁
Step 2：移除 inliers
- 从数据集中删除 I₁
- 剩下的点 ≈ 其他模型 + 噪声
Step 3：在剩余数据上再跑 RANSAC
- 得到 模型 M₂
- 得到 inliers I₂
Step 4：重复
直到：
- 剩余点太少
- 或者 RANSAC 再也找不到“足够支持”的模型
形象比喻
像剥洋葱
一层一层剥
每一层都是一个模型
典型应用
- 多条直线检测
- 多个平面（尤其是 LiDAR / depth 数据）
优点
- 非常简单
- 基于标准 RANSAC
- 容易实现、调试
致命缺点
贪心（greedy）算法
具体问题：
- 第一个模型如果估计得不好
- 错误的 inliers 被删掉
→ 后面的模型永远找不到
MultiRANSAC
同时寻找多个模型，而不是一个一个删。
RANSAC 不再只维护一个“最佳模型”，
而是维护 多个候选模型，
数据点可以在模型之间“竞争归属”。
大量随机采样
生成许多模型假设
每个点计算：
- 它对每个模型的误差
点被分配给：
- 误差最小的模型
对每个模型：
- 用自己的 inliers 重新估计
迭代直到稳定
本质类似：clustering + RANSAC
优点
- 不容易被早期错误带偏
- 能处理 模型重叠
- 适合复杂场景
缺点
- 算法复杂
- 参数多
- 计算量大
- 实现难度高
什么时候用 Sequential RANSAC？
当模型之间分离得比较清楚
什么时候用 MultiRANSAC？
模型数量未知
或多个模型规模接近
或模型有重叠
Camera Models
相机模型描述的是：3D 点如何变成 2D 像素。
核心变量只有三个：
- 投影方式
- 是否考虑深度变化
- 自由度多少
Perspective camera
透视 / 针孔相机
离相机近的物体看起来大，远的看起来小。
几何直觉
- 所有光线经过一个点（焦点）
- 3D 点 → 沿射线投影到成像平面
$u \sim K ,[R \mid t], X$
含义：
- $X$：世界坐标里的 3D 点
- $R,t$：相机姿态
- $K$：内参（焦距、主点等）
齐次坐标，只有比例意义
核心特性
- 有尺度歧义（scale ambiguity）
- 深度 $Z$ 决定成像大小：
$u \propto \frac{1}{Z}$
优点
- 最真实
- 精确描述真实相机
- 所有 3D 几何理论的基础
缺点
- 参数多（内参 + 外参）
- 非线性
- 数学处理复杂
什么时候用？
近距离 / 大景深变化 / 精确 3D 重建
Orthogonal projection
正交投影
所有点“垂直”投影到图像平面，不考虑深度。
像工程制图
或影子在正午阳光下
数学直觉
$u = R_{1:2} X + t$
- 只保留 X、Y
- Z 完全被忽略
核心特性
- 没有透视效应
- 远近大小完全一样
- 模型最简单
自由度
5 DoF
- 3（旋转）
- 2（平移）
什么时候用？
物体非常远、深度变化极小
例如：
- 卫星影像
- 极远距离拍摄
Weak-perspective camera
弱透视相机
真实透视太复杂，正交又太粗糙。
折中方案：Weak-Perspective
核心假设
物体深度变化 ≪ 相机到物体的平均距离
换句话说：
- 所有点的 Z 几乎一样
投影思想
- 先 正交投影
- 再整体 缩放
数学直觉
$u = s \cdot R_{1:2}(X - t)$
- (s)：统一尺度因子
- 不再随每个点的 Z 变化
| 特性 | 透视 | 弱透视 | 正交 |
|---|---|---|---|
| 透视缩放 | ✔ | ✔（统一） | ✘ |
| 深度变化 | ✔ | ✘ | ✘ |
| 非线性 | ✔ | ✘ | ✘ |
| DoF | 多 | 6 | 5 |
弱透视 = 缩放正交投影
优点
- 线性
- 无尺度歧义
- 易估计
- 闭式解多
缺点
- 近距离或深度变化大时不准
什么时候用？
人脸、人体、刚体 > 中远距离、相对平坦结构
Tomasi–Kanade 因式分解就是用它
为什么 Tomasi–Kanade 不能用透视？
因为透视投影是非线性的，
而因式分解需要线性模型。
什么时候弱透视会失败？
当物体离相机很近，
或深度变化很大时。
Calibration of Perspective Camera Using a Spatial Calibration Object
给我一些已知 3D 点及其在图像中的位置，我可以估计整个相机。
什么是 Spatial Calibration Object？
- 一个 几何结构已知的 3D 物体
- 上面有 容易检测的特征点
典型例子
- 标定立方体
- 标定板（3D 坐标已知）
- 标定框架
与棋盘的区别：
- 这是 3D 物体
- 棋盘是 平面（2D）
Estimation of projection matrix
投影矩阵 P 的估计
透视相机模型：
$u \sim P X$
其中：
- $X = [X, Y, Z, 1]^T$（3D 点）
- $u = [u, v, 1]^T$（像素）
- $P$：3×4 投影矩阵
P 里有什么？
$P = K , R , [I \mid -t]$
所以：
- K：相机内参
- R, t：相机外参
估计 P = 一步到位估计 整个相机
核心思想
投影矩阵估计是一个“齐次线性问题”
从一个 3D–2D 点对能得到什么？
对一个点：
$u \sim PX$
展开后可以得到：
- 2 条独立线性方程
- 未知量是 P 的 12 个元素（但有尺度歧义）
最少需要多少点？
- P 有 11 个自由度（12 个数 − scale）
- 每个点给 2 个方程
至少需要 6 个 3D–2D 点对
线性估计流程
Step 1：建立线性方程
- 对每个点写出 2 条方程
- 堆叠成：
$A p = 0$
其中：
- $p$：P 的 12 个元素组成的向量
Step 2：解齐次线性系统
- 排除平凡解 $p=0$
- 加约束：$|p| = 1$
解法：
SVD，取最小奇异值对应的向量
Step 3：得到投影矩阵 P
- 只在比例意义下成立
- 已经能把 3D 点投影到图像上
这是代数误差最小化，不是几何误差
所以：
- 通常作为 初值
- 后面可用 非线性优化（Bundle Adjustment）精化
Decomposition of projection matrix
投影矩阵的分解
为什么要分解？
P 本身不好解释，我想要真正的相机参数。
也就是：
- 焦距是多少？
- 主点在哪？
- 相机姿态是什么？
P 的结构再强调一次
$P = K [R \mid t]$
其中：
- 左边 3×3 是 $KR$
- 最后一列与 $t$ 有关
分解的目标
从已知的 P，求：
- K（内参）
- R（旋转）
- t（平移）
核心技术：RQ 分解
为什么不是 QR？
- QR：正交 × 上三角
- 我们需要：上三角 × 正交
所以用 RQ decomposition
分解步骤
Step 1：取 P 的左 3×3 子矩阵
$M = P_{3\times3} = K R$
Step 2：对 M 做 RQ 分解
$M = K R$
- K：上三角矩阵（内参）
- R：正交矩阵（旋转）
需要处理符号，使：
- 焦距为正
- det(R) = 1
Step 3：计算平移向量 t
利用：
$p_4 = -K R t$
解得：
$t = - R^T K^{-1} p_4$
得到的结果
K：
- 焦距
- 主点
- 像素比例
R, t：
- 相机在世界坐标中的姿态
为什么投影矩阵只能估计到比例？
因为使用的是齐次坐标，
缩放 P 不改变投影结果。
为什么需要很多点？
为了抵抗噪声，
实际是一个过定约束问题。
这和棋盘标定有什么区别？
空间标定物是 3D，
棋盘是平面（2D），
棋盘通过多视角间接恢复 3D 信息。
Chessboard-based Calibration of Perspective Cameras
不用 3D 标定物，只用一块平面棋盘，通过多张不同姿态的图片来标定相机。
为什么棋盘能标定相机？
关键原因
- 棋盘是 平面
- 平面 ↔ 图像之间存在 Homography
- 多个不同姿态 ⇒ 多个 Homography
- 这些 Homography 共享同一个相机内参 K
Chessboard-based Calibration 的整体流程（口语标准版）
Step 1：拍摄多张棋盘图像
- 同一块棋盘
- 不同位置 + 不同倾斜角度
- 至少 3 张，实际更多更稳
Step 2：检测棋盘角点
- 棋盘角点位置精确、结构规则
- 可做到 亚像素精度
Step 3：对每一张图像估计 Homography
- 棋盘在世界坐标中是一个平面
- 每张图像：
$u \sim H X_{\text{plane}}$
Step 4：由多个 Homography 解相机内参 K
利用：
- 旋转矩阵列向量正交
- 单位长度约束
得到 K（焦距、主点等）
Step 5：加入畸变模型并非线性优化
同时优化：
- K
- 外参
- 畸变参数
最小化 重投影误差
为什么要考虑畸变？
真实镜头不是理想针孔模型。
理想情况：
- 直线 → 图像中仍是直线
现实情况：
- 直线 → 弯曲
这会严重影响 3D 重建精度
Radial distortion
径向畸变
离图像中心越远，偏移越严重。
常见两种类型
Barrel distortion（桶形）
- 直线向外鼓
- 最常见
- 广角镜头
Pincushion distortion（枕形）
- 直线向内凹
- 长焦镜头
数学模型
以主点为中心
位移大小是：
- 距离 r 的函数
用多项式近似：
- (k_1, k_2, k_3)
“用 r²、r⁴、r⁶ 的多项式修正”
重要细节
通常假设：
- 畸变中心 ≈ 主点
参数很小
在 非线性优化阶段一起估计
Tangential distortion
产生原因
镜头与成像平面没有完全对齐。
也就是：
- 透镜装歪了
- 光轴不完全垂直传感器
直观表现
- 点被“拉向一侧”
- 不再是纯粹的径向对称
数学特性
与：
- x·y
- x²、y²
相关
参数通常是：
- $p_1, p_2$
与径向畸变的关系
切向畸变不是径向畸变的替代，而是补充。
- Radial：对称
- Tangential：非对称
两种畸变的对比
| 项目 | Radial | Tangential |
|---|---|---|
| 原因 | 镜头曲率 | 镜头未对齐 |
| 对称性 | 中心对称 | 非对称 |
| 常见程度 | 非常常见 | 较少 |
| 参数 | k₁,k₂,k₃ | p₁,p₂ |
为什么畸变参数要用非线性优化？
畸变模型是非线性的，线性方法解不了。
所以流程是：
先忽略畸变，线性估计 K
再：
- 加入畸变
- 用 Levenberg–Marquardt
- 最小化重投影误差
为什么要拍不同姿态？
否则约束不足，
内参解不唯一。
畸变在什么时候最明显？
图像边缘。
棋盘标定 = 多张平面 Homography → 解内参 → 加畸变 → 非线性精化
Plane-plane Homography
平面—平面单应变换
如果所有点都在同一个平面上，那么两张图之间只需要一个 3×3 矩阵就能互相变换。
一般情况：
- 3D 点 → 两张图
- 需要 深度 Z
- 问题复杂
但如果：
所有点都在同一个平面上
那么：
- 深度被“消掉”
- 投影关系变成 2D ↔ 2D
所以可以用 Homography
数学形式
$u’ \sim H u$
- $u, u’$：两张图里的像素点（齐次坐标）
- $H$：3×3 非奇异矩阵
- “$(\sim)$”：比例意义
Homography 的自由度
- 9 个元素
- 1 个尺度不重要
8 个自由度
Homography 从哪来？
场景 1：平面物体 + 两个相机
- 相机 1：$P_1$
- 相机 2：$P_2$
- 物体在同一平面上
消去 3D 坐标得到：
图像 1 ↔ 图像 2 的 Homography
场景 2：同一个相机，旋转但不平移
- 相机光心不变
- 只旋转
整个场景都满足 Homography
这是全景拼接的核心前提
几何性质
- 直线 → 直线
- 平行线 不一定保持平行
- 角度、长度 不保持
Homography 是 投影变换
Panoramic images by homographies
用单应性生成全景图
全景图的核心假设
相机只旋转，不平移。
为什么？
- 平移 → 不同深度点产生视差
- 视差 → 一个 Homography 对不上
全景拼接的几何原理
关键公式
$u’ \sim K R_2 R_1^T K^{-1} u$
意思：
- 同一相机
- 不同朝向
- 只靠旋转矩阵关系
这就是 Homography
全景拼接的标准流程
Step 1：特征点检测
- SIFT / ORB / SURF
Step 2：特征匹配
- 最近邻匹配
- 有大量错误匹配
Step 3：RANSAC 估计 Homography
- 剔除错误匹配
- 得到稳定的 H
Step 4：图像 Warp
- 用 H 把一张图“扭”到另一张图坐标系
Step 5：图像融合
重叠区域：
- 平均
- 加权
- 多带融合
为什么全景拼接要用 RANSAC？
因为特征匹配里一定有大量 outliers。
什么时候 Homography 不适合？
重要反例
- 相机有明显平移
- 场景是 强 3D
- 近处物体明显
会出现：
- 重影
- 拉伸
- 错位
Homography 的两个经典应用
图像拼接（Panorama）
- 手机全景
- 建筑内部
平面校正（IPM）
- 路面矫正
- 俯视图
- 车道线检测
Homography 和 Fundamental Matrix 的区别？
Homography 假设 点在同一平面
Fundamental Matrix 适用于 一般 3D 场景
全景拼接失败的原因？
相机发生平移
或场景不是单一深度
一句话总结
Homography 是平面之间的投影关系，
在相机纯旋转时可用于整幅图像的对齐。
Estimation of Homography
单应矩阵的估计
给定两张图像中的点对应关系，估计 Homography 矩阵 H。
已知：
- 点对应：
$u_i \leftrightarrow u’_i$
假设：
- 所有点 在同一个平面上
- 或相机 纯旋转
目标：
$u’_i \sim H u_i$
Homography 的未知量
- H 是 3×3 矩阵
- 有 8 个自由度（尺度无关）
所以：
至少需要 4 对点
（4 × 2 = 8 个独立约束）
从“一对点”能得到什么？
设：
$u = [x, y, 1]^T,\quad u’ = [x’, y’, 1]^T$
由：
$u’ \sim H u$
展开后可以得到：
- 2 条独立线性方程
- 对 H 的元素是线性的
线性方程组的形式
对每个点对：
- 写成：
$A_i h = 0$
其中：
- $h$：H 的 9 个元素组成的向量
所有点堆起来：
$A h = 0$
这是一个齐次线性系统
如何解这个齐次系统？
- 平凡解 $h=0$ 没意义
- 加约束：
$|h| = 1$
转化为：
最小化 (|Ah|)，同时 (|h|=1)
解法
对矩阵 A 做 SVD，取最小奇异值对应的向量。
原因：
- 这是 代数误差最小化
- 数值稳定
- 和前面学的 estimation theory 完全一致
你已经用 SVD 解了，为什么还不行？
数值不稳定。
原因：
- 像素坐标数值大（几百上千）
- A 中不同列的量级差很多
- SVD 对尺度非常敏感
Data Normalization
在解 Homography 之前，先把点坐标“变得好看”。
对 每一张图像的点集，分别做归一化：
Step 1：平移（Translation）
- 把点集的 质心 移到原点
Step 2：缩放（Scaling）
缩放，使：
- 点到原点的 平均距离 = √2
Step 3：得到归一化变换矩阵 T
$u’ = T u$
用归一化点来估计 Homography
- 用归一化后的点：
$\tilde{u}’ \sim \tilde{H} \tilde{u}$ - 解：
$\tilde{A} \tilde{h} = 0$
得到的是 归一化坐标系下的 Homography
反归一化
最终结果不是 $\tilde{H}$，而是：
$H = T_2^{-1} \tilde{H} T_1$
其中：
- $T_1$：第一张图的归一化矩阵
- $T_2$：第二张图的归一化矩阵
没有归一化的 8-point / 4-point 方法在实践中几乎不可用。
Hartley 证明过：
- Normalization 是“必须的，不是可选的”
优点
- 快
- 有闭式解
- 适合作为初值
缺点
- 只最小化 代数误差
- 不是真正的几何距离
- 对 outliers 极度敏感
所以：
- RANSAC + 非线性优化 通常一起用
为什么平均距离是 √2？
为了让坐标尺度在 1 的量级，
提高数值稳定性。
归一化对结果有影响吗？
不改变几何关系，
但显著提升数值精度。
如果点很多怎么办？
问题变成过定约束，
SVD 自动给出最小二乘意义下的解。
Homography 估计 = 线性齐次系统 + SVD + 数据归一化 + 反归一化
Basics of Epipolar Geometry
极几何基础
极几何描述的是：一个 3D 点在两张图像中的对应关系。
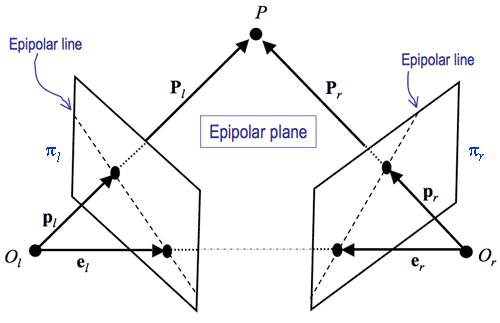
为什么需要 Epipolar Geometry？
- 两张图像
- 一个 3D 点 X
- 在两张图里各有一个像素位置
问题：
第二张图里，对应点到底在哪？
Epipolar Geometry 的核心直觉
三个关键元素
Baseline
- 连接两个相机光心的直线
Epipolar plane（极平面）
由：
- 3D 点 X
- 两个相机光心
共同确定的平面
Epipolar lines（极线）
- 极平面与图像平面的交线
一个点在第一张图像中确定后，
它在第二张图像中一定落在一条极线上。
搜索问题：
- 从 2D 区域搜索
- 降到 1D 直线搜索
Epipolar Constraint（极约束）
对应点必须满足极约束，否则不可能来自同一个 3D 点。
$u_2^T F u_1 = 0$
Essential matrix
本质矩阵
Essential Matrix 什么时候用？
当相机是“已标定”的。
也就是说：
- 内参 (K_1, K_2) 已知
- 像素点已转换成 归一化相机坐标
Essential Matrix 的定义
$u_2^T E u_1 = 0$
其中：
$E = [t]_\times R$
含义：
- $R$：相机之间的旋转
- $t$：相机之间的平移方向（只有方向，没有尺度）
Essential Matrix 的关键性质
5 个自由度
- 3（旋转）
- 2（平移方向，尺度未知）
秩为 2
两个非零奇异值相等
可以通过 SVD 分解得到 R 和 t
- 有 4 种解
- 只有一个是物理正确的
Essential Matrix 在做什么？
它把“几何关系”编码成一个矩阵。
- 不关心像素单位
- 只关心空间结构
Fundamental matrix
基础矩阵
Fundamental Matrix 什么时候用？
当相机“未标定”时。
也就是：
- 焦距未知
- 主点未知
- 像素坐标是原始的
Fundamental Matrix 的定义
$u_2^T F u_1 = 0$
和 E 形式一样，但：
$F = K_2^{-T} E K_1^{-1}$
F = E + 相机内参的影响
Fundamental Matrix 的性质
- 7 个自由度
- 秩为 2
- 定义在像素坐标系
- 完全描述两幅图之间的极几何
E vs F 的核心区别（一定要会对比）
| 项目 | Essential (E) | Fundamental (F) |
|---|---|---|
| 是否需要标定 | ✔ | ✘ |
| 坐标 | 归一化相机坐标 | 像素坐标 |
| 自由度 | 5 | 7 |
| 是否可分解 | ✔（R,t） | ✘（直接） |
E 是“纯几何”，F 是“几何 + 相机内参”。
Rectification
立体校正
为什么要 Rectification？
为了让立体匹配更简单。
原始情况：
- 极线是任意方向
- 搜索对应点很麻烦
Rectification 的目标（必说）
把两张图像变换，使对应点落在同一行。
也就是说：
- 极线 → 水平线
- epipoles → 无穷远
Rectification 在几何上做了什么？
- 对两张图像分别应用 Homography
- Homography 是由 极几何（F 或 E） 决定的
不需要知道 3D 结构
只需要知道 F
Rectification 的好处
- 2D 搜索 → 1D 搜索
- 立体匹配更快
- 深度计算更稳定
Rectification 的代价
图像会被扭曲。
特别是：
- Wide-baseline stereo
- 大视角差
所以：
- 有时 不做 rectification
- 而是直接沿极线搜索
Rectification 是否必须？
不必须，但通常有利于匹配。
Rectification 和 Homography 有什么关系？
Rectification 本质上是
用 Homography 把极线对齐。
如果相机已标定，用 E 还是 F？
用 E 更好，但 F 也可以。
极几何把点匹配从 2D 搜索变成 1D 搜索，
E 和 F 分别描述标定和未标定情况下的这种约束。
Estimation of Essential and Fundamental Matrices
本质矩阵 E 与基础矩阵 F 的估计
从两张图像的点对应关系中，估计描述它们极几何关系的矩阵。
已知：
- 点对应：
$u_{1i} \leftrightarrow u_{2i}$
目标：
- 未标定相机 → Fundamental matrix F
- 已标定相机 → Essential matrix E
共同约束（极约束）：
$u_2^T F u_1 = 0 \quad \text{或} \quad u_2^T E u_1 = 0$
从“一对点”能得到什么？
对每一对对应点：
- 可以写出 1 条线性方程
- 对矩阵元素是线性的
把 N 对点堆起来：
$A f = 0 \quad \text{或} \quad A e = 0$
这是一个齐次线性系统
最少需要多少点？
Fundamental matrix F
- 自由度：7
- 实践中：
8-point method（≥8 点）
Essential matrix E
- 自由度：5
- 理论最少：5 点
- 实践中常用：
8 点法 + 约束
线性估计的标准步骤
Step 1：建立线性系统
- 对每对点写：
$u_2^T F u_1 = 0$ - 得到：
$A f = 0$
Step 2：SVD 解齐次系统
- 排除平凡解
- 加约束：
$|f| = 1$
解法：
SVD，取最小奇异值对应向量
Step 3：强制秩约束
理论要求：
- rank(F) = 2
- rank(E) = 2
做法：
- 对估计矩阵做 SVD
- 把最小奇异值设为 0
- 重构矩阵
直接用 8-point method 行不行？
数值不稳定，必须归一化。
Data normalization
为什么要 Data Normalization？
像素坐标量级太大，导致线性系统病态。
影响：
- SVD 不稳定
- 结果对噪声极度敏感
归一化做了什么？（和 Homography 一样）
对 两张图的点，分别独立归一化：
Step 1：平移
- 点集质心 → 原点
Step 2：缩放
- 平均距离 → √2
Step 3：得到归一化矩阵
$\tilde{u} = T u$
完整流程
- 原始点 → 归一化点
- 用归一化点估计 $\tilde{F}$ 或 $\tilde{E}$
- 强制秩约束
- 反归一化：
$F = T_2^{-T} \tilde{F} T_1^{-1}$
对 E 也是同理
为什么归一化是“必须的”？
没有归一化的 8-point 方法在实践中几乎不可用。
这是 Hartley 的经典结论。
Decomposition of essential matrix
本质矩阵的分解
为什么要分解 E
E 只是约束，我真正想要的是相机的 R 和 t。
Essential Matrix 的结构回顾
$E = [t]_\times R$
性质：
- rank = 2
- 两个非零奇异值相等
分解方法
Step 1：对 E 做 SVD
$E = U , \text{diag}(\sigma, \sigma, 0) , V^T$
Step 2：构造候选解
利用固定矩阵 (W) 和 (Z)，得到：
- 2 个旋转
- 2 个平移方向
总共 4 种 (R, t) 组合
为什么有 4 种解？
- 平移方向有正负
- 旋转有对称解
如何选正确解？
正深度约束（cheirality condition）
也就是：
- 3D 点必须在 两个相机前方
只有 1 种解满足
分解后的结果意味着什么？
得到：
- R（准确）
- t（只有方向，没有尺度）
这是为什么：
- 单目 / 双目视觉 无法恢复绝对尺度
为什么 E 不能直接用最小二乘？
因为 E 有额外的结构约束，
必须强制秩和奇异值条件。
E 和 F 的估计流程有何不同？
流程几乎一样，
区别在于：
- E 用归一化相机坐标
- F 用像素坐标
为什么实际中常用 RANSAC？
因为点对应中一定有 outliers，
线性方法对 outliers 非常敏感。
E/F 的估计 = 归一化 + 线性 SVD + 秩约束，
E 还能进一步分解出相机的相对位姿。
Triangulation
从两张图像恢复 3D 点
三角化就是：用两台相机看到同一个点的位置，反推出这个点在 3D 空间中的位置。
Triangulation 在整个流程中的位置
特征匹配 →
RANSAC 估计 E/F →
分解得到 R, t →
Triangulation 得到 3D 点
Triangulation 的几何直觉
图像中的一个像素，对应空间中的一条射线。
相机光心 + 像素 → 一条 3D 射线
两台相机 → 两条射线
理想情况：
- 两条射线相交于一个点
实际情况（有噪声）：
- 两条射线 不严格相交
所以问题变成：
找一个点，使它到两条射线的距离最小
Standard stereo vision
标准立体视觉
什么是 Standard Stereo？
相机已经标定，并且经过了 Rectification。
也就是说：
两个相机：
- 光轴平行
- 图像行对齐
极线是 水平线
Standard Stereo 的最大简化
对应点只在同一行上。
因此：
- 不用 2D 搜索
- 只用 1D 搜索（沿行）
Disparity（视差）核心概念
$d = x_L - x_R$
- 左右图中同一行的横向差
关键关系
视差越大，点越近；
视差越小，点越远。
深度公式
$Z = \frac{f \cdot B}{d}$
- $f$：焦距
- $B$：基线长度
- $d$：视差
这是 标准立体 最重要的结果
Standard Stereo 的优缺点
优点
- 非常快
- 实现简单
- 工程上极其常用
缺点
- 需要精确标定
- 需要 rectification
- 只适合规则双目系统
General stereo vision
一般立体视觉
为什么需要 General Stereo？
现实中，相机不一定是规则摆放的。
例如：
- 相机姿态任意
- 非平行光轴
- 多视角重建
General Stereo 的输入
已知：
- 相机投影矩阵：
$P_1, P_2$ - 对应点：
$u_1 \leftrightarrow u_2$
目标：
- 恢复 3D 点 (X)
General Triangulation 的本质
每个像素定义一条射线，
我们找一个 3D 点，使它到所有射线的重投影误差最小。
常见解法
方法 1：线性三角化
- 用：
$u \times (PX) = 0$ - 得到：
$A X = 0$ - 用 SVD 解齐次系统
快，但不是最优
方法 2：最小化重投影误差
目标函数：
$\min_X \sum_i |u_i - \pi(P_i X)|^2$
非线性
通常用：
- Gauss–Newton
- Levenberg–Marquardt
Bundle Adjustment 的基本单元
Standard vs General Stereo
| 项目 | Standard Stereo | General Stereo |
|---|---|---|
| 相机结构 | 平行、已校正 | 任意 |
| 搜索维度 | 1D（行） | 2D / 极线 |
| 计算复杂度 | 低 | 高 |
| 精度 | 中 | 高 |
| 应用 | 工程实时系统 | SfM / 多视角 |
为什么两条射线通常不相交？
因为像素噪声和标定误差。
为什么要最小化重投影误差？
因为这是几何上最有意义的误差。
Triangulation 能恢复绝对尺度吗？
不能，
除非基线尺度已知。
一句话总结
Triangulation 是通过多视角射线的几何关系，
恢复 3D 点的位置；
标准立体是其简化版本。
Stereo Vision for Planar Motion
平面运动约束下的立体视觉
什么是 Planar Motion？
相机运动被限制在一个平面内，通常是假设车辆在平坦地面上运动。
典型场景：
- 自动驾驶
- 车载双目相机
- 机器人在地面行走
Planar Motion 的几何约束
在最常见的“道路场景”假设下：
地面是一个平面
相机高度固定
相机：
- 只允许在平面内平移
- 只允许绕垂直轴旋转（yaw）
这会极大减少自由度
一般立体 vs 平面运动立体
一般情况（General Stereo）
- 旋转：3 DoF
- 平移：3 DoF
共 6 DoF
平面运动（Planar Motion）
平移：
- x（前后）
- y（左右）
旋转：
- 1 个角度（yaw）
只剩 3 DoF
为什么 Planar Motion 很重要？
自由度越低，估计越稳定。
具体好处：
- 更少的参数
- 对噪声更鲁棒
- 可以用更少的点
Planar Motion 下的几何关系
核心思想
由于运动受限，极几何不再是完全一般的形式。
结果：
- Essential matrix / Fundamental matrix
→ 结构被简化 - 参数更少
- 估计问题更容易
与 Homography 的关系
Planar Motion 和 Homography 是一回事吗？
不是。
解释：
Homography：
- 假设 场景是平面
Planar Motion：
- 假设 相机运动在平面内
- 场景仍然是 3D
两个“平面”含义不同
在 Planar Motion 下：
相机位姿可以用：
- 一个旋转角
- 一个平移方向（或两个分量）
来表示
因此：
Essential matrix 中：
- 很多元素不再独立
可以用 更少参数 表示
实际应用中的好处
在车载立体视觉中
- 深度估计更稳定
- 位姿估计更可靠
- 对错误匹配不那么敏感
为什么在自动驾驶中常用 Planar Motion 假设？
因为道路近似平坦，
可以显著降低问题复杂度。
Planar Motion 下还能恢复尺度吗？
不能，仅靠视觉仍然有尺度歧义，
除非引入额外信息（轮速、IMU）。
Planar Motion 适合哪些场景？
地面移动平台，
不适合无人机等 6DoF 场景。
平面运动立体视觉利用运动约束，
用更少自由度描述相机关系，
从而提高估计稳定性。
Tomasi-Kanade Factorization
因式分解法的多视角重建
在正交或弱透视相机模型下，多视角 3D 重建可以被转化为一个低秩矩阵分解问题。
Tomasi–Kanade 想解决什么问题？
已知：
- 同一组 3D 点
- 在 多帧图像中被持续跟踪
- 得到大量 2D 观测
目标：
同时恢复相机运动 + 3D 结构
而且：
- 不做两两 stereo
- 一次性用所有视角
核心假设
Tomasi–Kanade 只能在以下相机模型下成立：
- Orthogonal projection（正交投影）
- Weak-perspective projection（弱透视）
不适用于真实透视相机
因为透视投影是非线性的，无法直接形成低秩线性结构。
Measurement Matrix W（核心构造）
假设：
- F 帧
- P 个点
每帧提供：
- x、y 两个坐标
把所有观测堆起来：
尺寸：(2F) × P
最关键的结论
在无噪声情况下，W 的秩 ≤ 3
为什么？
- 每个 3D 点只有 3 个自由度
- 正交 / 弱透视投影是线性的
因式分解的基本形式
$W = M S$
M（Motion matrix）：(2F × 3)
- 描述每一帧的相机姿态
S（Structure matrix）：(3 × P)
- 描述 3D 点坐标
这一步是 代数上的分解
Multi-view reconstruction by orthogonal camera model
正交相机下的因式分解
正交投影下的前处理
去中心化（centering）
把每一帧的点云质心移到原点
原因：
正交投影模型假设：
- 相机原点在点集中心
操作：
- 每一行减去均值
- 得到中心化矩阵 $\tilde{W}$
SVD 分解
对 $\tilde{W}$ 做 SVD：
$\tilde{W} = U \Sigma V^T$
- 只保留 最大的 3 个奇异值
- 得到：
$\tilde{W} \approx U_3 \Sigma_3 V_3^T$
初始因式分解
定义：
- $M_{\text{aff}} = U_3 \Sigma_3^{1/2}$
- $S_{\text{aff}} = \Sigma_3^{1/2} V_3^T$
这是一个 仿射解（affine reconstruction）
仿射歧义
关键问题：
这个分解 不是唯一的
因为：
$W = M S = (M Q^{-1})(Q S)$
其中：
- (Q)：任意 3×3 可逆矩阵
这叫 Affine ambiguity
如何消除歧义？（正交模型）
关键约束
在正交投影下：
相机旋转向量：
- 单位长度
- 相互正交
这些约束 →
对 (Q Q^T) 形成 线性方程组
解 Q 的方法
- 写出正交约束
- 得到一个 过定的线性系统
- 用 最小二乘 / SVD 解
- 从 (Q Q^T) 恢复 (Q)
得到真正的：
- 运动 M
- 结构 S
Multi-view reconstruction by weak-perspective camera model
弱透视模型
为什么要弱透视？
正交投影太理想化，弱透视更接近真实相机。
弱透视 vs 正交的区别
正交：
- 单位长度约束
弱透视：
- 两行长度相等
- 但不一定等于 1
对因式分解的影响
分解步骤 完全一样
区别只在：
- 消除仿射歧义时的约束不同
弱透视约束：
两个方向向量：
- 正交
- 长度相等
| 项目 | Orthogonal | Weak-perspective |
|---|---|---|
| 投影假设 | 理想 | 更真实 |
| 线性 | ✔ | ✔ |
| 可分解 | ✔ | ✔ |
| 适用范围 | 远景 | 中远景 |
优点
- 一次性利用多视角
- 全局一致
- 数学结构清晰
- 速度快（SVD）
缺点
- 必须跟踪点
- 不适合透视投影
- 对 missing data 敏感（后面有扩展）
为什么秩是 3？
因为 3D 点只有 3 个自由度，
投影是线性的。
Tomasi–Kanade 能直接用于真实相机吗？
不能，需要正交或弱透视假设。
结果是唯一的吗？
否，有仿射歧义，需要额外约束消除。
一句话总结
Tomasi–Kanade 把多视角重建转化为低秩矩阵分解问题，
在简化相机模型下可高效恢复结构和运动。
Reconstruction by Merging Stereo Reconstructions
通过合并多次立体重建实现整体重建
每一对相机可以做一次 stereo 得到局部 3D 点云，但它们在不同坐标系下，需要对齐并合并。
为什么需要 Merging？
多个 stereo 对：
- (Image 1, Image 2)
- (Image 2, Image 3)
- (Image 3, Image 4)
每一对都能 triangulation → 3D 点云
但问题是：
每个点云都有自己的坐标系
合并的本质问题
这是一个点集配准（point set registration）问题。
也就是说：
已知：
- 点集 ${p_i}$
- 点集 ${q_i}$
它们表示 同一组物理点
但：
- 坐标系不同
为什么是 Similarity Transformation？
单个 stereo 重建的特点：
- 旋转：确定
- 平移方向：确定
- 尺度：不确定
所以只能用：
$q_i = s R p_i + t$
其中：
- $R$：旋转
- $t$：平移
- $s$：尺度
这就是 Similarity transformation
Similarity Transformation 的自由度
- 旋转：3
- 平移：3
- 尺度：1
共 7 DoF
Registration of two point sets by a similarity transformation
给定：
两组点：
- ${p_i}$
- ${q_i}$
已知一一对应关系
目标：
$\min_{s,R,t} \sum_i |q_i - (sRp_i + t)|^2$
最小二乘意义下的最优对齐
解法的核心思想
先对齐质心，再对齐方向，最后调整尺度。
Step 1：去中心化（消除平移）
计算质心：
$\bar{p},; \bar{q}$
定义：
$p’_i = p_i - \bar{p},\quad q’_i = q_i - \bar{q}$
此时平移已经被“拿掉”
Step 2：估计旋转 R（最关键）
构造协方差矩阵：
$H = \sum_i q’_i p’^T_i$
对 H 做 SVD：
$H = U \Sigma V^T$
得到：
$R = V U^T$
如果 det(R) < 0，需要修正符号
Step 3：估计尺度 s
$s = \frac{\sum_i q’^T_i R p’_i}{\sum_i p’^T_i p’_i}$
直觉：
匹配点间的平均长度比例
Step 4：估计平移 t
$t = \bar{q} - s R \bar{p}$
这是一个“闭式解”的原因
- 不需要迭代
- 不需要初始化
- 全局最优（在最小二乘意义下）
在多视角重建中的使用方式
先做多次 stereo →
得到多个局部点云 →
用 similarity registration 把它们拼接 →
得到整体 3D 结构 →
再用 Bundle Adjustment 精化
为什么不用刚体变换？
因为单次 stereo 重建没有绝对尺度。
至少需要几个点？
至少 3 个非共线点。
如果对应关系有错误怎么办？
实际中会用 RANSAC + registration。
一句话总结
合并立体重建的核心是：
在存在尺度不确定性的情况下，
用相似变换对齐多个 3D 点云。
Numerical Optimization
数值优化就是：用迭代的方法，最小化一个误差函数。
在 3D 视觉里，这个误差通常是：
重投影误差（reprojection error）
为什么需要 Numerical Optimization？
前面的方法有什么问题？
Homography / F / E / Triangulation
大多是线性、闭式解它们：
- 忽略真实几何误差
- 对噪声近似处理
线性解给的是“初值”，不是最优解。
视觉中的典型优化问题
通用形式
$\min_\theta \sum_i | r_i(\theta) |^2$
$\theta$：未知参数
- 相机参数
- 3D 点坐标
$r_i$：残差（误差）
这是一个 非线性最小二乘问题
什么是 Residual（残差）？
残差 = 观测到的像素位置 − 当前模型预测的位置
例如：
- 已知 3D 点 X
- 已知相机参数
- 投影得到 $\hat{u}$
- 实际观测是 $(u)$
残差：
$r = u - \hat{u}$
为什么是“非线性”？
透视投影里有除以 Z。
所以：
- 误差函数对参数是非线性的
- 不能一次解出来
- 只能迭代逼近
优化的基本思想
从一个初始值出发，
沿着“误差下降最快”的方向走，
直到收敛。
梯度、Jacobian、Hessian
Gradient（梯度）
- 指向误差增长最快的方向
- 反方向 = 下降最快
Jacobian（雅可比矩阵）
残差对参数的一阶导数
描述：
“参数改一点，误差变多少”
Hessian（海森矩阵）
- 二阶信息
- 描述误差曲率
在实践中：
- Hessian 太贵
- 通常用近似
最常见的三种优化方法
Gradient Descent（梯度下降）
最简单，但收敛慢。
特点：
- 只用一阶信息
- 对步长敏感
- 很少单独用于 BA
Gauss–Newton（高斯–牛顿）
专门为最小二乘设计的方法。
核心思想：
忽略 Hessian 中的二阶残差项
用：
$H \approx J^T J$
优点：
- 比梯度下降快
- 在误差较小时非常有效
Levenberg–Marquardt（LM）
Gauss–Newton + Gradient Descent 的折中。
更新公式：
$(J^T J + \lambda I)\Delta = J^T r$
直觉解释：
- $\lambda$ 大 → 像梯度下降（稳）
- $\lambda$ 小 → 像 Gauss–Newton（快）
Bundle Adjustment 的标准算法
为什么需要“初始值”？
非线性优化只能保证“局部最优”。
所以：
初始值来自：
- 线性估计
- Triangulation
- Tomasi–Kanade
- Stereo reconstruction
优化什么时候会失败？
- 初始值太差
- 噪声太大
- outliers 没去掉
- 模型不正确
RANSAC 通常在优化之前
为什么视觉里几乎都是最小二乘？
因为噪声通常假设为高斯分布。
Gauss–Newton 做了什么近似？
忽略了残差的二阶导数项。
LM 的 λ 是干什么的？
控制稳定性和收敛速度的权衡。
一句话总结
数值优化是用迭代方法最小化重投影误差，
LM 是多视角重建中最核心的优化工具。
Numerical Multi-view Reconstruction
Bundle adjustment
束调整
Bundle Adjustment 是同时优化所有相机参数和所有 3D 点，使总重投影误差最小。
更口语一点：
让所有相机看到的所有点，在图像中“对得最齐”。
为什么叫 “Bundle”？
每一个 3D 点 + 相机中心
形成一束投影光线（bundle of rays）
Bundle Adjustment：
同时调整这些“光线束”的交点位置。
BA 在整个流程中的位置
特征匹配 →
RANSAC 估计 F / E →
分解得到相机位姿 →
Triangulation 得到 3D 点 →
Bundle Adjustment 全局优化
BA 不是起点，是“精修”
BA 优化的是什么？
优化变量（θ）
所有相机参数：
- 旋转 R
- 平移 t
- （可能还有内参）
所有 3D 点坐标：
- $X_j$
优化目标函数
$$ \min_{{R_i,t_i,X_j}} \sum_{i,j} |u_{ij} - \pi(R_i,t_i,X_j)|^2 $$解释：
- $u_{ij}$：第 i 个相机观测到第 j 个点的像素
- $\pi$：投影函数
- 误差 = 重投影误差
为什么 BA 是“非线性 + 大规模”的？
非线性
- 透视投影里有除法
- 旋转参数本身是非线性的
大规模
20 个相机，1000 个点
参数数 ≈ 20×11 + 1000×3 ≈ 3000+
Hessian 是 3000×3000
直接求逆几乎不可行
BA 用什么算法？
Levenberg–Marquardt（LM）
原因：
- 专为非线性最小二乘设计
- 比 Gauss–Newton 更稳定
BA 的关键计算结构
Jacobian 矩阵的特点
极其稀疏（sparse）
原因：
每个残差：
- 只和 一个相机
- 和 一个 3D 点
有关
利用稀疏结构做什么？
Schur Complement
先消掉 3D 点变量，
只在相机参数空间里求解，
再反推出 3D 点更新。
结果：
- 大矩阵 → 小矩阵
- 计算量大幅降低
- 数值更稳定
这是 BA 能跑起来的关键
输入
- 初始相机参数
- 初始 3D 点
- 特征匹配关系
输出
- 优化后的相机位姿
- 优化后的 3D 结构
整体最优（局部意义下）
优点
- 精度最高
- 全局一致
- 理论严谨
缺点
- 计算量大
- 需要好初值
- 对 outliers 敏感（通常已用 RANSAC 处理）
为什么 BA 不能从零开始？
因为是非线性优化，
容易陷入错误的局部最优。
BA 会改变相机内参吗？
可以，
取决于是否把内参作为变量。
BA 和 Triangulation 的关系？
Triangulation 是局部解，
BA 是全局优化。
一句话总结
Bundle Adjustment 是多视角重建中
最终、最精确的全局优化步骤，
通过最小化重投影误差联合优化相机和结构。
Reconstruction by Special Devices
利用特殊传感器进行三维重建
特殊设备不是“看”，而是“直接量距离”。
与普通相机的本质区别：
- 相机：间接恢复深度（靠几何）
- 特殊设备：直接测深度
Laser scanning
激光扫描
发射一束激光，等它反射回来，用时间或相位差算距离。
基本原理
发射激光
激光击中物体
反射回传感器
测量：
- Time-of-Flight（飞行时间）
- 或 相位差
距离：
$d = \frac{c \cdot \Delta t}{2}$
得到的结果
每一次测量：
- 一个方向
- 一个距离
多次扫描 → 3D 点云
优点：
- 精度高
- 与光照无关
- 几何直接
缺点：
- 扫描慢（机械结构）
- 成本高
- 动态场景困难
典型应用
- 建筑扫描
- 文物数字化
- 工业测量
Depth camera
深度相机
能同时输出 RGB 图像 + 每个像素的深度。
常见实现方式
Structured Light（结构光）
- 投射已知光栅
- 看变形
- 根据变形计算深度
早期 Kinect
Time-of-Flight（ToF）
- 发射红外光
- 测飞行时间或相位差
- 每个像素一个距离
新一代 Kinect、手机 3D 相机
Depth Camera 的输出
- 深度图（Depth map）
- 每个像素都有 Z
直接可转为点云
优点：
- 实时
- 使用简单
- 直接得到深度
缺点：
- 室外容易受干扰
- 测距范围有限
- 深度噪声较大
典型应用
- 手势识别
- 人体重建
- 室内 SLAM
LiDAR
激光雷达
高速、远距离、360° 的激光扫描系统。
工作方式
- 连续发射激光脉冲
- 旋转扫描
- 对每个方向测距
得到：
- 稠密或半稠密 3D 点云
与普通 Laser Scanner 的区别
| Laser Scanner | LiDAR |
|---|---|
| 慢 | 快 |
| 局部 | 大范围 |
| 静态 | 动态也可 |
| 工业 | 自动驾驶 |
优点：
- 远距离
- 高精度
- 不依赖纹理
- 室外稳定
缺点：
- 昂贵
- 数据量大
- 物体表面稀疏
典型应用
- 自动驾驶
- 无人机测绘
- 城市建模
特殊设备 vs 普通视觉
| 项目 | 普通相机 | 特殊设备 |
|---|---|---|
| 深度获取 | 间接 | 直接 |
| 是否需要匹配 | ✔ | ✘ |
| 是否有尺度 | ✘ | ✔ |
| 依赖光照 | ✔ | ✘ |
| 成本 | 低 | 高 |
特殊设备解决的是“深度获取难”的问题，
但代价是成本和复杂度。
为什么还要学多视角视觉？
因为相机便宜、通用、信息丰富，
特殊设备只是补充，不是替代。
LiDAR 和 stereo 谁更准？
LiDAR 深度更准，
stereo 空间分辨率更高。
Depth camera 能完全替代 stereo 吗？
不能，
室外和远距离表现较差。
这些设备还需要 BA 吗？
可以，
尤其在多帧对齐和 SLAM 中。
一句话总结
特殊设备通过主动测距直接获得深度，
与基于几何推断的视觉方法形成互补。
3D Computer Vision